В предыдущем уроке мы с вами освоили основной принцип решения любых дробных уравнений. Это — ликвидация дробей. Кто читал, тот понял, что ничего сложного в этом нет.
Однако, даже в самых простых (казалось бы!) дробных уравнениях нас может поджидать сюрприз не из приятных. С ним, с сюрпризом, надо разобраться! Разберёмся?)
Основная проблема в решении дробных уравнений.
Сейчас мы с вами научимся обходить одну из самых коварных ловушек на ЕГЭ и контрольных! Попадаются в неё все — и троечники и отличники. Я специально поставил её в самое примитивное уравнение, чтобы с ней (с ловушкой) хорошенько разобраться. Но для начала посмотрим, попадёте вы в неё или нет.)
Допустим, надо решить вот такое нехитрое уравнение:
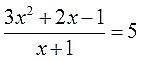
Дело уже привычное и знакомое. Умножаем всё уравнение на знаменатель (х+1) и получаем:
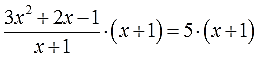
Напоминаю, что со скобками (х+1) работаем целиком, как будто бы это одно число! Производим умножение:
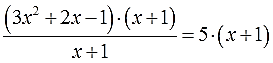
Сокращаем знаменатель и избавляемся от дроби:
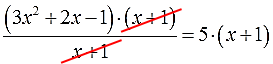
3x2 + 2x — 1 = 5(x+1)
Раскрываем оставшиеся скобки, переносим всё влево, приводим подобные:
3x2 + 2x — 1 = 5x + 5
3x2 - 3x — 6 = 0
Делим всё уравнение на 3 и получаем:
х2 — х — 2 = 0
Отлично. Самое обычное квадратное уравнение. Решаем и получаем два корня:
х1 = -1
х2 = 2
Предположим, в задании на ЕГЭ сказано записать в ответ меньший из корней, если корней более одного. Что писать будем?)
Если вы решили, что ответ -1, то вы попали в ловушку. И задание вам не засчитают, да. Зря старались. Правильный ответ был 2… Два, а не минус один.
Так в чём же дело? А вы попробуйте проверку сделать. Подставьте каждый из найденных иксов в исходное уравнение. И, если при х=2 у вас всё славненько срастётся, получится тождество 5=5, то при х=-1 получится деление на ноль! Чего делать нельзя категорически. Нет такой операции ни в природе, ни в математике…
Что это значит? Это значит, что х=-1 — так называемый посторонний корень. Или лишний корень. Он не является корнем нашего дробного уравнения и в ответе никак не учитывается. Ибо его подстановка даёт бессмыслицу. Его мы просто отбрасываем. Окончательный корень один.
А именно: х=2.
Так, стоп, что-то тут не так! Нам же говорили, что всё уравнение можно умножать на одно и то же выражение! Это же тождественное преобразование!
Да, тождественное. Я не спорю. Но при одном маленьком ограничении, которое многие попросту игнорируют. А именно — выражение, на которое умножаем (делим), отлично от нуля! А скобочка (х+1) при х=-1 обращается в ноль! Так что всё честно.
И что нам теперь делать? Совсем не умножать? Тогда мы вообще ничего не решим! Каждый раз проверку делать? Это с ума сойдёшь. Особенно, если уравнение навороченное.
Нет, мы с вами пойдём красивым и элегантным путём. Обратимся за помощью к трём волшебным буквам! Догадались? Да! Это ОДЗ! Область Допустимых Значений.
Что же такое ОДЗ?
Это такие значения икса, которые могут быть в принципе. Или которые разрешены для данного примера.
Например, в уравнении
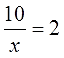
мы ещё пока не знаем, чему равен икс, верно? Мы уравнение пока не решили. Но зато мы железно знаем, что икс не может равняться нулю ни в коем случае! На ноль делить нельзя. На любое другое число — целое, дробное, отрицательное, иррациональное — ради бога. А вот на ноль — никак. Стало быть, в этом примере ОДЗ:
х — любое число, кроме нуля.
Зато все остальные иксы — абсолютно безопасны. Хоть 41, хоть -17, хоть -1,3 — весь бесконечный набор чисел.
Идея ясна?
Как записывать ОДЗ? Как работать с ОДЗ?
Тоже легко. На первом этапе всегда внимательно осматриваем исходный пример и ищем опасные места. Что значит опасные места?
Это места, где возможны запретные действия. Действия, которые при каких-то иксах могут оказаться недопустимыми с точки зрения математики. В нашей теме такое действие всего одно — деление. Нельзя делить на ноль. Есть ещё запреты в корнях чётной степени, в логарифмах и в тригонометрии. Их мы тоже рассмотрим в соответствующих уроках.
Как только опасные места найдены, рядышком с примером выписываем условия, которые не приводят к бессмыслице. После этого, глядя на эти условия, вычисляем запретные иксы. И исключаем их из ОДЗ. Вот и всё.
Я специально акцентирую внимание на словах "исходный пример". Любое преобразование (сокращение, приведение подобных и т.п.) может изменить ОДЗ, и мы можем получить неверный ответ.
Важно! Для поиска ОДЗ мы не решаем пример! Мы решаем всего лишь маленькие кусочки примера для нахождения запретных иксов.
"Многа букаффф", да. Но на практике вся процедура выглядит до ужаса элементарно.
Итак, берём наше уравнение:
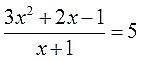
Ничего пока что не трогаем, а внимательно осматриваем исходное уравнение. Осмотрев, мы сразу замечаем операцию деления на х+1.
Это потенциально опасная операция: при каких-то значениях икса выражение х+1 может оказаться равным нулю. На который делить нельзя. Поэтому обезопасим себя вот такой записью:
х+1 ≠ 0
х ≠ -1
Во-о-т. Минус один категорически не подходит нам в качестве ответа. Это и будет ОДЗ для нашего уравнения. Все иксы, кроме минус единички.
На практике запись и нахождение ОДЗ обычно оформляют так:
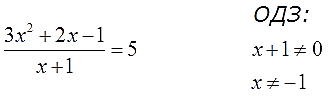
Иногда ОДЗ записывают и в другой форме, через промежутки. Вот так:
x ∈ (-∞; -1) U (-1; +∞)
Читается эта запись так: "Икс принадлежит интервалу от минус бесконечности до минус единицы (не включая), и от минус единицы (не включая) до плюс бесконечности."
Перевод с математического на человеческий: "Икс — любое число, кроме минус единицы."
Вот и всё. Как только мы себя обезопасили такой записью, дальше мы имеем полное право делать с уравнением всё что хотим — переносить члены, домножать, сокращать… Вот и домножаем всё уравнение на (х+1). Дробь-то убирать всё равно надо! Это по-прежнему будет не совсем тождественным преобразованием, но все вредные последствия от нарушения тождественности мы исключим по ОДЗ.
Умножаем:
3x2 + 2x — 1 = 5(x+1)
Как вы думаете, в какой же момент мы с вами попали в ловушку элементарного примера? Как раз в момент домножения всего уравнения на знаменатель дроби! Знаменатель исчез, и вместе с ним исчезли и соответствующие ограничения на иксы. Бесследно. И для нового уравнения, без дроби, на икс уже не накладывается никаких запретов! Любым может быть икс…
В математике это явление называется расширение ОДЗ.
Но теперь мы уже с вами народ бдительный. Исходные ограничения (х≠-1) мы записали и сохранили.
Поэтому дальше спокойно решаем уравнение безо всяких дробей и получаем два корня:
х1 = -1
х2 = 2
А вот теперь стыкуем наши результаты и условия ОДЗ. И видим в наших кандидатах на ответ один из иксов в качестве запретного! Минус один. Это означает, что в окончательный ответ его включать нельзя. Это посторонний корень, появившийся в процессе решения без нашего желания.
Да, это законный корень нашего вспомогательного квадратного уравнения, но никак не корень исходного дробного уравнения!
Стало быть, минус единицу мы безжалостно вычёркиваем и в ответ не включаем. Вот и всё.)
А в других уравнениях прошлого урока? Там что, нет ОДЗ? Есть, разумеется. Есть деление на икс — есть и ОДЗ.
В первом уравнении:
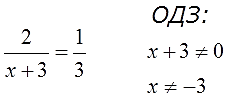
Во втором уравнении:
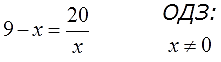
И так далее.
Я специально в тех примерах ничего не сказал про ОДЗ. Чтобы вас не перегрузить раньше времени.) В всех уравнениях прошлого урока (и домашнего задания к нему) ОДЗ никак не сказывалась на ответе. Так бывает. Но в заданиях ОГЭ и ЕГЭ ОДЗ в 99% случаев влияет на ответ! Так что мы с ОДЗ дружить будем. И во всех темах, где это необходимо, мы будем про ОДЗ вспоминать. Чтобы не упасть лицом в грязь.)
Итак, про ОДЗ поговорили. Убедились, что работать с ней тоже совсем не сложно. Теперь можно перейти и к общему алгоритму решения любого дробного уравнения.
Решаем дробные уравнения по алгоритму!
Для успешного решения любого дробного уравнения необходимо выполнить (правильно) пять пунктов:
1. Разложить знаменатели всех дробей на множители (если требуется). До упора. Переписать уравнение с учётом этого факта.
2. Найти ОДЗ, записать рядышком с уравнением и временно (до конца решения) забыть про неё.
3. Сообразить, на что надо умножить обе части уравнения, чтобы все дроби исчезли полностью.
4. Выполнить это самое умножение и решить новое уравнение, уже безо всяких дробей. Найти решения (кандидаты в ответ).
5. Вспомнить про ОДЗ и состыковать найденные решения с условиями ОДЗ. Те решения, которые не входят в ОДЗ, безжалостно выбросить. Записать окончательный ответ.
А теперь, вооружившись таким мощным супероружием, как ОДЗ, и общим алгоритмом, разберём очередной пример. Супердетально разберём!
Решить уравнение:
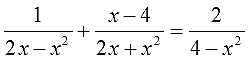
Решаем строго по пунктам. Выполняем пункт первый:
1. Разложить все знаменатели на множители (если требуется). До упора. Переписать пример с учётом этого факта.
Знаменатели наших дробей НЕ разложены на множители. Вот и приступаем. Вынесение общего множителя за скобки и формула разности квадратов — мощные штуки.)
2x — x2 = x(2-x)
2x + x2 = x(2+x)
4 — x2 = 22 — x2 = (2-x)(2+x)
Вот так. А теперь переписываем уравнение с учётом наших разложений:
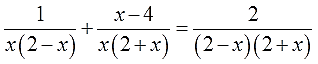
Готово. Все знаменатели разложены до упора.) Можно приступать ко второму пункту.
2. Найти ОДЗ, записать рядышком с примером и временно (до конца решения) забыть про неё.
Итак, начинаем осматривать исходный пример на наличие опасных операций.
Внимание! Ничего не трогаем и не решаем! Не складываем дроби, не приводим подобные, не сокращаем!!!
Подобные преобразования запросто могут изменить ОДЗ, что может привести к неверному ответу! Оно нам надо?! Ещё раз напоминаю: ДО поиска ОДЗ с исходным примером мы не делаем НИЧЕГО! Кроме разложения на множители. Оно — безопасно и даже полезно.)
Берём и именно осматриваем исходный пример. И замечаем три опасных места: каждая из дробей таит в себе возможное деление на ноль.
Вот и пишем:
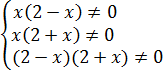
Знак системы (фигурная скобка) здесь не зря поставлен. Она означает, что все три условия должны выполняться одновременно! Мы ведь ОДЗ записываем не для каждой дроби по отдельности, а для всего примера целиком.)
Ну и как? Нашли ОДЗ? Не-а…)
Мы записали кусочек примера, записали три требования, которые должны выполняться железно. Но этого мало. Нужно ещё найти иксы, которые обеспечивают эти железные требования. ОДЗ ведь к иксам относится, а не к кусочкам примера…
Как же найти значения иксов, которые не превращают знаменатели дробей в ноль? Их же очень много? Очень просто! Мы поступим элегантно. Найдём иксы, которые наоборот, превращают знаменатели дробей в ноль. Это и будут запретные иксы.
Вот и решаем эти неравенства методом "от противного". То есть, делаем из неравенств уравнения:
x(2-x) = 0
x(2+x) = 0
(2-x)(2+x) = 0
Именно из этих трёх уравнений мы и будем искать запретные иксы. Уравнения очень простые: произведение равно нулю, когда хотя бы один из множителей равен нулю. Вот и приравниваем (в уме или на черновике) каждый множитель к нулю.
Для первого уравнения получаем: x1 = 0; x2 = 2.
Вспомнив, что это запретные иксы, получим:
х ≠ 0; x ≠ 2.
Точно так же решаем и два оставшихся уравнения.
Для второго уравнения получаем:
x ≠ 0; x ≠ -2.
И, наконец, для третьего уравнения получаем:
x ≠ 2; x ≠ -2.
Видно, что некоторые запретные значения иксов повторяются. Разумеется, для окончательной записи ОДЗ мы их не будем дублировать. Итого ОДЗ для нашего уравнения будет выглядеть вот так:
ОДЗ:
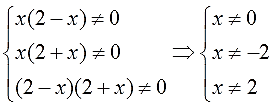
Видите, насколько полезно предварительно раскладывать знаменатели на множители! В уме ОДЗ ищется! Поэтому эта процедура и стоит первым пунктом в алгоритме.)
Можно приступать к третьему пункту.
3. Сообразить, на что надо умножить обе части уравнения, чтобы все дроби исчезли полностью.
И тут разложение на множители тоже здорово играет на руку!
Понятно, что для ликвидации первой дроби, надо её домножать на x(2-x), вторую — на x(2+x) и третью - на (2-x)(2+x).
Но чтобы сразу сократить все дроби, надо скомбинировать такое выражение, которое одинаково хорошо делится и на х(2-х), и на х(2+х), и на (2-х)(2+х).
Вот оно, это выражение:
х(2-x)(2+x)
Как же я до него додумался? Очень просто: составил произведение всех неповторяющихся множителей всех знаменателей. Чтобы ничего не забыть и лишнего не взять.) Приступаем к четвёртому пункту:
4. Выполнить это самое умножение и решить новое уравнение, уже безо всяких дробей. Получить решения (кандидаты в ответ).
Итак, умножаем:
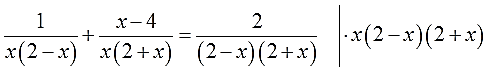
И снова, чтобы не заплутать в трёх соснах, используем скобки:
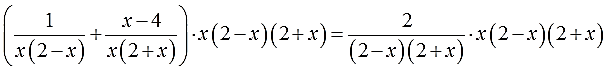
Производим умножение. Большие скобки раскрываем, малые — не трогаем!
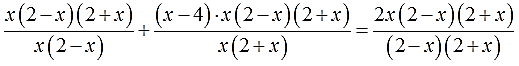
Сокращаем все дроби:
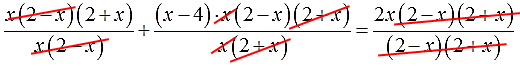
2 + x + (x-4)(2-x) = 2x
Всё. От дробей избавились. Как обычно, раскрываем оставшиеся скобки, приводим подобные и собираем все члены слева:
2 + x + 2x — x2 — 8 + 4x — 2x = 0
–х2 + 5x — 6 = 0
Помним, что минус впереди крайне неудобен, посему умножаем всё на (-1):
x2 — 5x + 6 = 0
Решаем простенькое квадратное уравнение и получаем корни:
x1 = 2
x2 = 3
Нашли кандидатов в ответ. Самое время вспомнить про ОДЗ. Про самый последний пункт:
5. Вспомнить про ОДЗ и состыковать найденные решения с условиями ОДЗ. Те решения, которые не входят в ОДЗ, безжалостно выбросить. Записать окончательный ответ.
Итак, наши решения:
x1 = 2
x2 = 3
Условия ОДЗ:
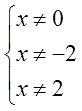
Сопоставляем и… Оп-па! А ведь двойка — запретное значение! Нас не проведёшь! ОДЗ — штука жёсткая. В отвал двойку!
Окончательный ответ: х = 3.
Именно так и решаются все дробные уравнения. В пять шагов. Зачем же я распинался, рассказывая целый урок про избавление от дробей, затем ещё пол-урока про ОДЗ? Мог бы сразу дать общий алгоритм и соответствующий пример!
На этот вопрос отвечу так. Если бы вы знали, сколько народу спотыкается на применении тупо заученного алгоритма! А уж при малейшем отклонении от шаблона простой пример становится вообще нерешаемым… Если понимать смысл, то шанс решить есть всегда. Понимание всегда побеждает механическую память.)
Вот, собственно, и всё, что я хотел сказать. И напоследок очередная порция примеров для самостоятельного решения.
Решить уравнения:
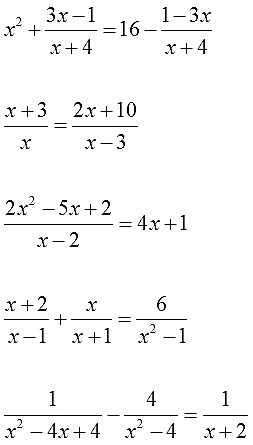
Ответы (по традиции, в беспорядке):
x = 3
x = -1
x = 4
x1 = -1; x2 = -9
x = -2
Всё совпало! Поздравляю! У вас иксов побольше будет? Хм… Про ОДЗ не забыли, случаем? Кое-какие корни выбрасывать надо! ОДЗ учли, а всё равно не выходит? Да-а-а… Проблемка. Такие уравнения надо уметь решать: слишком уж они популярны во многих темах математики. Особенно — в текстовых задачках! Но не отчаивайтесь!
Перечитайте этот и предыдущий уроки ещё раз и прогуляйтесь по смежным темам: разложение на множители, квадратные уравнения, линейные уравнения и (особенно!) тождественные преобразования уравнений. И всё получится. Я в вас верю!)
