И снова приветствую всех тех, кто серьёзно готовится к профильному ЕГЭ и всерьёз претендует на решение самых сложных задач 19 (они же С6)! Как и обещал, продолжаем разбирать самые разнообразные и необычные задачи на теорию чисел и способы успешно расправляться с такими монстрами. Хотя для подготовленного ученика в задачах 19 страшного особо ничего и нету.)
Использование признаков делимости и перебора на ограниченном множестве. Задача про числа-палиндромы.
В данном материале я хотел бы разобрать очередную необычную и не самую сложную задачку про так называемые числа-палиндромы. Для начала, что это вообще за зверь такой (для тех, кто не в курсе)?
Палиндром — это слово, число или даже целый текст, одинаково читающееся в обоих направлениях. Как слева направо, так и справа налево.
Примеры:
Число 12321, слово «ротор», красивое женское имя Анна, словосочетание «искать такси», а также всем известная бородатая фраза «А роза упала на лапу Азора». В общем, идея понятна, я думаю. :)
В нашей задаче, разумеется, речь пойдёт о числах. Что ж, давайте теперь посмотрим на саму задачу.

Вот такая вот задачка. Как к ней подступиться? Ну, во-первых, в каждом из пунктов речь идёт о делимости на 15. Стало быть, нашей отправной точкой будут признаки делимости чисел нацело. Это тема 6-го класса средней школы. Других вариантов просто нет. И какие же это признаки, спросите вы?
Вспоминаем 6-й класс, ищем там признак делимости на 15 и… вы правы! Такого признака нету. Но! Зато есть признаки делимости чисел на 3 и на 5. А что такое 15? Это не что иное, как 3·5! Элементарно, Ватсон! :) Стало быть, если какое-либо натуральное число одновременно делится нацело на тройку и пятёрку, то автоматически оно будет делиться и на пятнадцать. Поэтому давайте-ка быстренько освежим в памяти признаки делимости чисел на 3 и на 5. Вот они:
Признак делимости на 3
Натуральное число делится нацело на 3, если сумма его цифр делится на 3.
Скажем, число 12384 точно поделится на 3, так как сумма его цифр 1+2+3+8+4 = 18 делится на 3. А вот 23576 даже и пытаться не стоит, так как его сумма цифр 2+3+5+7+6 = 23 не делится на 3.
Признак делимости на 5
Натуральное число делится нацело на 5, если оно заканчивается цифрой 0 или 5.
Например, на 5 делится число 12345, так как оно заканчивается на пятёрку. Или 1234567890, так как оно заканчивается нулём. Ну, в общем, вы поняли. Признак очень простой.
Значит, натуральное число делится на 15 тогда и только тогда, когда оно одновременно делится на 3 (по сумме цифр) и на 5 (по последней цифре). Что ж, теоретическая база подготовлена, пора приступать к разбору нашей задачи. Итак,
а) Приведите пример числа-палиндрома, который делится на 15.
Прежде чем что-то решать, давайте посмотрим, как вообще устроены числа-палиндромы:

И так далее…
Здесь a, b, c и так далее — цифры натурального числа. В общем случае — различные. Черта сверху ставится для того, чтобы обозначить тот факт, что перед нами именно цифры, а не произведение типа a·b·c.
Скажем, запись
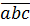
означает трёхзначное натуральное число, которое в десятичной форме запишется так:
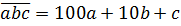
Что ж, давайте теперь искать числа-палиндромы, делящиеся на 15. Для начала поищем их среди двузначных чисел. Это числа 11, 22, 33, 44 и так далее до 99. Можно заметить, что все они делятся на простое число 11:
11=11·1
22=11·2
33=11·3
И так далее. Наименьшее число, которое делится как на 11, так и на 15 — это 11·3·5 = 165 - уже трёхзначное. Облом. Значит, среди двузначных чисел таковых нету.
Что ж, поехали шерстить трёхзначные числа. :) Трёхзначное число-палиндром имеет вид
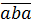
Раз оно делится на 15, то должно делиться как на 5 (по последней цифре), так и на 3 (по сумме цифр).
Значит, согласно признаку делимости на 5, последняя цифра (a) может быть только 0 или 5. Третьего не дано. :)
А теперь прикинем. Если a = 0, то наше число имеет вид
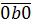
и никак не является трёхзначным. Значит, единственный устраивающий нас вариант - это
а = 5.
Поэтому трёхзначные числа-палиндромы, делящиеся на 5, имеют вид:
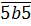
Что ж, кое-чего уже проясняется. :)
А теперь в игру дополнительно вступает признак делимости на 3. Составляем сумму цифр:
5 + b + 5 = 10 + b,
где b, будучи цифрой числа, принимает значения 0, 1, 2, 3, …, 9.
Теперь понятно, как расправиться с пунктом а). Подберём число b так, чтобы выражение для суммы цифр 10 + b делилось бы на 3. Например, при b = 2 получим:
10+b = 10+2 = 12 — делится на 3.
Следовательно, самое первое по счёту трёхзначное (и вообще глобально) число-палиндром, делящееся на 15, - это число 525.
Всё, этого вполне достаточно для ответа на вопрос пункта а).
Ответ: Например, 525.
Переходим к пункту б).
б) Сколько существует пятизначных чисел-палиндромов, делящихся на 15?
Все пятизначные числа-палиндромы имеют вид:
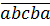
Здесь снова рулят признаки делимости чисел на пятёрку и на тройку. Как и в предыдущем пункте, начнём с признака делимости на 5. Это означает, что последняя цифра в нашем числе (т.е. а) может быть равна либо нулю, либо пятёрке.
Нулём цифра а быть никак не может, поскольку в таком случае наше число примет вид
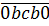
и попросту не будет пятизначным. Значит, а = 5 (и только 5).
Итак, наши пятизначные кандидаты предварительно обретают вот такой вид:
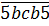
Теперь снова подключаем признак делимости чисел на 3 по сумме цифр. В нашем случае:
5 + b + c + b + 5 = 10 + 2b + c — должно делиться на 3.
В предыдущем пункте мы варьировали только одну единственную цифру b, добиваясь делимости на 3 суммы цифр (напомню, это было выражение 10+b). Здесь же нам надо варьировать уже две цифры — b и c. И как нам теперь быть? Ведь число всевозможных вариантов стало гораздо больше! Да, не спорю, больше. На первый взгляд может показаться, что вариантов и вправду довольно много и перебирать их все очень долго и муторно. Но давайте подумаем: ведь b и с — не просто числа, а цифры натурального числа. Которые могут принимать очень ограниченные значения — 0, 1, 2, 3, …, 9. Поэтому, если мы как-то зафиксируем b, последовательно придавая ему значения от 0 до 9, то в каждом из случаев варьировать уже придётся только одну цифру c. Давайте посмотрим, как это делается. Первый случай я разберу подробно, а остальные — кратко.
Итак, первый вариант b = 0. Тогда сумма цифр 10 + 2b + c нашего числа будет равна:
10+2·0+c = 10+c.
Когда выражение 10+c делится на 3? Очевидно, в трёх ситуациях:
10+c = 12 (тогда c = 2),
10+c = 15 (тогда c = 5),
10+c = 18 (тогда c = 2).
Всё. Больше, чем 8 (например, 11) число с быть уже никак не может. Ещё раз напоминаю, что наши буковки — это на самом деле циферки. :) То есть, 0, 1, 2, …, 9. Этот случай дал нам три пятизначных числа-палиндрома делящихся на 15. Какие же это числа? Пожалуйста, вот они:
50205, 50505 и 50805 (3 числа).
Пусть теперь b = 1. В этом случае сумма цифр нашего числа будет такая:
10+2·1+c = 12+c
Добиваясь теперь, чтобы выражение 12+c делилось на 3, получим с = {0; 3; 6; 9}. Итого выплыли ещё 4 числа-палиндрома (51015, 51315, 51615, 51915).
Уловили закономерность? :) Да! Надо разобрать оставшиеся 8 случаев. Не так уж и много, по большому счёту. Добрый вечер! Буду краток. :)
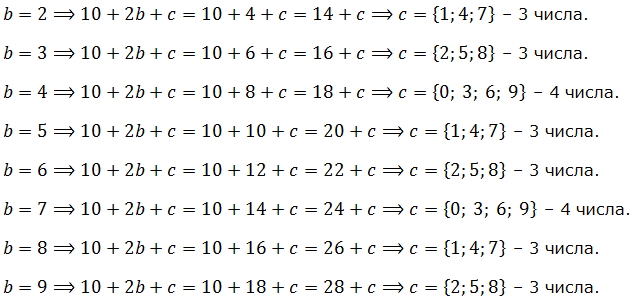
Подобная процедура в целочисленных задачах называется перебор на ограниченном множестве. Суть метода заключается в том, что, если число всевозможных вариантов не очень большое (в нашем случае — всего 10), то мы просто перебираем все-все возможные случаи и отбираем всё то, что нас устраивает. :)
А теперь подсчитываем наших цыплят палиндромов:
3 + 4 + 3 + 3 + 4 + 3 + 3 + 4 + 3 + 3 = 33
Итого тридцать три коровы пятизначных числа-палиндрома, делящихся на 15! :)
Ответ: 33.
Теперь, когда проведено столь масштабное исследование, самый сложный пункт в) многим ученикам может показаться совсем пустяковым. :) Сейчас всё увидите!
в) Найдите 37-е по величине число-палиндром, которое делится на 15.
Для ответа на вопрос сначала подсчитаем все трёхзначные и четырёхзначные числа-палиндромы.
Одно из трёхзначных (самое первое вообще среди таких чисел) мы уже нашли — это 525. Давайте найдём все остальные. Для этого снова обратимся к нашей сумме цифр (см. пункт а)):
10 + b – делится на 3.
Тогда b = {2; 5; 8} — три трёхзначных числа-палиндрома (т.е. 525, 555 и 585).
Разбираемся теперь с четырёхзначными числами-палиндромами. Здесь всё аналогично. Они имеют вот такую запись:
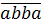
По признаку делимости на 5, последняя (и первая) цифры могут быть равны 0 или 5. Сразу, по понятным причинам, отметаем ноль и получаем:
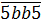
По признаку делимости на 3 составляем сумму цифр:
5 + b + b + 5 = 10 + 2b.
Чтобы эта штука делилась на 3, цифра b должна принимать лишь одно из трёх значений: b = {1; 4; 7}. Итого получаем три четырёхзначных числа-палиндрома (5115, 5445 и 5775).
Тогда получается, что всего трёх-, четырёх- и пятизначных чисел-палиндромов, делящихся на 15, будет:
3 (трёхзначные)+3 (четырёхзначные)+33 (пятизначные) = 39 чисел.
Тогда очевидно, что искомое 37-е число-палиндром — пятизначное. Гуд.) Идём дальше.
А теперь смотрим на результаты нашего исследования пятизначных чисел в пункте б). Я не стал для каждого случая выписывать их все, но зато можно заметить, что при росте b все наши получаемые числа располагаются в порядке возрастания. Это значит, что самое последнее, 39-е число будет соответствовать случаю b=9, c=8. Тогда искомое 37-е по величине число-палиндром, делящееся на 15, будет соответствовать случаю b=9, c=2, т.е. 59295.
Вот и всё! :)
Ответ: 59295.
Как видите, ничего сложного. Если знать пару признаков делимости и понимать суть задания (что такое число-палиндром и немного что такое десятичная запись числа). Да, в пункте б) надо разбирать 10 случаев, но все они совсем простые и решаются фактически в уме. Главное — не бояться!
