Формула суммы n первых членов геометрической прогрессии ни по виду, ни по смыслу, ничуть не сложнее аналогичной формулы для арифметической прогрессии. Почитайте, кстати, кто забыл.)
Для геометрической прогрессии формула суммы выглядит вот так:
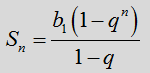
Смысл формулы суммы тот же самый: она позволяет быстро подсчитывать результат сложения всех членов геометрической прогрессии с первого по последний. Если таких членов мало, то можно и на бумажке всё сложить да посчитать — не проблема. А вот если членов много и (или) числа большие, то сложение в столбик уже напрягает. Тогда только формула, да…
Буковки в формуле:
Sn — сумма членов геометрической прогрессии с первого по последний. Причём, опять же, обращаю ваше внимание, что складываются именно все члены подряд, без пропусков! И именно с первого.
b1 — первый член прогрессии. Здесь всё ясно, никаких фокусов.
q — знаменатель прогрессии. Тоже всё знакомо, ничего хитрого.
n — номер последнего члена. Совпадает с количеством складываемых членов.
На вид всё просто, а вот на практике с записью формулы случаются проблемы. И если с первым членом b1 у народа обычно всё в порядке, его всегда в числитель дроби пишут, то многочисленные разности единички и знаменателя q постоянно путаются в голове. Гораздо чаще, чем хотелось бы… Где и что сидит? 1-q или q-1? (1-qn) или же (1-q)n ? Что сидит в числителе, а что в знаменателе? Это первая (и основная) причина путаницы, а вот вторая.
Дело всё в том, что во многих учебниках формулу суммы частенько пишут немного по-другому. Вот так:
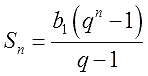
Нашли отличия? Да! И в числителе и в знаменателе единичка и знаменатель поменялись местами.) Но общая суть формулы осталась прежней! Основное свойство дроби помните? Если числитель и знаменатель дроби помножить на одно и то же число, значение дроби не изменится.)
Так и здесь. Если числитель и знаменатель дроби в основной формуле суммы помножить на (-1), то получим вспомогательную формулу:
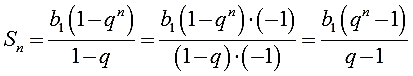
И что же правильно? Всё правильно! И тот и другой варианты записи формулы вполне себе рабочие и имеют право на жизнь. Вот и теряется народ…
Так как же всё-таки запомнить формулу суммы так, чтобы никогда не путаться? Легко! Вот вам краткий алгоритм для запоминания.
На первом этапе определяемся с порядком вычитания — от единички знаменатель отнимать будем (1-q) или же наоборот (q-1). Причём важно: порядок вычитания мы выбираем сами! Как хотим.) Я всё же выберу первый вариант (1-q). Он чуть более предпочтителен для работы с суммой, чем второй. Почему? Об этом в следующем уроке будет.
На втором этапе рисуем черту дроби. И в числитель и в знаменатель пишем разность единички и знаменателя в выбранном порядке! Как сами выбрали, так и пишем. Одинаково и в числитель и в знаменатель! Вот так:
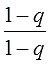
На третьем этапе ещё раз смотрим на формулу. И соображаем, что числитель отличается от знаменателя одной лишь маленькой буковкой – степенью n у знаменателя прогрессии.
Пишем:
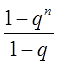
Обращаю ваше внимание, что в степень n возводим не всю разность 1-q целиком, а только знаменатель прогрессии! И именно в числителе. Это важно.
А дальше осталось умножить полученную дробь на первый член (b1). Из действий с дробями вспоминаем, что при умножении дроби на число оно (число) идёт наверх, в числитель. Поэтому при умножении заключаем числитель дроби в скобочки и получаем то что нам нужно:
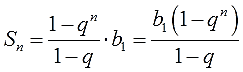
Вот такой простой и безотказный приёмчик. Имеет смысл запомнить эту цепочку. Тогда путаницы и ошибок будет на порядок меньше. Проверено. Помогает.)
Прошу заметить, приведённая цепочка — это всего лишь приём для запоминания формулы, а ни в коем случае не вывод! Выводится эта формула весьма хитро и нетривиально. Но нам ведь не столько вывести саму формулу важно, сколько потренироваться с ней работать, правда?
Решение заданий на формулу суммы.
Прежде всего, ценная информация:
Основная проблема в заданиях на сумму геометрической прогрессии заключается в правильном определении элементов формулы.
Я не просто так выделяю эти слова. Ибо эти самые элементы составители задач шифруют с безграничной фантазией. Самое главное здесь — не пугаться и не бояться. Что нужно, чтобы не пугаться и не бояться?
1. Разбираться в базовой терминологии. А именно — чётко понимать суть каждого элемента формулы и всей геометрической прогрессии в целом. Об этом можно почитать, посетив первый урок.
2. Знать наизусть формулу n-го члена. Но не просто знать, а уметь грамотно применять на практике. А также уметь работать с её разновидностями — с видоизменёнными и рекуррентными формулами n-го члена. Об этом – во втором уроке.
Начнём с первой задачки на основе варианта ОГЭ.
1. Дана геометрическая прогрессия, знаменатель которой равен -2, а первый член равен -3/4. Найдите сумму первых шести её членов.
Хорошая задачка. Простая. Все исходные данные для применения формулы уже есть. Даны прямым текстом.
Первый член? Пожалуйста!
b1 = -3/4
Знаменатель прогрессии? Вот он!
q = -2
А где взять номер последнего члена? Да всё там же. В условии.) Нас спрашивают про сумму первых шести членов. Стало быть, номер последнего члена — шестёрка:
n = 6
Ещё раз напоминаю, что номер последнего члена всегда совпадает с количеством складываемых членов.
Вот и подставляем все исходные данные в формулу. Подставляем со всеми знаками и скобочками, не стесняемся!)
И аккуратно считаем:
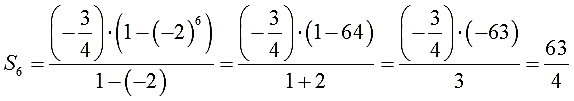
Вот так.
В принципе, ответ уже готов. Если вы просто решаете задачку в классе или дома, то ответ можно так и оставить, в виде обыкновенной дроби. Но если вам нужно записывать ответ в бланк ЕГЭ или ОГЭ то обыкновенную дробь всяко надо перевести в десятичную. Переводим и получаем:
63/4 = 63:4 = 15,75
Ответ: 15,75
Казалось бы, простенькая задачка, но простора для глупых ошибок хватает, да.) Особенно — в знаках. Будьте предельно внимательны при подстановке исходных данных в формулу! Этот пример, с кучей минусов, я специально так подобрал. Иначе задание было бы совсем примитивным…
Ещё один тип популярных задачек:
2. Геометрическая прогрессия задана условием:
b1 = -7,
bn+1 = 3bn
Найдите сумму первых пяти её членов.
Узнали? Да! Та самая рекуррентная формула, от вида которой у многих мурашки по коже… А зря.) Что это за зверь и с чем его едят, подробненько изложено в предыдущем уроке. Кстати, в том уроке детально разобрана задачка именно с нашей формулой, с точно такими же условиями. Совпадение.)
А здесь я буду краток.
Прямо по смыслу рекуррентной формулы считаем второй член прогрессии через первый:
b2 = 3b1 = 3·(-7) = -21
Делим второй член на первый и получаем знаменатель прогрессии:
q = -21/(-7) = 3
Всё! Есть первый член, есть знаменатель. Записываем формулу суммы и считаем сумму пяти членов:
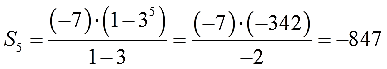
Ответ: -847
А теперь задачка в виде краткой шифровки.
3. Найдите сумму всех натуральных степеней двойки, не превосходящих 1000.
Оп-па! Привычная нам прогрессия блистательно отсутствует: ни первого члена тебе нет, ни последнего… Что делать?
Да всё то же самое! Головой думать, да… Голова нужна не только, чтоб шапку носить.)
Вот и скачиваем из условия задачи всю нужную нам информацию. Что такое натуральные степени — знаем? Правильно! Это степени с целыми и положительными показателями. Т.е. 1, 2, 3 и так далее… И какая такая натуральная степень двойки будет первой? Очевидно, что 21.
Т.е. b1 = 21 = 2.
Можно уже записать прогрессию по условию задачки:
21; 22; 23; 24; 25; …
Будет ли она геометрической? Конечно! Каждый член больше предыдущего строго вдвое. В два раза! Вот уже и знаменатель прогрессии расшифровали незаметно для себя.) Записываем:
q = 2
Осталось лишь сообразить, чему будет равен номер последнего члена n. Из условия задачи видно, что наша прогрессия не простирается вправо на бесконечность. Там чётко сказано: "не превосходящих 1000". Что значит "не превосходящих"? Это значит, меньше или равно — вот! Последний член прогрессии должен быть как можно ближе к тысяче, но не больше её. Меньше — пожалуйста! Ровно тысяча — тоже. А вот больше — уже никак нет.
И как же найти последний такой член?
Очень просто! Берём и последовательно возводим двойку в квадрат, куб, четвёртую степень, пятую и т.д.
И смотрим:
"Так, 28 = 256… мало… 29 = 512, уже ближе, но всё равно маловато… Может, можно ещё возвести? 210 = 1024… Стоп! Уже много! 1024 — уже больше 1000… Стало быть, последний член прогрессии — это два в девятой степени."
Верные мысли! Девятый член нас полностью устраивает. А вот десятый — уже нет: он больше тысячи. Всего на 24, но — больше. Против математики не попрёшь…
Стало быть,
n = 9
Sn = S9
Всё! Вся ценная информация из условия скачана, осталось лишь записать формулу суммы да посчитать:
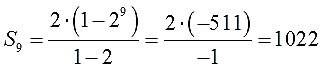
Ответ: 1022
То были простые задачки. Для понимания общей сути и принципа применения формулы. А теперь задачка куда более серьёзная. Подтяните брюки и устраивайтесь поудобнее.)
4. Сумма первых трёх членов геометрической прогрессии равна 26, а сумма следующих трёх членов равна 702. Найдите сумму первых пяти членов.
Что, страшно? Боимся, но решаем!
Перво-наперво, что всегда следует делать в таких задачах — это сразу выписывать общую формулу суммы:
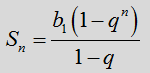
А теперь читаем условие задачи ещё раз и снова начинаем въедливо и настойчиво искать и скачивать любую полезную информацию, любую мелочь, которая может служить зацепкой для применения формулы.
Читаем первое предложение. И сразу же натыкаемся на слова: "Сумма первых трёх членов геометрической прогрессии равна 26…"
Стоп! Это ценно. Можно записать:
S3 = 26
Или, через общую формулу для n=3:
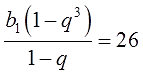
Поможет нам это уравнение или нет — непонятно. Ни первого члена нет, ни знаменателя… Но что-то же делать всё равно надо, верно?) Ничего страшного, условие задачи ещё не окончено.
Читаем дальше: "…а сумма следующих трёх членов равна 702."
Так, это тоже важно! Что такое сумма следующих трёх членов? Это значит, сумма членов с четвёртого по шестой, вот! Ну, раз уж первая сумма была с первого члена по третий…
Пишем:
S4-6 = 702
Хотелось бы это равенство также расписать через общую формулу, но… вынужден вас горько разочаровать.
Напоминаю, что общая формула суммы работает всегда строго с первого члена. А здесь суммирование начинается с четвёртого члена. Облом… Придётся головой думать и как-то выкручиваться, да.)
Самое элегантное решение здесь следующее. Разобьём нашу прогрессию на две части. Первая часть будет с первого члена по третий. Вторая часть — четвёртого члена по шестой. Ясное дело, что если мы возьмём сумму членов первой части S1-3 да сложим её с суммой членов второй части S4-6, то получим… получим… Да! Получим сумму членов с первого по шестой!
Записываем:
S1-3 + S4-6 = S1-6
Обе суммы слева нам известны по условию. Это 26 и 702, если вы помните. Складываем и получаем:
S1-6 = 702+26
S1-6 = 728
Вот и отлично. Теперь сумма считается как и положено — с первого члена. Т.е. к этому равенству уже применима стандартная формула суммы для n=6. Приступаем?)
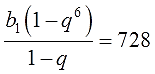
Вот и второе уравнение в кармане!) Так как оба уравнения относятся к одной и той же прогрессии и должны выполняться одновременно, то самое разумное — собрать их в систему. Вот так:
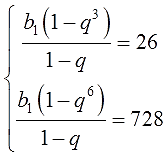
Всё! Работа с собственно прогрессией закончена. Дальше — обычная алгебра. Решение систем — это уже её родная стихия.
Начнём-с?
Хм… не начинается… Ужас какой-то! Дроби, знаменатель q вообще аж в шестой степени. Не простейшая система, ох, не простейшая…
Что ж, пришло время поразмышлять синим цветом:
"Так-с… Влёт не решается, это ясно. Но, тем не менее, какой бы страшной на вид система ни казалась, всегда надо стараться начинать с самого простого и привычного. А именно — прикинуть, а можно ли в каком-то из уравнений выразить одну из переменных через другую? Удобное при этом выражение получится или не очень — дело другое. Главное — выразить! Хоть как-то… Дальше видно будет…"
В данном случае такая возможность есть. Выпишем, например, первое уравнение:
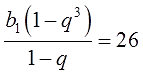
Понятное дело, что пробовать выражать из него q через b1 весьма затруднительно: знаменатель — он сидит под кубом в числителе, да ещё и тусуется в знаменателе. Нехорошо… Зато b1 выступает простым множителем в числителе дроби и больше нигде не сидит! Стало быть, выражать наоборот — b1 через q — одно удовольствие.) Если с блеском владеть тождественными преобразованиями уравнений, и уметь выражать переменную из формулы, конечно…
Вот и "очищаем" b1 от всего постороннего: домножаем всё уравнение на знаменатель 1-q и делим на скобку (1-q3). Всё как при работе с обычным произведением. Получим следующее:
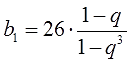
Вот и всё. Слева — только b1, а справа — что уж получилось… Дальше дело привычное. Подставляем это добро в нижнее уравнение. По правилам действий с дробями и дробными выражениями, разумеется:
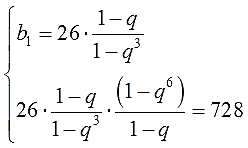
Несмотря на грозный вид нижнего уравнения, оно совсем-совсем простое! Для тех, кто на "ты" с алгеброй седьмого класса, разумеется.) Не верите? Хорошо, убеждаемся лично.)
Выпишем отдельно этого монстра и поработаем:
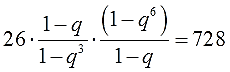
Применяем базовый принцип всей математики:
Не знаешь, что нужно — делай что можно!
Во-первых, можно заметить, что число 728 прекрасно делится на 26! Получится 28. Стало быть, обе части можно сократить на 26. Слева останется произведение дробей, а справа — число 28. Это уже кое-что…)
Поработаем теперь с дробями. А там что можно увидеть? Разность квад… Да! Ну, конечно.) Разложим по формуле разности квадратов самую злую скобку, с шестой степенью:
1-q6 = 12-(q3)2 = (1-q3)(1+q3)
Вот так. Разлагать скобки дальше по формулам разности и суммы кубов никакой необходимости нет. Всё нехорошее и так прекрасно сокращается:
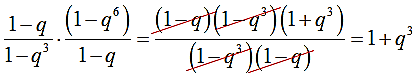
Отлично! Наше злое уравнение превращается в совсем простенькое:
1+q3 = 28
Дорешиваем элементарщину и получаем q=3. Есть! Полдела сделано.)
Имейте в виду, что подобные разложения по формулам сокращённого умножения очень популярны при работе с суммой геометрической прогрессии! Очень! Именно они позволяют максимально эффективно упрощать страшные дробные выражения, превращая их в белые и пушистые.)
Подставляем теперь тройку вместо q в общее выражение для b1 и считаем первый член:
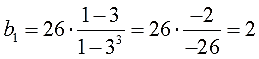
Прекрасно! Первый член есть, знаменатель — тоже. Остался последний штрих — расписать формулу суммы пяти членов, подставить числа да аккуратно посчитать:
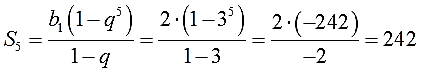
Ответ: 242
Разумеется, разбирать так детально одну задачу смысла особого нету. Не попадётся она. Но самое главное в процессе такого разбора конкретной задачи – показать, как нужно видеть цель и куда именно надо стремиться при решении запутанных примеров. Идея ясна?)
Подытожим урок:
1. При решении любой задачи на сумму геометрической прогрессии первым делом выписываем общую формулу суммы
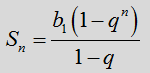
и формулу n-го члена
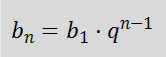
Очень часто совместное применение этих двух формул подсказывает дальнейшую дорогу к ответу.
2. В сложных задачах при работе с формулой суммы применяем разложение на множители по формулам разности квадратов и (или) разности кубов. Основная цель — максимально упростить получающееся уравнение или систему уравнений. Используем эти формулы себе во благо! Помогает.)
Ну что, пора поработать самостоятельно, как вы считаете?)
Решить следующие задачи:
5. Выписаны первые несколько членов геометрической прогрессии:
-256; 128; -64; …
Найдите сумму первых семи её членов.
6. Геометрическая прогрессия задана условием bn = 164∙2-n. Найдите сумму первых четырёх её членов.
Узнали? Всё верно, это формула n-го члена для конкретной прогрессии. Предыдущий урок вам в помощь! Ну и элементарный смысл геометрической прогрессии, разумеется.) Что? Минус в показателе смущает? Ну, это вопрос не к прогрессиям… К степеням, к степеням, товарищи!)
Следующая задачка более творческая. Старинная, между прочим!)
7. Некто продал лошадь за 1000 руб 15 коп. Но покупатель, приобретя лошадь, раздумал ее покупать и возвратил продавцу, говоря:
- Нет мне расчета, покупать за эту цену лошадь, которая таких денег не стоит!
Тогда продавец предложил другие условия:
- Если по-твоему цена лошади высока, то купи только её подковные гвозди, лошадь же получишь тогда в придачу бесплатно. Гвоздей в каждой подкове 6. За первый гвоздь дай мне всего 1 коп., за второй - 2 коп., за третий - 4 коп. и т.д.
Покупатель, соблазненный низкой ценой и желая даром получить лошадь, принял условия продавца, рассчитывая, что за гвозди придется уплатить не более 100 руб.
На сколько рублей покупатель проторговался?
И это решили? Молодца! Хорошо, вот вам ещё парочка задачек покруче.)
8. Второй член возрастающей геометрической прогрессии составляет 4% от четвёртого члена, а сумма первых пяти членов равна 1562. Найдите первый член прогрессии.
9. Сумма второго и шестого членов геометрической прогрессии равна 34, а сумма третьего и седьмого членов равна 68. Найдите сумму первых 10 членов прогрессии.
Ответы (в беспорядке): 2; 166772; 1023; 153,75; -172.
И это решили? Респект! Значит, задачи на сумму геометрической прогрессии — не ваша головная боль. Можно смело двигать на следующий, последний уровень. Под названием бесконечно убывающая геометрическая прогрессия. Специфическая и очень интересная штука, между прочим!)
