Решение показательных уравнений. База для уверенной работы.

Итак, друзья, на прошлом уроке мы с вами познакомились (или научились — кому как) решать самые простые показательные уравнения.

По итогам прошлого урока, в вашей светлой голове должна была остаться общая ключевая информация, касаемо подхода к решению показательных уравнений. Что-то в виде практических советов, а что-то — в самых общих чертах, исходя из примеров, разобранных на уроке.

По пунктам:

1. Первым делом всегда смотрим на основания. Если основания степеней разные, то прикидываем, нельзя ли как-то сделать их одинаковыми. В первую очередь, пытаемся это делать, активно используя действия со степенями и умение распознавать одно и то же число в разных степенях — целых, дробных и отрицательных.

2. Стремимся привести показательное уравнение к каноническому виду, когда слева и справа стоит одно и то же число в каких угодно степенях. Для этого активно используем действия со степенями и базовые тождественные преобразования уравнений (перенос вправо-влево и умножение/деление).

3. Степени популярных чисел надо уметь узнавать в лицо! Пробуем делать это.

4. Действия со степенями надо знать и уметь применять. Причём в обоих направлениях (слева направо и справа налево)!

В приведённых советах, если как следует вчитаться и присмотреться, можно заметить очень частое употребление слов: «пытаемся», «пробуем», «стремимся». Это ключевые слова не только в показательных уравнениях, а во всей математике вообще. Кто пытается, пробует, стремится, у того и получается. Возможно, не сразу, но рано или поздно — обязательно получается! И не только в математике, между прочим. У того же, кто не пробует — не получается ни-че-го! Ничего не поделать. Так уж устроена эта коварная жизнь. К сожалению. Или к счастью.)

Ну что, продолжаем наращивать наш потенциал?

Уровень 3. Раскладываем на множители!

К сожалению, для успешного решения очень многих примеров, одних только примитивных действий со степенями и базовых тождественных преобразований уравнений недостаточно. Необходимо ещё грамотно уметь применять и весь остальной набор ваших знаний и умений из младших и средних классов. Вы же не сразу в старшие классы пошли, не так ли?

Например, разложение на множители. Привет 7-му классу! Это, между прочим, один из самых популярных приёмов в решении очень многих видов уравнений, не только показательных!

Например, вот такое уравнение:

5^x⁺²– 5^x⁺¹ + 5^x = 105

Первый совет (выход на одинаковые основания) здесь не нужен: основания всех степеней уже одинаковые — пятёрка.

Второй совет (приведение к каноническому виду) здесь тоже пока что не работает: из 105 пятёрку в «красивой» степени никак не сделаешь. Убирать пятёрки тоже не имеем права: во-первых, из-за мешающего нам числа 105, а во-вторых, слева нам необходима одинокая степень пятёрки. А у нас там этих пятёрок целая прорва… Причём сделать из этих трёх пятёрок одну также нельзя: нету в математике стандартных правил на сложение и вычитание степеней…

Тупик? Вовсе нет!

Для хоть какого-то продвижения вперёд вспоминаем базовое правило всей математики:

Не знаешь, что нужно — делай, что можно!

Вот и смотрим на наше злое уравнение. Причём не просто пучим глазки, думая о чём-то своём, далёком, а именно внимательно всматриваемся. Что в левой части можно сделать? Да там прямо-таки напрашивается вынесение общего множителя за скобки! Но… где же там общий множитель?! Не видите? Ну ладно. Сейчас покажу!

Начнём с первого слагаемого — с выражения 5^x⁺². По правилам действий со степенями, это выражение мы имеем полное право переписать вот так:

5^x⁺² = 5^x·5²

Почему именно так? А как же! Ну ладно, давайте перемножим обратно. По правилу перемножения степеней с одинаковым основанием:

5^x·5² = 5^x⁺²

Вот и всё, никаких хитростей. Просто здесь, как раз, именно тот самый случай, когда правило действий со степенями

a^m·aⁿ = a^m⁺ⁿ

надо применять справа налево! А я предупреждал: действия со степенями надо уметь применять в обоих направлениях! Да, непривычно, я не спорю. Но ведь и мы тоже серьёзными темами с вами всё-таки занимаемся.) Привыкайте.)

С выражением 5^x⁺¹ полная аналогия:

5^x⁺¹ = 5^x·5¹

Вставляем теперь наши результаты в уравнение:

5^x·5² - 5^x·5¹ + 5^x = 105

Ну как, осеняет? Да! Теперь уже редкий кадр не увидит, что выносить за скобки надо 5^x. Вот и выносим:

5^x(5² - 5¹ + 1) = 105

Что дальше можно сделать? Ну, очевидно, можно посчитать выражение в скобках:

5² - 5¹ + 1 = 25-5+1 = 21

Уравнение из злого постепенно превращается в белое и пушистое:

21·5^x = 105

Вспоминаем теперь, что для ликвидации оснований нам необходима одинокая степень, безо всяких коэффициентов. А число 21 нам мешает. Не беда! Запускаем в ход второе базовое тождественное преобразование и делим обе части на 21. Элементарную математику пока что никто не отменял, да.)

Получаем:

5^x = 5

Вот всё и наладилось! Вот мы и вырулили на одинаковые основания слева и справа!

5^x = 5¹

x = 1

Это окончательный ответ.)

"Многа букафф", да. Но зато понятно, надеюсь. Кстати, кто на «ты» со степенями, тот сразу вынесет 5^x за скобки, не расписывая так подробно. Знания — они иногда помогают. Если они есть, конечно…

Запоминаем: если в уравнении стоит сумма (разность) одного и того же числа в разных степенях, то пробуем применить разложение этой суммы (разности) на множители! А именно — вынесение общего множителя за скобки. Очень часто пример значительно упрощается, и дальнейшая дорога к ответу становится простой и понятной. Всё что можно посчитать в числах — считаем!

В этом примере мы снова вырулили на одинаковые основания путём элементарных преобразований, сведя исходное уравнение к каноническому виду. А именно — с помощью разложения на множители. К сожалению, такой удачный исход при решении показательных уравнений возможен далеко не всегда. Случается, что выруливание на одинаковые основания получается, а вот полная их ликвидация — уже никак. Такое явление происходит в уравнениях другого типа. Освоим и его.

Итак, знакомьтесь!

Уровень 4. Делаем замену переменной!

Для начала решим вот такое уравнение:

9^x - 4·3^x + 3 = 0

Сначала всё как обычно. Основания разные — девятка и тройка. Ничего, тройка в квадрате — это как раз и будет девятка. Так что выправление оснований никаких проблем не вызывает — приводим все степени с иксами к тройке:

9^x = (3^x)² = 3²^x

Получаем вот такое уравнение:

3²^x - 4·3^x + 3 = 0

А вот тут-то и застрянем. Старые советы здесь не помогут: как ни ухищряйся, как ни уединяй степени хоть слева, хоть справа, что ни выноси за скобку, канонический вид уравнения (слева и справа степень тройки) мы всё равно не получим. Кстати, кому интересно, можете попробовать: это полезно.)

Так что же делать? Что-что… Придётся раскрывать вам новое секретное супероружие, предназначенное как раз именно для расправы с такого рода примерами. Да! Это замена переменной!

Суть любой замены всегда проста до безобразия. Вместо одного сложного выражения мы пишем новую букву. Пусть t, например. Или y. Казалось бы, и какой в этом смысл? Ничего, сейчас интересно будет!

В нашем примере прямо таки напрашивается заменить выражение 3^x новой буковкой. Вот и попробуем. А там — видно будет.

Итак, пусть

3^x = t

Тогда, по правилам действий со степенями:

3²^x = 3^x^·2= (3^x)² = t²

Ух ты! Кажется, я уже потихоньку догадываюсь, что получится… Ну-ка, ну-ка… Заменяем в уравнении все выражения с иксами на t:

t² — 4t + 3 = 0

Ну и как вам? Квадратные уравнения ещё помните, я надеюсь?)

Решаем через дискриминант (или по теореме Виета) и получаем два корня:

t₁ = 3

t₂ = 1

А вот теперь, главное, не останавливаться, как это часто бывает. Это пока ещё не ответ: мы же икс с вами ищем! А буковка t — лишь вспомогательное средство.) Стало быть, возвращаемся к иксу, то есть делаем обратную замену.

Начнём с t₁:

t₁ = 3

3^x = 3

x₁ = 1

Отлично. Один корень нашли. Теперь ищем второй, уже из t₂:

t₂ = 1

3^x = 1

О-па! Слева 3^x, а справа 1… Какая-то нестыковочка… Как же нам из единички сделать справа тройку? Как-как… Да снова свойства степеней вспомнить!) А именно: единичка — это любое число в нулевой степени! Да-да! Совершенно любое (кроме нуля).) Какое хотим, такое и сделаем. Нам нужна тройка. Вот и пишем:

1 = 3⁰

3^x = 3⁰

x₂ = 0

Вот и всё. Получили два корня:

x₁ = 1

x₂ = 0

Это окончательный ответ.

Разберём теперь пример посложнее.

2^x⁺² + 7·2^0,5^x — 2 = 0

Здесь тоже старые советы не действуют. Основания одинаковые, но никакими преобразованиями уединению слева и справа не поддаются: что-то обязательно будет мешаться — либо соседи, либо коэффициенты.... Ну что, попробуем замену? Вопрос — что и как заменять будем? А вот тут уже задачка…

Для любой замены чётко уясним себе одну простую вещь: замена переменной оправдана тогда и только тогда, когда в примере в разных местах стоят одинаковые выражения с иксом.

У нас есть выражения 2^x⁺² и 2^0,5^x. Первое выражение, по правилам действий со степенями, можно немного упростить и переписать вот так:

2^x⁺² = 2^x·2² = 4·2^x

Уже лучше. Остались лишь 2^x и 2^0,5^x. Уже почти похоже.) А вот теперь начинаем прикидывать и размышлять. Примерно так:

«Если мы за t примем 2^x, то что нам тогда нужно сделать с 2^x, чтобы получить 2^0,5^x? Очевидно, возвести в степень 0,5. То есть, 2^0,5^x = t^0,5 = t^1/2.

Или, по правилам действий с дробными показателями:

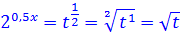
Тогда после такой замены у нас получается иррациональное уравнение с корнями. Как-то оно не очень…

Так, стоп! А что, если попробовать взять за t не 2^x, а наоборот 2^0,5x? Тогда, для того чтобы из 2^0,5^x сделать 2^x, надо 2^0,5^x… возвести в квадрат! Ух ты! Получится квадратное уравнение! Отлично!»

Да! Именно так.) Вот такая нетривиальная замена. Сразу и не увидишь. Работает привычка. Ну и крепкая дружба со степенями, разумеется.

Итак, пусть

2^0,5^x = t

Тогда

2^x⁺² = 2^x·2² = 4·2^x = 4·(2^0,5^x)² = 4t²

Заменяем все конструкции с иксами на выражения с t и получаем:

4t² + 7t — 2 = 0

Так и есть! Снова вышли на квадратное уравнение! Решаем его и получаем корни:

t₁ = -2

t₂ = 0,25

А теперь возвращаемся к иксам, делаем обратную замену.

t₁ = -2

2^0,5^x = -2

Хм… В какую же такую степень надо возвести двойку, чтобы получить минус два? А вы попробуйте, повозводите! Возьмите полный набор самых разнообразных иксов — целое, дробное, отрицательное, нулевое… Минус два вы всё равно никогда не получите. Но! Самые наблюдательные могут заметить, что, во что двойку ни возводи, всё время будет получаться строго положительное число! А вот этот факт уже очень важен!

Итак, запоминаем:

Положительное число в любой степени даёт также положительное число.

Стало быть, нету таких иксов, которые нам минус два дадут. В таких случаях пишут:

t₁ = -2 — посторонний корень

Но это пока ещё не всё: у нас же есть ещё t₂!

t₂ = 0,25

2^0,5^x = 0,25

А вот здесь всё нормально:

2^0,5^x = 25/100 = 1/4 = 2^-2

2^0,5^x = 2^-2

0,5x = -2

x = -4

Вот теперь всё. Получили единственный корень x = -4.

Разумеется, применять замену переменной возможно не только в показательных уравнениях, сводящихся к квадратным. В любых! Лишь бы было что и как заменять. Например, вот такое уравнение:

3^x + 7·3^1-^x = 10

Здесь та же история. Да, основания одинаковы, но сами степени никак не уединяются, выкидывать тройки - нельзя. Разложение на множители тоже не катит: за скобку ничего не выносится, да и десятка всё время мешаться будет… Остаётся замена. Но, ещё раз напоминаю, что замена оправдана только тогда, когда в уравнении в разных местах стоят одинаковые выражения с иксом! Вот и пробуем сначала добраться до одинаковых выражений!

Первым делом упрощаем выражение 3^1-^x по правилам действий со степенями:

3^1-^x = 3¹·3^-x = 3·3^-^x

Тогда наше уравнение станет таким:

3^x + 7·3·3^-^x = 10

Или, если ещё чуток упростить:

3^x + 21·3^-^x = 10

Уже получше. В одном месте в уравнении сидит 3^x, а в другом 3^-^x. Похоже, но всё-таки не одно и то же, да… Снова тупик? Да вовсе нет! Мы с вами знаем, что от минуса в степени математика, если надо, позволяет избавляться! Вот так:

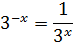
И теперь наше уравнение станет выглядеть вот так:

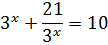
Вот и всё! Теперь, кроме 3^x, никаких других выражений с иксом в нашем примере больше нет. Делаем замену переменной:

3^x = t

Тогда наше уравнение станет вот таким:

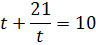
Ну как? Узнали? Да! Это классическое дробно-рациональное уравнение. Куда более привычное, нежели исходное показательное, правда?

А дальше действуем по всем правилам решения дробно-рациональных уравнений: умножаем обе части на t, приводим подобные, собираем всё слева и получаем:

t² — 10t + 21 = 0

Решаем квадратное уравнение и получаем корни:

t₁ = 3

t₂ = 7

А вот сейчас интересно будет! Возвращаемся к нашим иксам.

Начинаем с t₁:

t₁ = 3

3^x = 3

x₁ = 1

Здесь ничего особенного… Хорошо, на очереди следующий клиент t₂:

t₂ = 7

3^x = 7

Опаньки! Из тройки семёрку через простую степень никак не сделаешь! Не родственники они… Как тут быть? Нет ответа?

Спокойствие, как говорил Карлсон! Математика своих в беде никогда не бросает! Она нам на этот случай придумала логарифмы! Посему, если вы в теме, то хладнокровно игнорируем этот жуткий факт и с блеском в глазах записываем твёрдой рукой совершенно верный ответ:

x₂ = log₃7

Вот и всё. Получили тоже два корня:

x₁ = 1

x₂ = log₃7

Естественно, в заданиях на ЕГЭ из части 1, которые проверяет компьютер, такого экзотического ответа быть никак не может: там всегда конкретное число требуется. А вот в заданиях части 2, с развёрнутым решением, которые проверяются экспертами (т.е. людьми) — запросто! Так что будьте готовы и к таким сюрпризам. Чтобы не зависать, в случае чего.)

Подытожим темку:

Замена переменной, порой, существенно упрощает внешний вид примера! В этом и есть весь смысл замены. Очень часто с виду тупиковая ситуация с показательными выражениями после удачной замены превращается в простой и очевидный путь к правильному ответу. Характерные признаки применения замены переменной — присутствие (или получение) одного и того же выражения в разных местах примера.

Уровень 5. Не самые простые примеры. И некоторые дополнительные фишки…

Некоторые примеры не решаются стандартными методами — выравниванием оснований и уединением степеней, вынесением общего множителя за скобки, заменой переменной. Нет, ну не то что бы совсем-совсем не решаются… Это я зря математику обидел.) Но в таких примерах, как правило, дополнительно требуется смекалка и умение нестандартно мыслить. Хотя бы самую малость. Чтобы догадаться до какого-то нетривиального хода, который и спасёт положение.)

Но основная проблема состоит в том, что умение нестандартно мыслить, в большинстве своём, не даётся от природы. Его у себя надо развивать. Даже людям, способным к математике. Как именно его надо развивать?

Что ж, дам несколько самых общих правил.

Правило №1 — Нужно интересоваться математикой!

Да-да! А вы как думали? А иначе какой же смысл браться за сложные (и не только) примеры?

Правило №2 — Нужно чётко понимать основные школьные понятия и термины математики.

Конкретно по нашей теме:

Что такое степень? Как возводить в степень? Какие бывают правила действий со степенями?

Что такое отрицательные и дробные показатели и что с ними можно делать?

Какие вам известны базовые тождественные преобразования уравнений?

Что такое логарифм и зачем он нужен?

Может ли положительное число при возведении в степень дать отрицательное число?

И так далее. Вот берёте, задаёте сами себе определённый вопрос по той или иной теме (в нашем случае — степени и действия с ними) и пытаетесь своими словами, безо всяких заумных фраз, ответить на него. Как именно вы понимаете то или иное понятие, что это такое и как это употребить в дело.

Прошу заметить, что «выучить» и «понимать» - вещи разные. Выучить, скажем, определение логарифма и понять смысл этого самого логарифма — две большие разницы! В первом случае вы зависните на любом нестандартном, хотя и элементарном вопросе на эту тему, а во втором — скорее всего, даже не заметите проблем.

Правило №3 — Нужно знать основные формулы школьного курса математики.

Но одного только знания формул мало. Нужно ещё уметь узнавать формулы, узнавать видоизменённые формулы, уметь применять формулы слева-направо и справа-налево. Это всё очевидно, но… сами понимаете.)

Правило №4 — Нужно не бояться.

А именно — не бояться браться за сложные примеры! Пробовать, пытаться шаг за шагом упростить пример и, возможно, найти решение. Один способ, другой, третий… Что-то подходит, а что-то нет. Это совершенно нормально.

Правило №5 — Нужно думать…

А вот с думаньем дело обстоит хуже всего, да… Нет, думается что-то, конечно. Иногда озаряет даже. Как молния.)

К сожалению, как правильно думать, в книжках и в интернете не написано. Это как-то само собой образуется. С богатым опытом. Но некоторые примеры правильных мыслей и рассуждений я не зря выделяю синим цветом! Обращайте на них внимание!

Итак, обо всём об этом — на этом уровне!

А теперь разбираем примеры. Начнём с довольно безобидного. Решаемого в уме, между прочим.) Если понимать смысл. Допустим, перед нами вот такое уравнение:

2^0,17x + 3^0,3x+1 + 5^0,23x+2 = -5

И что тут можно сделать? Похоже, что… ничего.) Совершенно немыслимый набор степеней. Основания разные, друг в друга через степень не превращаются. Показатели — вообще ахтунг!

Кстати, это и есть подсказка. Значит, где-то спрятан какой-то нестандартный обходной путь, который спасёт положение. И путь этот, скорее всего, до ужаса элементарный…

Что ж, вскрою этот тайный ход. Обращаемся к Правилу №2 и вспоминаем наши самые общие сведения о степенях. А чуть конкретнее — пример, где я предлагал вам повозводить двойку в самые разнообразные степени. Забыли? Зря. Из того примера у вас должно было остаться важное знание. А именно — положительное число в любой степени даёт также положительное число.

Конкретно в нашем примере:

2^0,17x>0

3^0,3x+1>0

5^0,23x+2>0

А теперь осмысливаем: может ли сумма положительных чисел дать нам в результате минус пять? Конечно же, нет! Ни при каком иксе такое равенство не получится.

Ответ: корней нет.

Возможно, кто-то подумает, что этот пример я дал чисто для прикола. Нет! В серьёзных заданиях (скажем, в задачах части 2 из ЕГЭ) необходимо уметь выкидывать целые куски примера из детального рассмотрения. Чтобы не зависать и не тратить время зря на поиск очевидного ответа.

А вот следующий пример уже так просто не спишешь, да…

Решить уравнение:

6^x — 9·2^x - 8·3^x + 72 = 0

Начинаем размышлять:

«Хм… И что тут можно сделать? Основания — разные, к одному и тому же числу никак не сводятся. За скобку ничего не вынесешь. И замена тоже не проходит. Пример явно не простейший…

Но… Вообще говоря, чем больше одинаковых выражений в примере и меньше разных, тем лучше! Поэтому, первым делом, преобразую-ка я выражение 6^x. Разложу шестёрку как 2·3, связав 6^x с уже имеющимися в примере выражениями 2^x и 3^x:

6^x = (2·3)^x = 2^x·3^x»

Вот вам наглядный пример того, как нужно правильно думать. Да! Разложим 6^x на отдельные степени двойки и тройки. Ну ведь явно ни к чему здесь шестёрка! Что получим:

2^x·3^x — 9·2^x - 8·3^x + 72 = 0

Продолжаем размышления:

«И дальше что? В уравнении есть 2^x и есть 3^x. Из двойки тройку через простую степень не сделаешь, это понятно. Стало быть, можно даже не пытаться как-то выровнять основания. Хорошо было бы как-то разделить разные виды показательных выражений. Но как этого можно добиться? Только одним путём - попробовать разложить левую часть на множители! Тем более, что справа в уравнении стоит ноль! Это явный намёк…

За скобку тут ничего не вынесешь, так как общего множителя, сидящего во всех слагаемых, здесь нет. Но! У нас же есть ещё один оч-чень мощный способ разложения подобных выражений! Группировка называется.) А не попробовать ли сгруппировать слагаемые таким образом, чтобы всё получилось? Ну-ка, посмотрим…»

Да! Именно так. Только группировка в этом злом примере даёт нам шанс растащить разные типы показательных выражений (2^x и 3^x). Так что пробуем и группируем. Других вариантов как-то выкрутиться просто нет. Заключаем в скобочки выражения, в которых точно есть общий множитель, есть что вынести.

Хотя бы вот так:

(2^x·3^x — 9·2^x) — (8·3^x — 72) = 0

Теперь видно, что в первых скобках можно вынести 2^x, а во вторых — восьмёрку. Выносим:

2^x(3^x — 9) — 8(3^x — 9) = 0

Вот и отлично. В скобках остались совершенно одинаковые выражения! И теперь эти скобочки сами стали общим множителем. Можно и их вынести:

(3^x — 9)(2^x — 8) = 0

Всё! Слева — произведение скобок, справа — ноль. А дальше уже всё ясно: произведение равно нулю тогда, когда хотя бы один из множителей равен нулю.

Обратите внимание, как красиво разделились разные типы показательных выражений! Разошлись по своим скобочкам. И теперь каждую из них стало возможно рассматривать независимо друг от друга!

Приравниваем к нулю первую скобочку:

3^x — 9 = 0

3^x = 9

3^x = 3²

x₁ = 2

Со второй аналогично:

2^x — 8 = 0

2^x = 8

2^x = 2³

x₂ = 3

Вот всё и получилось. Два корня.

Запоминаем: при решении сложных примеров очень часто применяется разложение на множители способом группировки. Основная цель — разделить разные типы показательных выражений.

А вот в следующих двух примерах уже и группировка не спасёт…

Для начала вот такой:

5·3^x - 7·2^x = 0

Казалось бы, коротенькое и простенькое уравнение. Но… За что зацепиться? Совершенно безумный набор чисел, ни одно из них друг в друга не превращается. Специально, поди.) Ни разложение на множители не катит, ни замена…

Спокойствие! На подобного рода примеры тоже есть своё секретное оружие. Называется — почленное деление на показательное выражение. Характерный признак применения такой процедуры — разные основания, но одинаковые показатели. Ибо по нашим незабвенным свойствам степеней мы знаем, что

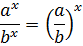
А теперь смотрим на уравнение. У нас есть тройка в степени икс и двойка также в степени икс. И, глядя на уравнение, прямо-таки напрашивается вместо двух разных степеней сделать одну. А что, если поделить обе части уравнения на какое-то из показательных выражений? Например, на 2^x?

Что ж, посмотрим. Делим:

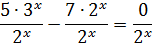
Вот и первый хитрый вопрос: почему я так смело делю всё уравнение на 2^x? Ведь в теме про уравнения открытым текстом сказано, что делить мы имеем право только на отличное от нуля число! А тут в показателе икс есть! Кто ж его знает, какое он там число даст… Подумайте пока, ответ будет чуть ниже, после расправы над этим злым уравнением.

А мы продолжаем. Вспоминаем действия со степенями, сокращаем что сокращается и получаем:

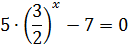
Цель деления достигнута: вместо двух различных значков 3^x и 2^x стал один значок (3/2)^x. Уже гораздо проще, правда?)

А дальше дело техники. Уединяем степень слева: переносим семёрку вправо и делим на пятёрку. Получаем:

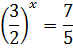
Можно, для краткости, (но не обязательно) перевести дроби в десятичные:

1,5^x = 1,4

Всё. Получено простейшее показательное уравнение. Слева — чистая степень, а справа — число. Правда, сами числа какие-то корявые… Выравнивание не катит… Ну и ладно, ничего страшного. Логарифмы — они выручают всегда!

Так прямо и пишем:

x = log_1,51,4

Вот и всё. Да, такой вот хитрый ответ у примера, через логарифм! Так и уравнение у нас тоже не подарок, прямо скажем. Мы ведь уже на пятом уровне с вами, не так ли? И, кстати сказать, даже по внешнему виду уравнения сразу было понятно, что ответ красивым целым числом не получится.

Возможно, кто-то спросит: «А что, если поделить это же уравнение не на 2^x, а на 3^x? Это как-то повлияет на ответ?» А вы не поленитесь и попробуйте! И сравните. Будет интересно.)

А теперь обещанный ответ на хитрый вопрос, почему же мы можем смело делить всё уравнение на показательное выражение с иксом типа 2^x, 3²^x и т.п. Ведь, казалось бы, в показателе сидит икс! А делить на выражение с иксом мы имеем право лишь тогда это выражение отлично от нуля! А откуда мы знаем, какое там число получится — ноль, не ноль…

Любое число может получиться! Почти… Но не ноль! Ещё раз (уже третий по счёту!) напоминаю, что положительное число в любой степени (в том числе и с иксом!) даёт число положительное! Никогда не получится ни отрицательное число, ни ноль! Именно поэтому такое деление в показательных уравнениях применяется весьма и весьма часто. И, как видите, порой только оно и спасает.

Ну и на десерт рассмотрим ещё одно уравнение на деление. С одной стороны оно посложнее (ибо решается дольше), а с другой - попроще (ибо безо всяких логарифмов, все числа — красивые).

Вот оно:

5·3²^x + 3·5²^x = 8·15^x

С чего начинать? Ну, пока сделаем очевидное преобразование — распишем 15^x как произведение 3^x·5^x. Всё-таки два основания в примере получше, чем три, правда?

Получим:

5·3²^x + 3·5²^x = 8·3^x·5^x

Ну вот, уже гораздо приятнее. В основаниях остались только тройки и пятёрки. Но… Что же дальше? Основания разные, к одному через степень не приводятся. Замена не годится: нету пока что одинаковых выражений с иксами. Вынесение общего множителя за скобки и группировка — тоже не канают: ни выносить нечего, ни группировать… Так, стоп! А что, если поделить обе части уравнения на… да хоть на что-нибудь! Например, на 5²^x.

Что получим:

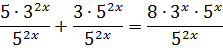
И чем же нам помогло такое, казалось бы, бессмысленное действие? Терпение! Сейчас всё будет! Работаем дальше. Упрощаем каждое слагаемое по правилам действий со степенями, сокращаем то, что сокращается и получаем:

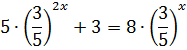
Ну и как? Осенило? Да! Теперь уже очевидно, что можно сделать замену (3/5)^x = t. Получится квадратное уравнение. Кажется, жизнь налаживается!

5t² + 3 = 8t

5t² — 8t + 3 = 0

Решаем и получаем корни:

t₁ = 1

t₂ = 3/5

Возвращаемся к иксам. Для t₁ = 1 получим:

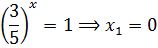
Для t₂ = 3/5 получим:

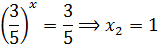
Видите! Всего одно бесполезное, казалось бы, действие (деление на 5²^x) — а эффект колоссальный! Сразу же всё высвечивается — что преобразовать, что сократить, что заменить…

Запоминаем: при решении сложных примеров очень часто применяется почленное деление на показательное выражение. Основная цель — сделать как можно больше одинаковых выражений в примере.

А теперь второй хитрый вопрос.) Мы с вами решаем самые разные показательные уравнения. Простые и не очень. Почему я ни разу не сказал здесь про ОДЗ? В уравнениях это весьма и весьма важная штука, между прочим!

Да, важная, безусловно. Но фишка в том, что показательные выражения типа 2^x, 3²^x и тому подобные, имеют смысл при любом икс! Нету никаких ограничений на показатель степени. Любым может быть показатель. Вот обычно и не вспоминают про ОДЗ в показательных уравнениях.

Но я всё-таки вспомнил. И не зря. Привыкают люди к типовым примерам (когда в показателях стоят простые выражения типа x, 2x+1 и т.п.), вот и не вспоминают про ОДЗ в показательных уравнениях. Вообще! Даже и в таких показательных уравнениях не вспоминают:

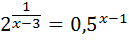
А вот здесь уже есть ограничение! В показателе слева икс не может равняться тройке! На ноль делить нельзя. В том числе и в показателе, да.) И, если по привычке проигнорировать это ограничение, то, чего доброго, можно и ответ неверный получить.

Так что привычка привычкой, но внимание — превыше всего.

Ну что! Поздравляю! Мы с вами успешно поработали с показательными уравнениями на всех уровнях! И теперь — финальный аккорд. Обещанная домашка. Да-да, решать так решать! Вам же экзамен сдавать, а не мне.) Так что меняем мышку на ручку и - тренируемся.)

Уравнения даю вразброс, никак не сортируя их ни по типам, ни по способам решения. Ибо так интереснее.)

Рецепт здесь один: внимательно осматриваем уравнение и сами лично выбираем способ решения. Если сразу не осеняет, то поочерёдно пробуем все известные вам приёмы, о которых я рассказал на прошедших уроках. Что-то сработает, что-то — нет. Это не страшно. Пробуем дальше. Что-то обязательно сработает!

Решить уравнения:

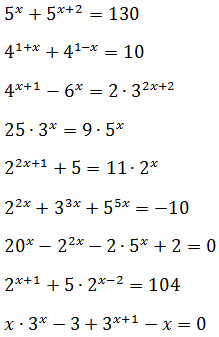
Да-да, прошу не удивляться последнему уравнению! Это уравнение смешанного типа: иксы стоят и в показателях, и просто так. Такие уравнения мы с вами не рассматривали, да.) Но материала этого урока вполне достаточно для успешной расправы с этим монстром. И да поможет вам седьмой класс (это подсказка)!

Ответы (в беспорядке):

x = -2

x₁ = -1 x₂ = log₂5

x = 2

x = 5

x₁ = 0 x₂ = 0,5

x = 1

x₁ = -0,5 x₂ = 0,5

x₁ = -3 x₂ = 0

решений нет