Итак, друзья, я вас поздравляю! Начальный этап знакомства с тригонометрией благополучно пройден. Подытожим его. Теперь мы с вами:
1. Знаем, что такое синус, косинус, тангенс и котангенс в прямоугольном треугольнике.
2. Знаем, как устроена связь между тригонометрическими функциями одного и того же угла и умеем находить полный набор функций, если известна хотя бы одна из них. Кроме того, ещё мы умеем (надеюсь) пользоваться основными тригонометрическими формулами. А чего? Зря, что ли, примеры разбирали?)
Это — самые азы тригонометрии. Без этих элементарных знаний и навыков — дальше никуда. Так что, прошу прогуляться и почитать, пока не поздно. Тем более там всё очень просто и доступно.)
Идём дальше.
Как мы уже с вами знаем, у каждого острого угла в прямоугольном треугольнике имеется свой джентльменский набор тригонометрических функций. Знаем длины катетов и гипотенузу, делим друг на друга и считаем себе. И так для любого острого угла. Всё элементарно.
Вопрос: а если угол сделать тупым? Скажем, вот таким:

Что делать? Развалился наш прямоугольный треугольник. Ни катетов больше нет, ни гипотенузы… А тригонометрические функции тоже ушли в небытие, да?
Если бы древние математики не нашли выход из этой ситуации, то, возможно, вы бы сейчас и не читали этот сайт. Ибо не было бы у нас тогда ни планшетов, ни компьютеров, ни смартфонов, ни многих других полезных штучек…
Так как можно определять любые тригонометрические функции любых углов без прямоугольного треугольника? Что ж, пришла пора взрослеть дальше. Знакомимся!
Тригонометрическая окружность. Единичная окружность. Числовая окружность. Что всё это значит?
Это очень простые понятия. Более того, эти понятия — верный друг и надёжный помощник во всех разделах тригонометрии! От простой работы с углами в градусах или в радианах до тригонометрических уравнений и неравенств. Почему? А потому, что эта штука — своего рода шпаргалка! Причём совершенно законная! Обычно ведь что бывает: за шпоры выгоняют, двойки ставят… А тут нарисовал окружность, угол, функцию — и сразу увидел всё что тебя интересует.
Например, такое простое задание:
Что больше — sin200° или sin(-100°)?
Кто не в теме, тот отдыхает в сторонке. А кто в теме, тот нацарапает что-то типа вот такого наскального рисунка:

и сразу же увидит всю необходимую информацию!
И никто слова не скажет! Даже суровая комиссия в боевой обстановке ЕГЭ. Так зачем же такой шанс упускать, правда?
Чуть позже, в соответствующем уроке, мы разберём эту страшную задачку. И про злые углы типа -100 градусов тоже поговорим.)
А пока начнём. Для начала нарисуем самый обычный привычный нам острый угол. Назовём его, как обычно, "альфа". Вот так:
Угол как угол, пока ничего выдающегося, но… Раз есть угол (пока что острый), то у него должны быть и свои тригонометрические функции! Косинус там или тангенс… А где их взять? Ни гипотенузы, ни катетов больше нет, только угол. Тупик?
Спокойствие! Сейчас всё увидите.)
Для начала нарисуем самые обычные и знакомые нам координатные оси. OX по горизонтали, OY — по вертикали, всё чин-чинарём… Нарисуем и… приколотим горизонтальную сторону угла к положительной полуоси OX. Приколотим покрепче, дабы не оторвать ненароком.) Вершину угла поместим в начало координат, точку О. А вот вторую сторону угла прибивать не будем и оставим подвижной. Зачем? А чтобы угол менять можно было. Хотим побольше, хотим поменьше. Хотим острый, хотим тупой — любой! Раздвижной у нас угол будет. Как угол раствора циркуля, только одна из его ножек будет прибитой.) Конец подвижной стороны обозначим буквой А.
Получим вот такой незамысловатый рисунок:
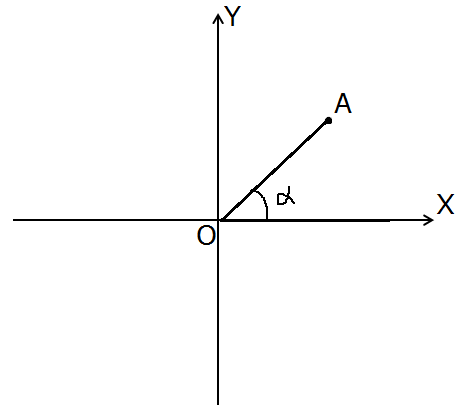
Итак, угол у нас пристроен, это хорошо. А где же его синус и косинус — спросите вы? Потерпите минутку, торопыги, сейчас всё увидите! Я же только начал.)
Введём теперь координаты x и y конца подвижной стороны угла (точки А) и отметим их на осях. Это будут точки В и С соответственно. Ясное дело, что ОВ и ОС — какие-то числа. Длины отрезков. Или координаты точки А.
ОВ = х
ОС = у
Так вот, оказывается, иксовая координата точки А (отрезок ОВ) будет косинусом угла альфа, а игрековая координата (отрезок ОС) — его синусом!
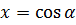
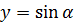
Смотрим на рисунок:
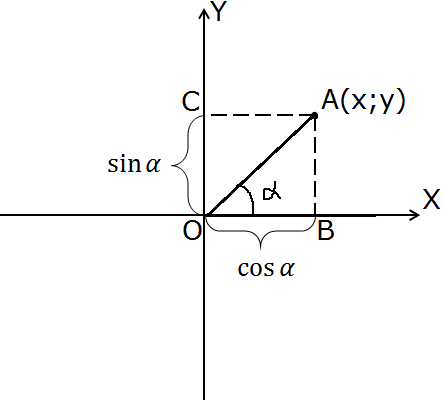
Стоп-стоп! С какого такого перепугу-то? Ведь мы же чётко зарубили себе на носу из прошлых двух уроков, что синус и косинус — это отношения сторон в прямоугольном треугольнике! Которые от длин этих самых сторон никак не зависят. А у нас тут координаты точки А присутствуют. Которые могут быть любыми!
Всё верно. Любыми. Но! Давайте посмотрим внимательнее на треугольник АВО. Прямоугольный, между прочим.) Ибо координаты точки, они обычно перпендикулярами отмечаются на осях, да… По нашему заклинанию косинус угла альфа — это отношение прилежащего катета к гипотенузе. Или ОВ/ОА. Синус альфа — соответственно ОС/ОА. Причём мы с вами помним, что синус/косинус никак не зависят от длин сторон. А это совсем прекрасно! Почему? А потому, что мы имеем полное право выбирать длины сторон как хотим. Как нам удобно, так и выберем. В частности, мы имеем полное право принять длину гипотенузы ОА за единичку (ОА=1)! Причём единицы измерения нас вообще не волнуют — миллиметр, километр, миля, дюйм… Синус и косинус от этого всё равно не изменятся.)
Почему именно гипотенуза (а не катеты) и именно единичка (а не 2, 10, 157 и т.д)? Потому, что так нам (и древним людям) очень удобно! Именно при таком выборе у нас достигаются максимальные упрощения. Смотрите, что получается:
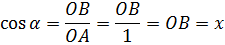
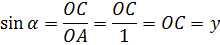
Вот и все дела.) Косинус — иксовая координата точки А, а синус — игрековая (если гипотенуза ОА — единичка). Да, ненаучно, да нестрого, но зато понятно. И запоминается проще. А запомнить очень важно. Причём, запомнить надёжно!
Запоминаем:
Косинус — по Х, синус — по Y.
Именно в таком порядке. Не путаемся!
Как видите, всё просто. Пока что всё идёт в рамках геометрии восьмого класса. С той лишь разницей, что катеты превратились у нас в координаты х и у точки А, а гипотенуза — та и вовсе превратилась в единичку. Очень удобное число.) Однако… Тема урока называется "Тригонометрическая окружность", не так ли? Пока ни слова про окружность не было!
Всё правильно. Но остались совсем пустяки. Сейчас мы с вами резко повзрослеем и колоссально расширим наши возможности всего одним движением руки! Как? Очень просто. Берём подвижную сторону угла (т.е. ОА) и… проворачиваем её вокруг точки О на полный оборот! Как вы думаете, какую линию при этом опишет точка А? Ну, конечно! Окружность!
Вот так:
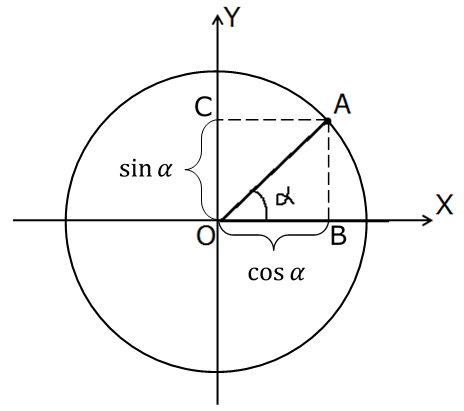
Вот и всё. Это и есть тригонометрическая окружность!
Это научное название. А на математическом сленге обычно говорят "тригонометрический круг". Или совсем коротко — просто "круг". Или — "радар" :).
Ну хорошо, окружность начертили. Но почему — тригонометрическая? Окружность как окружность… Вскрою тайну. Любой точке на окружности соответствуют два числа — координаты этой точки по X и координаты этой точки по Y. То есть, А(х; у). А икс и игрек у нас что? Только что разбирались… Да! Косинус и синус угла альфа. То есть, не что иное, как его тригонометрические функции. Вот и весь смысл.
А теперь, вспомнив, что ОА = 1 и что ОА — радиус окружности, можно сообразить, что это же самое понятие — и единичная окружность тоже.
А если вспомнить самый первый урок по тригонометрии (а чуть конкретнее — то, что синус и косинус — просто какие-то числа), то наша с вами тригонометрическая окружность будет ещё и числовой окружностью.
Вот так. Сразу три термина в одном. Очень удобно и практично.
Запоминаем:
Тригонометрическая, единичная и числовая окружности — это всё одно и то же понятие. В рамках тригонометрии.
Так, ну хорошо. Окружность изобразили. Угол у нас крутящийся, меняющийся. А раз крутящийся, то нам уже ничто не запрещает прокрутить подвижную сторону ОА куда угодно. Например, так, чтобы угол альфа стал каким-нибудь тупым!
Хотя бы вот так:
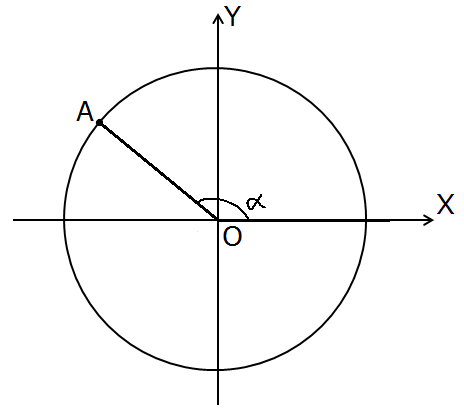
А как увидеть его синус и косинус? Не вопрос! Всё точно так же. Опускаем перпендикуляры из точки А на оси OX и OY и всё видим:
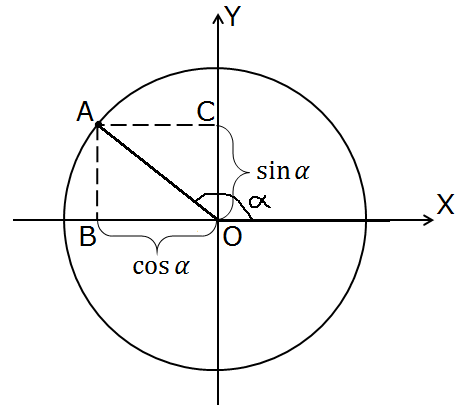
Самые глазастые, возможно, уже заметили, что синус угла альфа у нас положительный (точка С лежит на положительной полуоси OY). А вот косинус альфа — отрицательный! Ибо точка В, иксовая координата точки А (т.е. не что иное, как косинус альфа!), лежит на отрицательной полуоси OХ. Значит, у любого тупого угла синус положительный, а косинус — отрицательный. Чего, кстати, принципиально не бывает в прямоугольном треугольнике: там все тригонометрические функции — синус, косинус, тангенс, котангенс — положительные.
А здесь — пожалуйста! Не зря же мы с вами расширили наши возможности!) Ну а коли так, раз уж мы столкнулись с отрицательным косинусом у тупого угла, то пришла пора разобраться и с такой важной штукой, как знаки синуса/косинуса по четвертям. До кучи и знаки тангенса/котангенса разберём сразу же.
Знаки синуса и косинуса, тангенса и котангенса по четвертям.
Всё проще простого. Для начала напомню, что координатные четверти (или по-другому квадранты) в тригонометрии нумеруются точно так же, как и при работе с обычными задачами на координаты точек — против часовой стрелки.
Вот так:
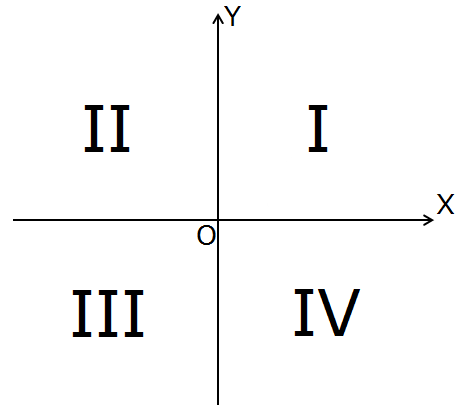
А что же со знаками синуса/косинуса по четвертям? Тоже всё элементарно, Ватсон.) С первой и второй четвертями мы уже разобрались выше. Незаметно для себя.) С первой четвертью вообще вопросов нет. Там только острые углы, у которых все функции (в том числе и синус с косинусом) — положительные. Со второй четвертью тоже всё ясно: синус положительный, а косинус — отрицательный. Это мы уже выяснили, когда тупой угол рисовали.
Осталось лишь разобраться с третьей и четвёртой четвертями. Как? Точно так же! Не зря же мы с вами тут углы мотать учимся потихоньку.)
Мы же знаем, что ОА — подвижная сторона нашего угла альфа. Вот и продолжим её крутить от положительной полуоси ОХ в нужную нам сторону! В третью четверть. Получим вот такую картинку:
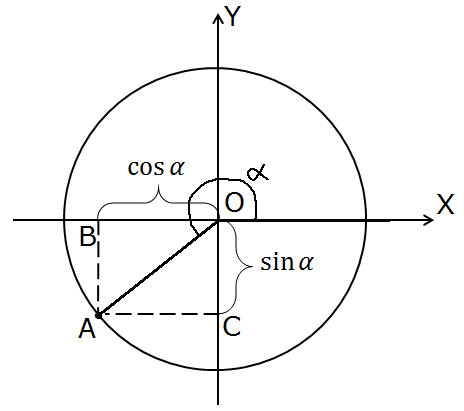
Как видно из рисунка, для любого угла в третьей четверти уже станет отрицательным не только косинус, но и синус тоже:
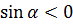
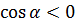
Для четвёртой четверти тоже ничего хитрого. Крутим и рисуем:
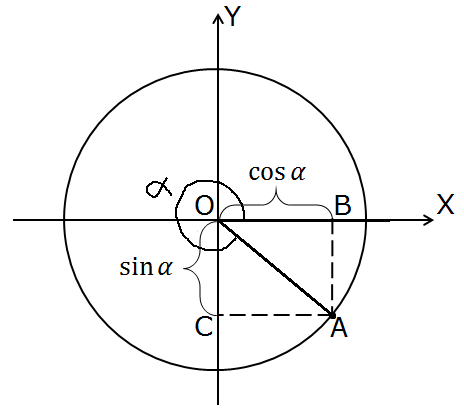
И видим, что синус в четвёртой четверти остаётся по-прежнему отрицательным. А косинус? Да! Косинус снова становится положительным:
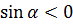
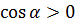
Так, по всем четвертям пробежались. Как видите, всё просто. Для лучшего запоминания можно нарисовать знаки синуса/косинуса прямо на нашем круге.
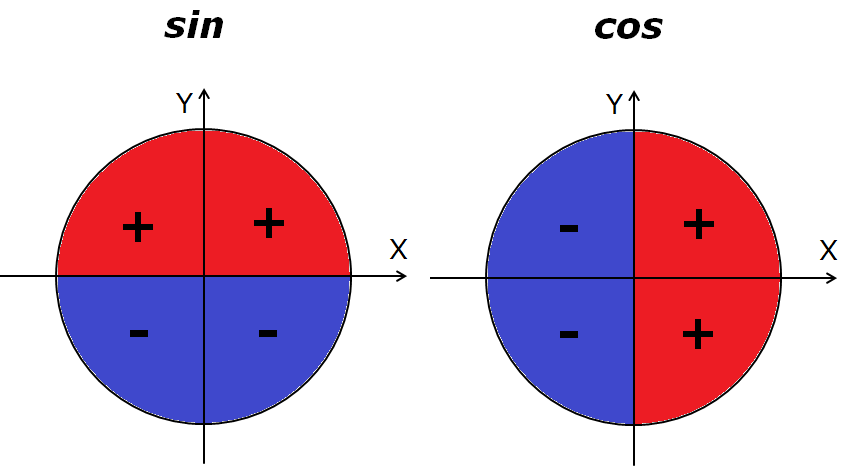
Запоминаются обе картинки достаточно просто и быстро. Особенно если железно помнить наше секретное заклинание: "Косинус — по икс, синус — по игрек." Кстати, сопоставьте заклинание с картинками! Очень полезно.)
Ну хорошо, с синусом/косинусом всё понятно. А тангенс и котангенс? Тоже никаких проблем. Если, конечно, помнить из второго урока, что тангенс — это синус поделить на косинус:
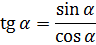
А котангенс — наоборот.
Вот теперь и прикинем. В первой четверти у нас всё шоколадно. Всё с плюсом — и синус и косинус. А плюс поделить на плюс — что будет? Конечно же, плюс! Во второй четверти знаки синуса и косинуса — разные. Плюс и минус. А это значит, что их отношение (что синуса к косинусу, что наоборот) будет всегда отрицательным. Ибо в борьбе минуса с плюсом всегда выигрывает минус. Так уж повелось в математике.) В третьей четверти как синус, так и косинус имеют знак "минус". А их отношение? Минус на минус — будет… будет… плюс! А в четвёртой четверти знаки синуса/косинуса опять разные. Стало быть, их отношение (тангенс с котангенсом) снова будет с минусом! Вот и все дела.)
Получаем для тангенса/котангенса вот такую картинку:
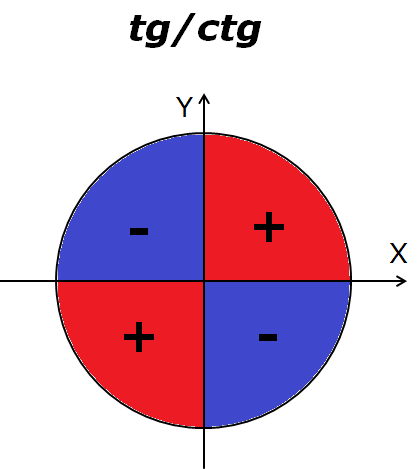
Запомнить знаки тоже проще простого: плюс-минус-плюс-минус. Простое чередование знаков.)
И вот тут у некоторых назревает закономерный вопрос:
А можно ли увидеть тангенс и котангенс на круге? Синус — по игрек, косинус — по икс. Это понятно.) А тангенс и котангенс???
Ух, какие вы любопытные, оказывается! Все-то секреты вам раскрой сразу же! Да, можно! Можно увидеть тангенс и котангенс на числовой окружности! Любого угла. Только для этого на нашем рисунке необходим ещё один дополнительный взмах пера. Всего один. Какой именно — в спецтеме "Тангенс и котангенс на тригонометрической окружности".
Итак, полдела сделали. Нарисовали угол, с его помощью начертили окружность. Осталась вторая половина дела. А именно — научиться проделывать обратную операцию. По любой произвольной точке на окружности научиться определять сам угол! А вот эта задачка та ещё…
Об этом — в следующей теме: "Как отсчитывать углы на тригонометрической окружности?".
