Логарифмы — традиционная головная боль для многих учеников старших классов. Особенно — уравнения и неравенства с логарифмами. Не любят старшеклассники логарифмы почему-то. И поэтому боятся. И совершенно зря.) Ибо сам по себе логарифм — это очень и очень простое понятие. Не верите? Убедитесь сами! В сегодняшнем уроке.
Итак, поехали знакомиться.)
Для начала решим в уме вот такое очень простенькое уравнение:
2х = 4
Это простейшее показательное уравнение. Оно так называется из-за того, что неизвестное икс находится в показателе степени. Даже если вы не в курсе, как решаются показательные уравнения, просто в уме подберите икс так, чтобы равенство выполнилось. Ну же?! Ну, конечно же, х = 2. Два в квадрате — это четыре.)
А теперь я изменю в нём всего одно число. Вот такое уравнение теперь решим:
2х = 5
И снова пробуем подобрать икс…
Что, никак не подбирается? Два в квадрате — это четыре. Два в кубе — это уже восемь. А у нас — пятёрка. Мимо проскочили… Что делать? Только не говорите мне, что нету такого икса! Не поверю.)
Согласитесь, что это как-то несправедливо: с четвёркой уравнение решается в уме, а с пятёркой — уже не решается никак. Математика не приемлет такой дискриминации! Для неё все числа — равноправные партнёры.)
На данном этапе мы можем лишь грубо прикинуть, что икс — какое-то дробное число между двойкой (22 = 4) и тройкой (23 = 8). Можем даже немного повозиться с калькулятором и приближённо подобрать, найти это число. Но такая возня каждый раз… Согласен, как-то грустно…
Математика решает данную проблему очень просто и элегантно — введением понятия логарифма.
Итак, что же такое логарифм? Вернёмся к нашему загадочному уравнению:
2х = 5
Осмысливаем задачу: нам надо найти некое число х, в которое надо возвести 2, чтобы получить 5. Понятна эта фраза? Если нет, перечитайте ещё раз. И ещё… Пока не осознаете. Ибо это очень важно!
Вот и назовём это загадочное число х логарифмом пятёрки по основанию два! В математической форме эти слова выглядят так:
x = log25
А произносится эта запись вот так: "Икс равен логарифму пяти по основанию два."
Число внизу (двойка) называется основанием логарифма. Пишется снизу так же, как и в показательном выражении 2х. Запомнить очень легко.)
Ну, вот, собственно, и всё! Мы решили ужасное на вид показательное уравнение!
2х = 5
x = log25
И всё! Это правильный и совершенно полноценный ответ!
Может быть, вас смущает, что вместо конкретного числа я пишу какие-то непонятные буковки и значки?
Ну что ж, ладно, уговорили… Специально для вас:
x = log25 = 2,321928095…
Имейте в виду, что число это никогда не кончается. Да-да! Иррациональное оно…
Вот вам и ответ на вопрос, для чего нужны логарифмы. Логарифмы нам нужны, в первую очередь, для решения показательных уравнений! Таких, которые без логарифмов и не решаются вовсе…
Например, решая показательное уравнение
3x = 9,
про логарифмы можно не вспоминать. Сразу ясно, что х = 2.
А вот, решая уравнение, скажем, такое
3х = 7,
вы приближённо получите вот такой лохматый ответ:
х ≈ 1,77124375
Зато через логарифм даётся абсолютно точный ответ:
х = log37.
И все дела.) Вот поэтому и пишут логарифмы вместо некрасивых иррациональных чисел. Кому нужен числовой ответ — посчитает на калькуляторе или хотя бы в Excel.) А раньше, когда калькуляторов и компьютеров не было и в помине, существовали специальные таблицы логарифмов. Объёмные и увесистые. Так же, как и таблицы Брадиса для синусов и косинусов. И даже инструмент такой был — логарифмическая линейка. Которая позволяла с хорошей точностью вычислять массу полезных вещей. И не только логарифмы.)
Ну вот. Теперь, незаметно для себя, мы научились решать все показательные уравнения такого зверского типа.
Например:
2х = 13
Никаких проблем:
x = log213
5х = 26
Тоже элементарно!
x = log526
11x = 0,123
И тут не вопрос:
x = log110,123
Это всё верные ответы! Ну как? Заманчиво, правда?
А теперь вдумаемся в смысл самой операции нахождения логарифма.
Как мы знаем, на каждое действие математики стараются найти противодействие (т.е. обратное действие). Для сложения это вычитание, для умножения это деление. А какое обратное действие есть для возведения в степень?
Давайте посмотрим. Какие у нас основные действующие фигуры при возведении в степень? Вот они:
an = b
a - основание,
n - показатель,
b - собственно сама степень.
А теперь подумаем: если нам известна степень (b) и известен показатель этой самой степени (n), а найти надо основание (a), то что мы обычно делаем? Правильно! Извлекаем корень n-й степени! Вот так:
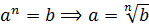
А теперь посмотрим на другую ситуацию: нам снова известна степень (b), но на этот раз вместо показателя n нам известно основание (a), а найти как раз надо этот самый показатель (n). Что делать будем?
Вот тут-то на помощь и приходят логарифмы! Прямо так и пишут:
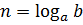
"Эн" (n) — это число, в которое надо возвести "a", чтобы получить "b". Вот и всё. Вот и весь смысл логарифма. Операция нахождения логарифма — это всего лишь поиск показателя степени по известным степени и основанию.
Таким образом, для возведения в степень в математике существует два разных по природе обратных действия. Это извлечение корня и нахождение логарифма. А вот, скажем для умножения обратное действие только одно — деление. Оно и понятно: любой из неизвестных множителей — что первый, что второй — ищется с помощью одной операции - деления.)
Простейшие примеры с логарифмами.
А теперь новость не очень хорошая. Если логарифм считается ровно, то его надо считать, да.
Скажем, если где-то в уравнении вы получили
x = log39,
то такой ответ никто не оценит. Надо логарифм посчитать и записать:
х = 2
А как мы поняли, что log39=2? Переводим равенство с математического языка на русский: логарифм девяти по основанию три — это число, в которое надо возвести три, чтобы получить девять. И в какое же число надо возвести тройку, чтобы получить девятку? Ну, конечно! В квадрат надо возвести. То есть, в двойку.)
А чему равен, скажем, log5125? А в какой степени пятёрка даёт нам 125? В третьей, разумеется (т.е. в кубе)!
Стало быть, log5125 = 3.
Идём дальше.
log77 = ?
В какую степень надо возвести 7, чтобы получить 7? В первую!
Вот вам и ответ: log77 = 1
А вот такой пример как вам?
log31 = ?
И в какую же степень надо возвести тройку, чтобы получить единицу? Неужели не догадались? А вы вспомните свойства степеней.) Да! В нулевую! Вот и пишем:
log31 = 0
Уловили принцип? Тогда тренируемся:
log216 = …
log464 = …
log1313 = …
log3243 = …
log151 = …
Ответы (в беспорядке): 1; 3; 5; 0; 4.
Что? Забыли, в какой степени 3 даёт 243? Что ж, ничего не поделаешь: степени популярных чисел надо узнавать. В лицо! Ну, и таблица умножения — надёжный спутник и помощник. И не только в логарифмах.)
Ну вот, совсем простенькие примеры порешали, а теперь шагаем на ступеньку выше. Вспоминаем отрицательные и дробные показатели.)
Решаем вот такой пример:
log40,25 = ?
Мда… И в какую же степень надо возвести четвёрку, чтобы получить 0,25? Так с ходу и не скажешь. Если работать только с натуральными показателями. Но степени в математике, как известно, бывают не только натуральными. Самое время подключить наши знания об отрицательных показателях и вспомнить, что
0,25 = 1/4 = 4-1
Стало быть, можно смело записать:
log40,25 = log44-1 = -1.
И всё.)
Ещё пример:
log42 = ?
В какую такую степень надо возвести четвёрку, чтобы получить двойку? Для ответа на этот вопрос придётся подключать наши знания о корнях. И вспомнить, что двойка — это корень квадратный из четырёх:
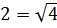
А корень квадратный математика позволяет представить в виде степени! С показателем 1/2. Так и пишем:
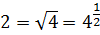
Поэтому наш логарифм будет равен:
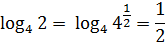
Ну что, поздравляю! Вот мы с вами и познакомились с логарифмами. На самом примитивном начальном уровне.) И вы сами лично убедились, что они вовсе не так страшны, как, возможно, вам казалось раньше. Но у логарифмов, как и у любых других математических понятий, есть свои свойства и свои особые фишки. О том и о другом (о свойствах и о фишках) — в следующем уроке.
А теперь решаем самостоятельно.
Вычислить:
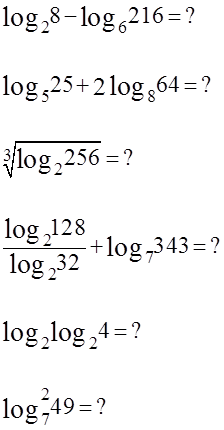
Ответы (в беспорядке): 4,4; 0; 1; 6; 4; 2.
