Логарифмические уравнения — штука, вообще говоря, не самая простая. Слишком уж много их. Простых, суперсложных, всяких.) Кроме того, для их безошибочного решения необходимы пристальное внимание и приличный запас знаний по другим, смежным темам.
А именно:
1. Логарифмы
- Что такое логарифм и что с ним можно делать?
- Ограничения в логарифмах. Свойства логарифмов.
2. Степени
- Базовые действия со степенями.
- Работа с отрицательными и дробными показателями.
3. Уравнения
- Тождественные преобразования уравнений.
- Что такое ОДЗ и куда её пристраивать?
4. Алгебра и её общие правила и законы
А именно: приведение подобных, разложение на множители, формулы сокращённого умножения и т.д.
Именно эти четыре ножки позволяют сидеть твёрдо, надёжно и не падать на ровном месте. Ибо больно это.) Разберёмся?
Что такое логарифмическое уравнение? Примеры.
Как и намекает название, логарифмическое уравнение — это уравнение с логарифмами. Но не просто с логарифмами, а такое, где иксы находятся исключительно внутри логарифмов. И только там! Это крайне важно.
Иксы (чаще всего) встречаются в аргументе логарифма:
log2x = log23
log5(2x-1) = log5x
log4(x+1) = 3
lg(x2–5x+16) = 1
ln(x+3)+ln(x-5) = ln(3x-1)
Иксы иногда могут быть и в основании логарифма:
log2x+527 = 3
Или даже и там и там одновременно:
logx-1(x+5) = 2
Где угодно могут быть иксы. Лишь бы внутри логарифмов. Если, вдруг, в уравнении икс вылезет где-то снаружи, что-нибудь типа:
log3x = 11-x ,
то такое уравнение будет уже уравнением смешанного типа. Чётких правил решения такие уравнения не имеют, поэтому в этом уроке мы их рассматривать и не будем. Радуйтесь.)
Кстати, может попасться и такое уравнение, где внутри логарифмов сидят только числа. Например, такое:
3x+2 = lg400 — lg4
Что тут скажешь? Халява, если попалось такое! Ибо логарифм с числами — это просто какое-то число. Всего-навсего. Для расправы с таким монстром достаточно лишь знать свойства логарифмов. И всё. Каких-то специальных приёмов и правил, предназначенных именно для решения логарифмических уравнений, здесь не нужно.
Кстати, не следует думать, что внутри логарифмов могут стоять лишь линейные да квадратные выражения с иксами. Любые могут стоять. И дробные, и показательные, и тригонометрические — какие угодно, насколько позволяет фантазия составителей примера! Просто подавляющее большинство школьных заданий (процентов 90) — именно на линейные и квадратные выражения внутри логарифмов. Да и писать мне их проще, чем всякие там дроби, корни, синусы и прочую экзотику. Да и начинать знакомство обычно принято с самого простого.)
Итак, что такое логарифмическое уравнение — уяснили. Как же их решать?
Как решать логарифмические уравнения? Простейшие примеры.
Как уже говорилось выше, единого рецепта решения логарифмических уравнений на все случаи жизни в математике нет. Много их, уравнений. Самых разных…
Но волноваться не стоит. Ибо среди всего богатого многообразия логарифмических уравнений выделяются такие, решать которые очень и очень легко. В уме, фактически. Такие уравнения так и называются — простейшими. Именно с них и начнём. Для их решения желательно лишь иметь общее представление о логарифме вообще, не более того. Зачем? Гм… Согласитесь, как-то неловко браться за решение логарифмического уравнения, даже понятия не имея что такое логарифм… Самонадеянно, я бы сказал.)
Так что же это за уравнения?
Это уравнения типа:
log2x = log23
log5(2x-1) = log5x
log4(x+1) = 3
log2x+527 = 3
И так далее и тому подобное…
А теперь собираем волю в кулак и вникаем в простые вещи. В чём суть? Процесс любого (да-да, именно любого!) логарифмического уравнения заключается в переходе от уравнения с логарифмами к уравнению без них. В простейших уравнениях этот переход осуществляется всего за один шаг. На то они и простейшие.) Как именно? Это только на конкретных примерах показать можно.
Решаем первое уравнение по списку:
log2x = log23
Для решения этого крутого примера знать почти ничего и не надо, да. Обычная интуиция.) Что нам сильнее всего не нравится в этом примере? Что-что… Логарифмы не нравятся! Верно. Избавиться бы от них… Но как? Смотрим на пример. Смотрим и… прям таки хочется взять, да и выкинуть логарифмы вообще! А можно? Новость хорошая: да, можно! Математика не возражает.)
Убираем логарифмы и сразу получаем ответ:
х = 3
Здорово, правда? И, главное, просто и быстро! И так нужно поступать всегда. Выкидывание логарифмов подобным образом — ключевая идея решения любого логарифмического уравнения. Простого, сложного — неважно. В математике эта приятная операция (выкидывание логарифмов) носит своё специальное название — потенцирование. Но на такую ликвидацию есть набор жёстких правил. Перечислю их.
Убирать логарифмы (т.е. потенцировать) можно, если:
1. У них одинаковые основания;
2. Логарифмы слева и справа чистые и стоят в гордом одиночестве.
Разберёмся с этими двумя пунктиками поподробнее. Иначе потом эти пунктики будут жестоко мстить на контрольных и экзаменах.
Например, уравнение:
log2x = log0,52
Можно здесь убирать логарифмы? Нет! Основания разные: слева стоит логарифм по основанию 2, а справа — по основанию 0,5. Разные числа. А нужны — одинаковые. Не катит…
Или такой пример:
lgx + lg(x+1) = lg(x2+4)
Здесь тоже нельзя потенцировать уравнение. Пусть даже все три логарифма по одному основанию (десятке), но слева не одинокий логарифм, их там два.
Или такое:
log3(2x-1) = 2log3x
А вот здесь нельзя потенцировать по другой причине: двойка справа не позволяет. Коэффициент, понимаешь. Мелочь, а тем не менее существенная.) Правило — штука жёсткая.
Одним словом, убирать логарифмы можно тогда и только тогда, когда логарифмическое уравнение выглядит именно (и только!) вот так:
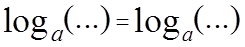
Основания "а" — одинаковые. Причём, даже не обязательно числовые. Могут быть с иксом, могут быть без икса — не суть. Важно, что одинаковые. А вот в скобках, на месте многоточий, могут стоять совершенно любые выражения с иксом — простые, сложные — какие угодно. Это неважно. Важно другое. А именно — то, что после ликвидации логарифмов у нас остаётся более простое уравнение без логарифмов. Конечно же, предполагается, что решать линейные, квадратные, дробные, показательные, иррациональные, тригонометрические и прочие уравнения без логарифмов вы уже умеете.
Теперь, вооружившись ценными познаниями, решаем следующий пример по списку:
log5(2x-1) = log5x
Все условия для потенцирования выполняются: основания одинаковые, логарифмы слева и справа чистые. Потенцируем и решаем простенькое линейное уравнение:
2x-1 = x
x = 1
Вот и всё.) Как видите, вся логарифмическая часть решения уравнения заключается только в ликвидации логарифмов. И всё! А дальше работаем с более простым линейным уравнением, уже без логарифмов. Элементарно.
Остальные уравнения из нашего списка уже так просто не решить. Здесь уже надо знать, что такое логарифм.
Например, типичное задание из ЕГЭ — это третье уравнение:
log4(x+1) = 3
Слева стоит логарифм от чего-то там, а справа — число. Вспоминаем элементарный смысл логарифма. А именно — то, что этот самый логарифм — это какое-то число, в которое надо возвести основание (т.е. четыре), чтобы получить аргумент логарифма (т.е. х+1).
Но это число нам известно! Оно равно трём! Прямо по нашему уравнению.)
Стало быть, имеем полное право записать:
43 = х+1
Всё. Логарифм исчез и осталось безобидное линейное уравнение:
64 = х+1
х = 63
Это уравнение мы решили, пользуясь только определением логарифма. Что, потенцированием решать проще? Да, согласен! Если вы умеете делать из числа логарифм по любому основанию, то никаких проблем. Если не умеете, читайте третий урок про логарифмы. Там всё популярно изложено.
Итак, перед нами то же самое уравнение:
log4(x+1) = 3
Для потенцирования нам необходимо добиться, чтобы в уравнении слева и справа стояли логарифмы по одному и тому же основанию. Для этого справа из тройки сделаем логарифм по основанию четыре. Как именно? По нашей старой доброй технологии, подробно описанной по ссылке выше.
Вот так:
3 = log443
Тогда получим следующее:
log4(x+1) = log443
Вот мы и получили то что хотели. Слева логарифм по основанию четыре, справа тоже. С чувством глубокого удовлетворения потенцируем и приходим к тому же самому ответу:
х+1 = 43
х+1 = 64
х = 63
Как видите, и так и сяк решать можно. Как хотите, так и решайте. Кому-то хватает простого определения логарифма, а кому-то удобно потенцирование. Как говорится, о вкусах не спорят. Ещё раз напоминаю, что умение делать из числа логарифм — весьма и весьма полезная штука в логарифмических уравнениях. И особенно — в неравенствах! Не пренебрегаем.)
И, наконец, последнее уравнение:
log2x+527 = 3
Здесь отличие от предыдущих примеров заключается в том, что икс стоит не в аргументе, а в основании логарифма. Ну и что? Решается уравнение совершенно аналогично, по определению логарифма:
(2х+5)3 = 27
2х+5 = 3
2х = -2
х = -1
И все дела.)
Кстати, попробуйте решить этот же пример через потенцирование. Удивитесь, но получите то же самое.)
Итак, с простейшими уравнениями всё предельно ясно. Работаем либо напрямую через потенцирование (если логарифмы слева и справа), либо по определению логарифма (если слева логарифм, а справа число).
А теперь рассмотрим несколько уравнений чуть посложнее. Таких, которые напрямую через ликвидацию логарифмов не решаются. Их сначала надо немного подготовить к ликвидации. Как готовить? Свойства логарифмов — вот он, ключевой рецепт!
Пользуемся свойствами логарифмов!
Проскакивала у нас выше парочка уравнений.
Например:
lgx + lg(x+1) = lg(x2+4)
Что делать? Убирать логарифмы пока нельзя, против правил будет: слева сумма логарифмов. А нужен — одинокий. Как выкрутиться? Да свойства логарифмов вспомнить! Мы же знаем, что сумму двух логарифмов всегда можно превратить в один логарифм, но от произведения. Если основания одинаковые, конечно.
Вот и превращаем по формуле:
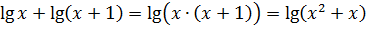
Вот и всё. Заменяем сумму логарифмов на логарифм произведения:
lg(x2+x) = lg(x2+4)
Что, десятичные логарифмы (lg) вас смущают? Зря! Ещё раз напоминаю, что базовые логарифмические формулы, операции и свойства распространяются на все виды логарифмов без исключения. Десятичные, натуральные, по основанию 13, по основанию "пи" — любые! Так что можно складывать логарифмы по формуле и потенцировать совершенно безболезненно. Лишь бы основание в процессе применения формул и перед потенцированием оставалось одинаковым. В нашем случае — десятка.
Смело потенцируем, решаем:
x2+x = x2+4
х = 4
Всё!
Запоминаем:
Десятичные (lg) и натуральные (ln) логарифмы ни по определению, ни по свойствам ничем не отличаются от обычных!
Ещё один примерчик:
log3(2x-1) = 2log3x
Опять же, потенцировать уравнение нельзя: справа нужен чистый логарифм, а двойка мешает. И снова нам на помощь приходят свойства логарифмов! Не нравится двойка? Подумаешь, проблема! А мы её внутрь логарифма спрячем.)
Вот так:
2log3x = log3x2
И все дела, логарифм от коэффициента "очистили".) А дальше — по накатанной колее, подставляем, потенцируем:
log3(2x-1) = log3x2
2х — 1 = х2
x2 — 2x + 1 = 0
Решаем простецкое квадратное уравнение и получаем единственный корень
х = 1
Как видите, тоже ничего сложного. Одно-два простых свойства логарифмов и — готово дело.) Но… бывают и сюрпризы, да. Например, некоторые ученики успешно решают уравнения, где только логарифмы, но зависают на уравнениях с постоянными числами.
Делаем логарифмы из постоянных чисел!
Например такое уравнение:
log2(3x-2) + 3 = log2(14x+1)
Куда пристегнуть тройку? Никуда не надо пристёгивать, надо снова из тройки логарифм сделать! По нашей излюбленной схеме:
3 = log223 = log28
А вот теперь логарифмические формулы в уравнении отлично идут!
log2(3x-2) + log28 = log2(14x+1)
log2(8(3x-2)) = log2(14x+1)
Убираем логарифмы и дорешиваем элементарщину:
8(3x-2) = 14x+1
24x-16 = 14x+1
10x = 17
x = 1,7
И всего делов-то. А вот без превращения тройки в логарифм это уравнение так просто не решилось бы!
Запоминаем:
Любое число (или даже выражение!) можно превратить в логарифм по любому основанию.
Разберём ещё один сюрприз. Это когда уравнение с виду простенькое, но основания логарифмов — разные.
Разные основания — что делать?
Например:
log9x + 2log3x = 5
Что, тупик? Складывать логарифмы по формуле нельзя, а уж убирать совсем — тем более. Основания не разрешают. Они… разные, да.) Тройка и девятка.
Вот и делаем их одинаковыми!
Классический метод — действия со степенями. В нашем случае проблема решается очень просто. Ибо из девятки тройку сделать (и наоборот) — пара пустяков. Ведь 9=32, не так ли? Про родню по степени помните?
А если вспомнить формулку, избавляющую нас от степени в основании
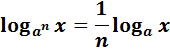
то совсем отлично получится:
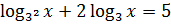
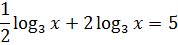
Воот. Основания выровняли. Правда, коэффициенты вылезли — ну и что? Можно, конечно, их внутрь логарифмов (в аргументы) степенями загнать и далее по формуле сложения свести всё к одному логарифму, но, может, есть способ попроще? Как вы думаете?
Да! Просто привести подобные, как с буквами! Логарифмы-то одинаковые.) А алгебра — штука универсальная, и ей неважно, логарифмы под буквами скрываются или синусы, яблоки, зарплата, время. Для неё это всегда будет 0,5а+2а = 2,5а.
Вот и пишем:
2,5log3x = 5
Остались пустяки — поделить на 2,5 (базовые преобразования никто не отменял) и решить простейшее уравнение:
log3x = 2
x = 9
Здесь нас, конечно же, спасла родня по тройке. А если основания не родственные? Скажем, не 3 и 9, а 3 и 7? Тогда, скорее всего, преобразования более хитрые. Но это — тема отдельного урока.)
Не забываем действия со степенями!
Вроде бы, столько долбим эти несчастные степени, а ступор у некоторых иногда случается. Как только приходится сталкиваться с отрицательными да дробными показателями…
Например, решали мы такое уравнение:
log4(x+1) = 3
Сейчас я поменяю в нём всего одно число. Вот такое уравнение теперь решим:
log4(x+1) = -0,5
И что теперь делать? С тройкой-то всё просто решалось, а тут -0,5. Как ни странно, делаем всё то же самое!
Прямо по смыслу логарифма пишем:
х+1 = 4-0,5
А вот тут многие и зависнут. Что такое степень 0,5? Да ещё и с минусом…
Что-что… Со степенями у вас проблемы — вот что! Коли такие вопросы волнуют в старших классах. Срочно повторить отрицательные и дробные показатели!
А кто со степенями в мире и согласии, тот лишь скупо улыбнётся и твёрдой рукой запишет:
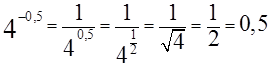
Дальше всё ясно:
х+1 = 0,5
х = -0,5
Что мы видим? Мы видим, что, каким бы ни было наше уравнение — простым, посложнее, суперсложным (о них в других уроках), мы всегда добиваемся одной и той же цели. А именно — чтобы слева и справа в уравнении стояли чистые логарифмы по одному и тому же основанию. Или ситуации "слева — чистый логарифм, справа - число". То есть, простейшего уравнения. А дальше — дело техники.
Итак, самое главное по простейшим уравнениям и уравнениям, сводящимся к оным.
Запоминаем:
1) Основной принцип решения простейших логарифмических уравнений — это потенцирование левой и правой частей (мысленная ликвидация логарифмов). Или решение через определение логарифма.
2) Простейшие логарифмические уравнения — это финишная прямая при решении любых других более сложных уравнений с логарифмами.
3) Любое сложное логарифмическое уравнение надо пробовать свести к простейшему (или к их комбинации). Либо базовыми тождественными преобразованиями уравнений, либо с помощью свойств логарифмов и действий со степенями.
А теперь, как всегда, набиваем руку на самых простых примерах.
Найдите корень или сумму корней (если их несколько) уравнений:
ln(3x+7) = ln(2x-1)
log2x = 5
log7(x2+28) = log7(11x)
lg(x2–5x+16) = 1
log0,1(3x+7) = -2
logx2 = 0,25
ln(e3+3x-6) = 3
Ответы (в беспорядке):
16; 32; 5; 2; 31; 8; 11
Получилось? Великолепно! Куда уж проще-то… Что? Число "е" смутило в последнем уравнении? А вы вспомните, что служит основанием натурального логарифма (ln) — и будет вам счастье.)
Примерчики посложнее (но ненамного). Здесь уже подключаем свойства логарифмов вкупе с тождественными преобразованиями уравнений.
Решить уравнения и найти сумму корней (если их несколько):
lg(x2+x+1) = 2lg(x+1)
log5(7x+4) — log5(2x-1) = 1
log4x + 3log2x = 7
log2(2x2–x+2) = log2x+2
Ответы (в беспорядке):
2,5; 3; 0; 4
И это вышло? Блеск! Значит, первую часть в решении логарифмических уравнений (хотя бы самых простых) вы уже освоили хорошо. Поздравляю! Осталось теперь разобраться со второй частью — и мы с вами будем уже во всеоружии. Можно будет и более хитрые примеры решать.)
Как видите, всё просто. Сводим уравнение к простейшему за один-два шага, выкидываем логарифмы, решаем себе и записываем ответ. Это хорошая новость.
А теперь — плохая новость. Успех в решении логарифмических уравнений этого урока вовсе не гарантирует вам успех в решении всех остальных уравнений. Даже простеньких на вид, подобных этим. Увы и ах…
Так в чём же дело? Это и есть та самая вторая часть решения логарифмических уравнений (любых!). И более того, я бы даже назвал это основной проблемой в решении логарифмических уравнений. Да и неравенств тоже.
Разберёмся с этой проблемой основательно! И решим её. Обязательно! В следующем уроке. Здесь ничего говорить не буду, дабы не рушить идиллию и не пугать народ.)
