Разложение на множители. Понятие и примеры.
Напоминаю, что тождественные преобразования выражений — основа всей математики. Превращение, шаг за шагом, страшного и неудобного выражения в белое и пушистое. Смысл любого тождественного преобразования — это запись математического выражения в другом виде c сохранением его сути. Кто не в теме — сходите по ссылке. Там всё предельно просто и доступно.)
Что такое разложение на множители? Всё элементарно. Прямо из самого названия. Можно не помнить (или не знать — кому как), что такое множитель, но то что это слово происходит от глагола "умножить" догадаться-то можно?)
Так вот:
Разложить на множители означает: представить исходное выражение в виде умножения чего-то на что-то.
И все дела. Надеюсь, математика и русский язык на меня не в обиде…)
Допустим, надо разложить число 18. Можно записать:
18=2·9
Вот мы и разложили число 18 на множители. Представили 18 в виде умножения 2 на 9. Обратите внимание, что циферки справа (2 и 9) совсем другие, нежели слева (1 и 8). Но при этом мы прекрасно понимаем, что 18 и 2·9 — одно и то же. Суть числа 18 от преобразования не изменилась.
А можно ли разложить 18 по-другому? Можно! Например:
18 = 2·9 = 3·6 = 2·3·3 = 0,5·36 = 1,5·12 = 4·3,5 = …….
Вариантов разложения — бесчисленное множество.
Зачем раскладывать на множители? Вопрос философский. Просто так — незачем, конечно. Но есть в математике темы, где без разложения на множители не обойтись. Ну вот прям никак…) Если говорить о числовых выражениях, то, прежде всего, это сокращение дробей и действия с корнями.
Например, задание:
Вычислить:
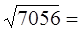
Пример не подарок, прямо скажем. Как из такого здоровенного числа корень извлекать? Без калькулятора! Да и извлечётся ли он нацело? Непонятно… Зато, если разложить число 7056 на множители, да сгруппировать в кучки одинаковые, жизнь-то наладится!
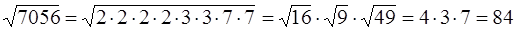
И калькулятора не понадобилось!)
Но числовые выражения — ещё полдела. А вот разложение на множители алгебраических (т.е. буквенных) выражений — штука не просто полезная, она — необходимая! Сомневаетесь? Напрасно. Чисто для примера:
Упростить выражение:
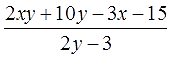
Кто не в теме, как раскладывать на множители, решить этот пример не сможет. А кто в теме, упрощает и получает:
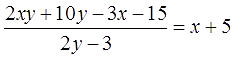
Класс, правда?) Кстати, решение довольно простое. Ниже сами увидите. Или, к примеру, такое задание:
Решить уравнение:
x10-x9=0
Страшно? Решается в уме, между прочим! С помощью разложения на множители. Ответ: x=0; x=1.
А если уравнение заменить на неравенство? Например:
x10-x9<0
Задание другое, но первый шаг решения всё равно тот же самый! Один в один. Разложение на множители.
Ответ: x ∈ (0; 1)
Чуть ниже мы разберём оба этих примера.
Или другой пример, для старшеклассников:
Решить уравнение:
lg10x - lg9x =0
Что, внушает? А вы не бойтесь! Читайте дальше и увидите, как всё просто! Ответ будет такой:
x=0; x=10
На этих примерах я показал основную цель разложения на множители. А именно — упрощение выражений и решение некоторых типов уравнений и неравенств.
Практические советы:
1. Если перед нами сложное дробное выражение, то можно попробовать разложить числитель и знаменатель на множители. Очень часто дробь сокращается и упрощается.
2. Если перед нами злое уравнение или неравенство, где слева — что-то страшное, а справа — ноль, то можно попытаться разложить левую часть на множители. Чаще всего это проясняет ситуацию.
Как раскладывать на множители? Основные способы разложения.
Итак, вот они:
1. Вынесение общего множителя за скобки;
2. Группировка;
3. Формулы сокращённого умножения;
4. Разложение квадратного трёхчлена.
Прошу запомнить этот джентльменский набор! Причём именно в таком порядке. Это важно. Все замороченные примеры имеет смысл проверять на все возможные способы разложения. От простого к сложному. Что-то работает, что-то нет. Это нормально.)
Вот и мы начнём. По порядочку. Итак!
1. Вынесение общего множителя за скобки
Самый простой и в то же время самый распространённый способ. Хуже никогда не делает. Делает либо лучше, либо никак.) Потому и стоит первым пунктом.
Все вы знаете (уж я-то надеюсь!) распределительный закон умножения:
a(b+c) = ab+ac
Или, если слагаемых несколько:
a(b+c+d+…) = ab+ac+ad+…
Все равенства в математике работают в обоих направлениях. Как слева направо, так и справа налево. Имеем полное право записать:
ab+ac = a(b+c)
Или:
ab+ac+ad+… = a(b+c+d+…)
Что происходит при такой записи? Слева буковка а — общий множитель для всех слагаемых. Умножается на всё что есть. А справа это самое а находится уже за скобками. Вот и вся суть вынесения общего множителя за скобки.
Практическое применение способа рассмотрим на примерах. Сначала пример совсем примитивный. Но на этом примитивном примере я покажу самые важные моменты для любого разложения на множители. Итак, вникаем.
Разложить на множители:
ху+10у
Какой общий множитель сидит в обоих слагаемых? Игрек, конечно! Его и будем выносить за скобки. Делается это так. Сразу пишем игрек за скобками:
ху+10у = y(….
А в скобках пишем результат деления каждого слагаемого на этот самый игрек. По порядочку. Вот так:
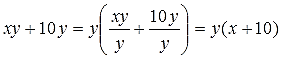
И все дела.) Разумеется, так подробно расписывать не нужно. Это действие в уме делается. Но понимать, что, как и откуда крайне желательно.
Фиксируем в голове:
При вынесении пишем общий множитель за скобками. В скобках пишем результат деления каждого слагаемого на этот самый общий множитель. Поочерёдно.
Вот мы и разложили выражение ху+10у на множители. Превратили его в умножение игрека на (х+10). Кстати, обращаю ваше внимание, что исходное выражение тоже содержало в себе умножение. Даже два: x·y и 10·y. Но оно не было разложено на множители! Почему? Потому, что в исходном выражении, помимо умножения, было ещё и сложение, знак "+"! А выражении y(x+10) — только умножение! Почувствуйте разницу!
"Стоп-стоп! Но ведь в скобках по-прежнему есть сложение!" — слышу я недовольные возгласы…
Да. Внутри скобок есть сложение. Но весь фокус в том, что пока скобки не раскрыты, мы рассматриваем их как одну букву. И все действия со скобками делаем целиком, как с одной буквой! С этой точки зрения в выражении y(x+10) кроме умножения ничего нет.
Кстати, насчёт раскрытия скобок! А как проверить, всё ли мы правильно сделали? Элементарно! Достаточно заново раскрыть скобки, т.е. обратно помножить на скобки то что вынесли. И посмотреть, получилось ли исходное выражение?
Смотрим:
y(x+10) = xy+10y
Всё путём!)
Этот-то пример совсем простецкий, чисто для знакомства. Но если слагаемых несколько, да с разными знаками, то "ашипки" сыплются как из рога изобилия!
Запоминаем простую вещь:
При необходимости проверяем результат разложения обратным перемножением.
Усложняем задачу.
Разложить на множители:
2ху+10у
Ищем общий множитель. Ну, с игреком всё ясно, его можно вынести. А есть ли ещё общий множитель? Есть! Это двойка. Можно ведь записать наше выражение вот как:
2ху+10у=2xy+2·5y
Теперь видно, что общим множителем будет 2y. Именно его и выносим:
2ху+10у = 2y(x+5)
Разложили.)
Кстати, а что будет, если вынести только игрек? Да ничего необычного:
2ху+10у = y(2x+10)
Это тоже будет разложением на множители. Но в этом увлекательном процессе принято раскладывать всё до упора, пока есть такая возможность. В данном случае в скобках можно вынести двойку:
y(2x+10) = 2y(x+5)
Как видите, всё то же самое, только с одним лишним действием. Посему запоминаем:
При вынесении общего множителя за скобки стремимся вынести максимально возможный общий множитель.
Продолжаем наши игры?
Разложить на множители:
2xy+10y–3x–15
Что будем выносить? Двойку? Икс? Игрек? Не-а.) Не катит. Напоминаю, что выносить за скобки можно только общий множитель. Тот, который сидит во всех слагаемых без исключения. На то он и общий. Здесь такого множителя нету… Что, можно не раскладывать? Ну да, рано обрадовались.)
Знакомимся!
2. Группировка
Строго говоря, группировка не является самостоятельным способом разложения на множители. Скорее, это продвинутый метод вынесения общего множителя за скобки для более крутых примеров. В чём суть: надо сгруппировать слагаемые так, чтобы всё получилось. Словами это не описать, только на конкретном примере показать можно.
Итак, перед нами выражение:
2xy+10y–3x–15
Видно, что какие-то общие числа и буквы имеются. Но! Общего множителя, который был бы во всех слагаемых, нет! Что делать?
Хладнокровно игнорируем этот жуткий факт. Поступаем красиво и элегантно. Разбиваем выражение на кусочки! Или — группируем. Как разбиваем? Элементарно! Ставим скобки. Например, можно так:
2xy+10y–3x–15 = (2xy+10y)–(3x+15)
Вот здесь всплывает частый ляп. Обратите внимание на вторые скобки! Перед ними стоит знак минус, но слагаемые 3x и 15 внутри скобок стали с плюсом. Если обратно раскрыть скобки, то знаки поменяются и мы получим исходное выражение. Т.е. суть исходного выражения от скобок не изменилась.
Но если вы просто взяли и воткнули скобки, не учитывая смену знака, например вот так:
2xy+10y–3x–15 = (2xy+10y) — (3x–15) ,
то это будет грубейшей ошибкой. Справа — уже другое выражение. Раскройте скобки и всё станет ясно. Дальше решать нет смысла, да…
Но вернёмся к разложению на множители. Итак, с помощью скобок мы разбили исходное выражение на две группы. Такое, казалось бы, надуманное действие приводит (иногда) к потрясным результатам! Смотрим на первые скобки (2xy+10y) и соображаем, что можно вынести. Ну, этот пример мы выше уже решили. Можно вынести 2у:
(2xy+10y) = 2y(x+5)
А теперь изучаем вторые скобки (3x+15). Здесь можно вынести тройку:
(3x+15) = 3(x+5)
Всё наше выражение будет выглядеть вот так:
(2xy+10y)–(3x+15) = 2y(x+5)–3(x+5)
Разложили на множители? Нет. Напоминаю, что в результате разложения должно получиться только умножение. А у нас знак минус торчит посерёдке, всё портит… Но! В обоих слагаемых есть общий множитель! Это (x+5). Я не зря говорил, что скобки целиком — это единое цельное выражение, которое можно рассматривать как одну букву. Значит, эти скобки можно… вынести за скобки.) Да, именно так!
Выносим (x+5) за скобки. В скобках пишем результат деления каждого слагаемого на (x+5). Получится:
2y(x+5)–3(x+5) = (x+5)(2y-3)
Всё! Вот теперь в нашем выражении кроме умножения ничего нет. Значит, разложение на множители увенчалось успехом. Вот так оно выглядит:
2xy+10y–3x–15 = (x+5)(2y-3)
Итак, запоминаем суть группировки:
Если в исходном выражении нет общего множителя, разбиваем выражение скобками так, чтобы внутри каждой скобки общий множитель ИМЕЛСЯ. Выносим его для каждой из скобок и смотрим, что получилось. Если повезло и в скобках остались совершенно одинаковые выражения, то выносим эти скобки за скобки.
Но не так всё просто. Может и не повезти. Группировка — процесс творческий. Не всегда с первого раза получается. Иногда приходится всячески хитрить: пробовать другую комбинацию, менять слагаемые местами или даже добавлять слагаемые. Главное — не падать духом!
Поучительный пример:
Разложить на множители:
х2+3xy+2y2
С чего начинать? Общего множителя явно нет, выносить за скобки нечего. Группировка также не катит: три слагаемых красиво не сгруппируешь. Но! Если расписать 3xy как сумму 2xy+xy, (т.е. разбить одно из слагаемых на два), всё получится! Смотрите!
х2+3xy+2y2 = х2+2xy+xy+2y2 = (х2+2xy)+(xy+2y2)
Как я додумался именно до такого разбиения? Открываю секрет. Я посмотрел на исходный пример и поприкидывал. Примерно так:
"Так, значит… С ходу не группируется, слагаемых — три, одно остаётся без пары. Хотя бы четыре для группировки нужно. Да и коэффициенты не ахти. Придётся выкручиваться и какое-то слагаемое разбивать на два. Но какое? Для удачной группировки важно иметь как можно больше одинаковых значков и как можно меньше - разных! Посмотрю-как я на коэффициенты! Надо же за что-то цепляться, искать хоть что-то общее!
При х2 я вижу единичку. А при y2 — двойку. У среднего же члена, 3xy, вместо тройки тоже хотелось бы единичку и двойку получить. Чтобы числа стали хоть как-то похожи друг на друга, было что с чем сгруппировать. Как из тройки сделать единичку и двойку? Расписать 3xy как 2xy+xy!
Получится: х2+3xy+2y2 = х2+2xy+xy+2y2 = (х2+2xy)+(xy+2y2)"
Верные мысли! Теперь коэффициенты в каждой группе — только единичка и двойка. Дальше всё ясно. В первых скобках выносим икс, во вторых — игрек. Будет:
(х2+2xy)+(xy+2y2) = x(x+2y)+y(x+2y)
О! В скобках — одинаковые выражения! Йес!!!
x(x+2y)+y(x+2y) = (x+2y)(x+y)
Ура! Разложили! Вот что получилось:
х2+3xy+2y2 = (x+2y)(x+y)
Вот такой финт ушами.)
Запоминаем секретный приёмчик:
Если многочлен содержит нечётное число слагаемых (три, пять и т.д.), то можно попробовать разбить одно (или несколько) слагаемых на два. Так, чтобы всё сгруппировалось. И зацепкой (что и как разбивать) будут служить коэффициенты при оставшихся членах. Разбивать члены надо так, чтобы получить как можно больше одинаковых коэффициентов в примере.
Примеры заданий
А теперь, набравшись полезных знаний, можно и злые примеры порешать. Была у нас в начале урока четвёрка таких.
Упростить выражение:
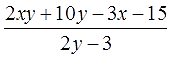
По сути, пример этот мы уже разобрали. Незаметно для себя.) Ещё раз напоминаю: если перед нами жуткая дробь, первым делом пробуем разложить числитель и знаменатель на множители. Других вариантов упрощения просто нет.
Ну, со знаменателем всё ясно, он никак не раскладывается. А числитель? Числитель мы уже разложили в параграфе про группировку! Вот так:
2xy+10y–3x–15 = (x+5)(2y-3)
Вставляем результат разложения в числитель дроби:
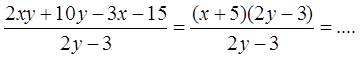
Основное свойство дроби помните? По правилу сокращения дробей, мы имеем право разделить (одновременно!) числитель и знаменатель на одно и то же число или выражение. Дробь от этого не изменится. Вот и делим и числитель и знаменатель на выражение (2y-3). В числителе останется (x+5), а в знаменателе — единичка. А если в знаменателе единичка, то этот знаменатель можно и вовсе не писать. Продолжаем:
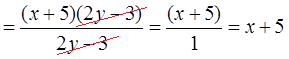
Окончательный результат упрощения:
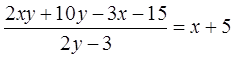
И все дела.) Особо хочу подчеркнуть, что сокращение дроби возможно тогда и только тогда, когда и в числителе и в знаменателе только умножение! Именно поэтому разложение алгебраических выражений на множители так важно для упрощения. Разумеется, если множители сверху и снизу разные, то и не сократится ничего. Всяко бывает. Но разложение на множители даёт шанс! Намёк понятен?)
Следующий пример, с уравнением:
Решить уравнение:
x10-x9=0
Тут и думать нечего. Выносим общий множитель x9 за скобки. Получится:
x9(x-1)=0
Осталось догадаться, что произведение множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю. Что, сомневаетесь? Тогда предъявите мне два ненулевых числа, которые в произведении ноль дадут.) Не получается? То-то… Вот и приравниваем к нулю, сначала первый множитель:
x9=0
Ну и какое число в девятой степени ноль даст? Только ноль! Никакое другое… Поэтому:
х=0
Один корень нашли. Разбираемся со вторым множителем:
x-1=0
x=1
Вот вам и ответ: x1=0; x2=1. Два корня. Оба подходят к нашему уравнению. Переходим к следующему примеру, меняем уравнение на неравенство.
Решить неравенство:
x10-x9<0
С неравенством возни чуть поболее будет, но первая часть решения та же самая. Слева — выражение, справа — ноль. Раскладываем левую часть на множители:
x9(x-1)<0
А дальше — стандартный алгоритм метода интервалов. Расписывать детально не буду, это тема отдельного урока. Кто знает, и так поймёт. Делаем из неравенства уравнение, решаем его и получаем те же самые два корня.
x9(x-1)=0
x1=0; x2=1
Чертим числовую ось, отмечаем точками найденные корни. Неравенство строгое, соответственно обе точки будут выколотыми. Ставим знаки +/- в соответствии с исходным выражением и рисуем старую добрую "змейку". Получаем картинку:
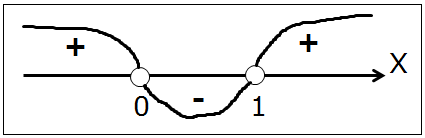
Смотрим на знак неравенства. Нас интересует минусовая область иксов. Смело пишем:
Ответ: x ∈ (0; 1)
Пример для старшеклассников:
Решить уравнение:
lg10x - lg9x =0
Чем-то похоже на предыдущие примеры, правда? Совершенно верно. Та же песня! Разложение на множители.) Страшные значки lg пусть вас не смущают, базовые преобразования (а разложение на множители — именно одно из базовых преобразований) работают во всей математике! Смело выносим общий множитель lg9x за скобки:
lg9x(lgx — 1) =0
Дальше всё как в предыдущем примере:
lg9x=0
lgx=0
x=1
Это первый корень. Переходим ко второму множителю:
lgx — 1=0
lgx=1
x=10
Вот и ответ готов: x1=1; x2=10
Кстати, обратите внимание на один важный момент в решении уравнений! После разложения на множители мы решаем уравнение по кусочкам! Каждый множитель приравниваем к нулю отдельно. Это означает, что если у нас будет не два множителя, а три, пять, да хоть двадцать пять, то решать будем аналогично. По кусочкам.
Например:
x2(x+1)(x-2)(x+3)(x-4)=0
Кто раскроет скобки, перемножит всё и приведёт подобные, тот навсегда зависнет на этом уравнении. Мартышкин труд.) Наблюдательный ученик сразу увидит, что слева — произведение, а справа — ноль. И начнёт поочерёдно приравнивать к нулю каждый множитель. И за 10 секунд получит (в уме!) верный ответ:
x1=0; x2=-1 x3=2; x4=-3; x5=4
Красиво, правда? Такое простое и элегантное решение возможно только если левая часть разложена на множители! Вот и весь секрет.)
Как решать нестандартные примеры? ОДЗ и прочие подводные камни.
Ну и на десерт рассмотрим слегка нестандартный примерчик на ту же тему. Который по шаблону не решается, или решается легко, но… неправильно.
Например, такое уравнение:
xlgx–x+lgx–1 =0
Что здесь необычного? Да. Это уравнение смешанного типа. Иксы стоят как внутри логарифмов, так и просто так. К сожалению, аналитически такие уравнения, как правило, не решаются вовсе. На 99%. Зато оставшемуся одному проценту самое место в этом уроке! Почему? А потому, что именно разложение на множители даёт нам шанс разделить разные типы переменных!
В чём суть? Нужно добиться, чтобы после разложения разные типы переменных разошлись по разным множителям! Логарифмы отдельно, а иксы без логарифмов — отдельно. Вот и раскладываем. Кто освоил группировку, тот даже не заметит трудностей. Группируем, получаем:
(xlgx-x)+(lgx-1)=0
x(lgx-1)+(lgx-1)=0
(lgx-1)(x+1)=0
Вот так. Как говорится, мухи отдельно, котлеты — отдельно. :) Теперь слева произведение, справа — ноль. Можно приравнивать к нулю каждый множитель по порядочку. Независимо друг от друга.
Для первых скобок, решая простейшее логарифмическое уравнение, получим:
lgx-1=0
lgx=1
x=10
Для вторых скобок получим:
x+1=0
x=-1
Получили два корня. Рука уже тянется к бумаге, но… Разумеется, думать и держать в голове всю остальную математику (ОДЗ и прочие хитрые штучки) никто не отменял, да.)
Ответ в виде:
x1=-1; x2=10
это неверный ответ! Окончательный корень — один. А именно:
x=10
В чём же дело? Вы правы. Дело в ОДЗ, да.) Но сначала вскрою проблемку на более глубоком уровне. Дело всё в том, что так горячо любимое всеми школьниками заклинание: "Произведение равно нулю, когда хотя бы один из множителей равен нулю" — строго говоря, неверное, да…) Точнее, неполное. Это и приводит к подобным промахам.
А полная и строгая форма звучит вот как:
Произведение равно нулю, тогда и только тогда, когда хотя бы один из множителей равен нулю, а остальные при этом НЕ ТЕРЯЮТ СМЫСЛА.
А в нашем примере при x=-1 множитель (х+1) обнуляется, но множитель (lgx-1) теряет смысл! Не существует логарифмов от отрицательных чисел, да…) Так что всё честно.
Поэтому, чтобы такого не было, перед решением данного уравнения надо сразу записывать ОДЗ. А именно — аргумент логарифма, где бы он ни стоял, должен быть всегда строго больше нуля:
x>0
Забыли? Значит, имеются пробелы в знаниях о логарифмах. Гуляйте по ссылочке.)
Вот теперь записанная ОДЗ сразу снимает все вопросы! Смотрим на наши иксы. Первый корень x=10 нас (и ОДЗ) вполне устраивает: десятка больше нуля. А вот второй, x=-1, никуда не годится. Минус один меньше нуля. ОДЗ — штука бескомпромиссная.
Ответ: x=10
Полезные советы:
1. Если перед вами нестандартное уравнение смешанного типа, первым делом пробуем разделить разные типы переменных. Чаще всего с помощью разложения на множители.
2. Вне зависимости от типа уравнения, прежде всего записываем ОДЗ, если это необходимо. Это убережёт от досадных и обидных ляпов в виде посторонних корней на 100%.
Надеюсь, вы ощутили весь потенциал разложения на множители. Мощная штука, правда?
В этом уроке мы поговорили о вынесении общего множителя за скобки и о группировке. Осталось рассмотреть формулы сокращённого умножения и разложение квадратного трёхчлена. Это — темы отдельных уроков.
