Арифметическая прогрессия — это очень и очень простое понятие. И это отнюдь не пустые слова с сомнительной целью утешить, успокоить и приободрить слабо подготовленного ученика. Арифметическая прогрессия — это и вправду просто! Всё-таки сомневаетесь? Напрасно! Чуть ниже сами убедитесь. Если рискнёте и… почитаете.)
В этом небольшом уроке вы:
а) прочувствуете и поймёте смысл арифметической прогрессии;
б) ознакомитесь и разберётесь с базовыми терминами и обозначениями, относящимися к арифметической прогрессии;
в) научитесь решать простенькие задачки по арифметической прогрессии.
Ну что, трогаемся в путь?)
Наше знакомство с прогрессиями (и арифметической — в том числе) мы начнём… нет, не со строгого определения арифметической прогрессии! А начнём мы с такого ключевого понятия, как последовательность.
Числовые последовательности, знакомство.
В житейском плане слово «последовательность» вопросов, как правило, ни у кого не вызывает. Это длинное слово всего лишь означает, что что-то следует за чем-то. Например, последовательность действий, последовательность событий, последовательность дней недели, времён года и так далее.
Или когда кто-то следует за кем-то. Например, последовательность людей в очереди. Или последовательность коров на тропе к водопою.)
Из чего состоит любая последовательность? Тут тоже всё логично. Если идёт речь о последовательности дней календаря, то из дней, если об очереди покупателей на кассе, то — из покупателей. И так далее.)
Но… математика — наука строгая. По законам природы устроена. И работает со всеми объектами сразу. Поэтому ей должно быть без разницы, что (или кто) под этими объектами скрывается — дни, покупатели, спортсмены, коровы, свиньи… Для неё всё едино: последовательность — и всё тут.) Как можно одним словом описать любой объект, из которого состоит любая последовательность? Очень просто: член последовательности! И всё.) Кратко и точно!
Под ёмким словом «член» скрываются все объекты всех последовательностей махом — и дни, и месяцы, и покупатели, и коровы, и гуси — всё что угодно! Вот из каких объектов конкретная последовательность состоит, те объекты и являются её членами.
Например, если идёт речь о последовательности календарных месяцев, то январь — член этой последовательности. И июнь — член. И ноябрь — тоже член, да.)
Математика, как правило, работает с числовыми последовательностями. Что это за зверь? Всё просто, как в сказке. Это последовательность, членами которой являются числа. Совершенно любые! Целые, дробные, отрицательные, иррациональные — какие угодно!
Например, последовательность натуральных чётных чисел:
2, 4, 6, 8, 10, 12, 14, 16, …
Или последовательность цифр в десятичной записи числа "пи":
3, 1, 4, 1, 5, 9, 2, 6, …
И так далее. Насочинять и понаписать можно всё что угодно, даже вообще безо всякой логики. Что-нибудь типа:
-2; 0; -0,12; 33; 7; -1,2; …
Как вы видите, в некоторых последовательностях имеется какая-то закономерность, а в некоторых — нет. Всё зависит от моей (или вашей) фантазии.)
Последовательности (в том числе и числовые, да) бывают конечные и бесконечные. Вышеприведённые примеры — это примеры бесконечных числовых последовательностей. С неограниченным количеством членов.
А вот последовательность, скажем, месяцев в году — конечна. Ибо количество членов в ней, как можно догадаться, равно 12. То есть, конечному числу.
Или, например, последовательность натуральных двузначных чисел, делящихся на три:
12, 15, 18, 21, …, 99.
Эта последовательность — тоже конечна, да.) Ибо первый член этой последовательности — это число 12, а последний член — это число 99. А вот дальше идут уже трёхзначные числа…
Приводя примеры самых разных последовательностей, я периодически употреблял слова: «первый член», «последний член», «количество членов»… Не задумывались, почему? Ответ прост: каждый член последовательности (любой!) стоит на своём месте! Всегда. Есть первый член, есть десятый, есть тридцать пятый — и так далее… Нумерация членов — строго по порядку! Без пропусков. Если же какие-то члены переставить местами (хотя бы два), то получится, вообще говоря, уже другая последовательность. Со своими правилами и порядками, да…
Одним словом, любая числовая последовательность — это упорядоченный (или занумерованный) набор чисел. И всё.
Понятие последовательности — более широкое, нежели пока малоизвестное нам понятие прогрессии (неважно, арифметической или геометрической). Ибо каждая прогрессия — это последовательность чисел, но не каждая последовательность чисел — это прогрессия. Как говорится, всякая селёдка — рыба, но не всякая рыба — селёдка.)
Более подробно и широко свойства и поведение самых разных (и, чего скрывать, порой очень интересных и необычных) числовых последовательностей изучается уже в ВУЗе, в курсе матанализа. В школе же изучаются лишь две самые простые их разновидности. Это, как вы уже, наверное, догадались, арифметическая и геометрическая прогрессии.
Арифметическая прогрессия попроще будет. Так что именно с неё и начнём.
Что такое арифметическая прогрессия? Понятие арифметической прогрессии.
Начнём наше знакомство, как обычно, с самого элементарного и примитивного. Для начала я запишу незаконченную последовательность чисел:
1, 2, 3, 4, 5, …
Сможете назвать, какие числа пойдут дальше, вслед за пятёркой? Любой э-э-э-э… в общем, даже человек, далёкий от математики, догадается, что дальше пойдут числа 6, 7, 8 и так далее.)
Что ж, ладно. Усложняю задачу. Даю незаконченную последовательность чисел:
1, 4, 7, 10, 13, …
Сможете уловить закономерность, продлить последовательность и назвать девятый её член?
Если вы сообразили, что это число 25, то примите мои поздравления! Ибо это означает, что вы не только прочувствовали ключевые моменты арифметической прогрессии, но и с блеском употребили их в дело! Если же не сообразили и не прочувствовали, то… читаем дальше.
А теперь переведём ключевые моменты из ощущений в математику.
Ключевой момент №1
Арифметическая прогрессия имеет дело с последовательностями чисел. Собственно, именно это больше всего и смущает поначалу. Ибо непривычно, да… Мы же с вами привыкли уравнения с неравенствами решать, графики строить… А тут — продлить последовательность. Найти член последовательности…
Ничего страшного. Просто последовательности (и прогрессии тоже) — это первое знакомство с новым разделом математики. Раздел называется «Ряды» и работает именно с последовательностями, с рядами чисел и даже выражений. Так что привыкаем.)
Ключевой момент №2
В любой арифметической прогрессии каждый её член отличается от предыдущего на одну и ту же величину. Всегда!
В первом примере эта величина — единичка. Какой член последовательности ни возьми, он больше предыдущего на единичку.
Во втором примере эта величина — тройка: каждый член больше предыдущего на тройку.
Собственно, именно этот момент и даёт нам возможность уловить закономерность и рассчитать все последующие числа.)
Ключевой момент №3
А вот этот момент не сразу бросается в глаза, да… Но он не менее важен. А именно: каждый член арифметической прогрессии стоит на своём месте. Как и в любой числовой последовательности, да. Есть первый член, есть пятый, есть сорок седьмой, и т.д. Если хотя бы два члена в последовательности переставить местами, то закономерность исчезнет. Вместе с ней, естественно, исчезнет и арифметическая прогрессия. Останется просто последовательность чисел.
Вот и всё. Вот и вся суть арифметической прогрессии.
Базовые термины и обозначения.
А вот теперь, вооружившись самыми начальными знаниями о последовательностях вообще и о ключевых моментах арифметической прогрессии в частности, можно и математическое определение арифметической прогрессии дать. Ибо, если я бы начал наш урок сразу с него, то арифметическая прогрессия для многих навсегда так и осталась бы монстром в тумане…
Итак!
Определение арифметической прогрессии.
Арифметическая прогрессия — это числовая последовательность, каждый член которой, начиная со второго, отличается от предыдущего члена на одну и ту же величину.
Вот и всё определение. После предыдущего параграфа, всё должно быть понятно и прозрачно, я надеюсь. Но на некоторых отдельных словах из определения я всё-таки заострю особое внимание.
Во-первых, слово "последовательность".
Запоминаем: арифметическая прогрессия — это именно числовая последовательность. А вовсе не ряд, как ошибочно любят её называть очень многие учителя и даже авторы учебников (наверное, для краткости). Что потом неизбежно приводит к путанице терминов и каше в голове уже у студентов, изучающих высшую математику.
В чём же дело? А вот в чём. Да, на обывательском уровне понятия "последовательность" и "ряд" - почти синонимы. Типа "последовательность покупателей". Или "ряд солдат". Но! В математике словом "ряд" именуется совершенно другое понятие. Хотя и неразрывно связанное с последовательностью, которая, как раз, этот самый ряд и образует.
Что такое ряд, в этом уроке не скажу! Маленькие ещё.) Сдадите ЕГЭ, поступите в ВУЗ — сами узнаете.) Но в изложении материала я буду строг. И не поленюсь, когда требуется, написать "последовательность чисел" вместо даже "ряд чисел" и уж, тем более, "числовой ряд". Длиннее, но зато более корректно. И никакой путаницы не будет. Привыкаем.)
Во-вторых, возможно, вы также обратили внимание на слова "начиная со второго" и "отличается от предыдущего". Здесь всё проще. Каждый член арифметической прогрессии на какую-то величину отличается от предыдущего члена. Десятый член отличается от девятого, второй член отличается от первого. А что можно сказать про самый первый член? На какую величину он отличается от предыдущего? А ни на какую!) Ибо у первого члена просто-напросто нет предыдущего. Вот и весь смысл этих слов. Именно поэтому говорить об "отличии от предыдущего" имеет смысл только начиная со второго члена включительно.)
В-третьих, есть ещё слова "на одну и ту же величину". Эта самая величина носит своё специальное название — разность арифметической прогрессии. К ней и переходим.)
Разность арифметической прогрессии.
Здесь всё просто.
Разность арифметической прогрессии — это число (или величина), на которое каждый член прогрессии больше предыдущего.
Ключевым словом, на которое следует обратить внимание в этом определении, является слово "больше". Математически этот факт означает, что каждый член арифметической прогрессии получается прибавлением разности прогрессии к предыдущему члену.
Поясняю.
Для расчёта, скажем, второго члена, надо разность прогрессии прибавить к первому члену. Для расчёта восьмого члена, надо разность прибавить к седьмому члену.
И так далее, и тому подобное…
Разность арифметической прогрессии может при этом быть какой угодно. Совершенно любой!
Разность может быть положительной. Тогда каждый член прогрессии получается и вправду больше предыдущего.
Например:
1, 4, 7, 10, 13, …
Здесь каждый член получается прибавлением положительного числа +3 к предыдущему члену. Такая прогрессия называется возрастающей.
Также разность может быть и отрицательной. Тогда каждый член прогрессии получается меньше предыдущего. Такая прогрессия называется убывающей.
Например:
1, -2, -5, -8, -11, …
Здесь каждый член получается тоже прибавлением к предыдущему члену, но уже отрицательного числа -3.
И, наконец, разность прогрессии может быть даже… равной нулю! Да-да! А почему — нет?
Например:
2, 2, 2, 2, 2, …
Всё то же самое. Каждый член прогрессии получается прибавлением к предыдущему члену числа 0.
Такие прогрессии и не возрастают и не убывают. Мы с вами их рассматривать не будем, ибо никакого практического интереса они не представляют. Но для общего развития знать об их существовании полезно. Скажем, зададут вам вопрос на засыпку: "Может ли арифметическая прогрессия состоять из одинаковых членов?" А вы уже знаете: может! Запросто.)
Кстати говоря, при работе с арифметической прогрессией бывает очень полезным сразу определить её тип — возрастающая она или убывающая. Это позволяет на раннем этапе сориентироваться в решении, засечь свои ошибки и исправить их, пока не поздно.)
Разность арифметической прогрессии обозначается, чаще всего, буковкой d.
Как найти это самое d ? Элементарно! Надо от любого числа прогрессии отнять предыдущее число. Отнять — значит, вычесть. Кстати, результат вычитания так и называется — "разность". Отсюда и название "разность прогрессии" для буковки d.)
Определим, например, величину d для возрастающей арифметической прогрессии:
3, 5, 7, 9, 11, 13, …
Всё просто, как в сказке. Берём любое число последовательности. Какое хотим, такое и берём. Например, 9. И отнимаем предыдущее число. То есть, 7.
Получаем:
d = 9 — 7 = 2
Вот и всё. Это правильный ответ. Для данной арифметической прогрессии разность равна двум.
Найдём теперь разность d для убывающей арифметической прогрессии. Например, вот такой:
1, -2, -5, -8, -11, …
Всё то же самое. Вне зависимости от знаков самих членов, снова просто берём любое число последовательности (например, -11) и отнимаем предыдущее число (т.е. -8).
Получим:
d = -11 — (-8) = -11 + 8 = -3
И все дела.) В этот раз разность прогрессии оказалась отрицательной. Что неудивительно, ибо наша прогрессия — убывающая.)
Как вы, возможно, заметили, брать можно совершенно любое число в последовательности. Хоть где-нибудь в начале, хоть в конце, хоть в серединке. Нельзя брать только самое первое число. По той простой причине, что у самого первого числа нет предыдущего.
Как обозначать арифметическую прогрессию?
Любое число в арифметической прогрессии, как мы помним, называется её членом.
Каждый член арифметической прогрессии, в свою очередь, обязательно имеет свой номер. Причём все номера идут строго по порядку, без пропусков: первый, второй, третий, четвёртый, пятый и так далее.
Например, в прогрессии
1, 4, 7, 10, 13, …
единичка — это первый член, четвёрка — второй, десятка — четвёртый… И так далее. Идея ясна.)
Прошу обратить внимание: сами числа в прогрессии — совершенно любые! Натуральные, целые, дробные, отрицательные, иррациональные — всякие.) А вот их нумерация — всегда строго по порядку! Это важно.
Как же нам записать арифметическую прогрессию в общем виде? Никаких проблем! Каждый член последовательности записывается в виде буквы. Для арифметической прогрессии, обычно, используется буква "а". А вот номер члена всегда указывается индексом справа внизу. Сами члены прогрессии просто перечисляем через запятую или точку с запятой.
Вот так:
а1, а2, а3, а4, а5, а6, …
Здесь а1 — первый член прогрессии, а4 — четвёртый член и т.д. А в конце — многоточие. Всё просто, ничего хитрого.)
Коротко такую прогрессию записывают вот так: (an).
Так обозначаются бесконечные прогрессии. Конечную же прогрессию можно записать просто перечислением всех её членов и точкой в конце.
Например, вот так:
а1, а2, а3, а4, а5, а6.
Или вот так, если членов много:
а1, а2, …, а29, а30.
А вот в краткой записи для конечных прогрессий придётся дополнительно указывать количество членов. Например, вот так:
(an), n=30.
Вот, собственно, и все обозначения.
На этой позитивной ноте считаю наше начальное знакомство с арифметической прогрессией полностью состоявшимся. А теперь, вооружившись глубокими познаниями, можно и задачки порешать. Задачки совсем простые, без фокусов. Чисто для понимания смысла арифметической прогрессии.
Простейшие задания по арифметической прогрессии.
Начнём с такой несложной задачки:
Выпишите первые пять членов арифметической прогрессии (an), если известно, что
а2 = 3 и d = -1,5.
Переводим задание с математического языка на русский. Нам дана бесконечная арифметическая прогрессия. Известен второй член этой прогрессии:
а2 = 3
Кроме того, нам известна разность прогрессии:
d = -1,5
А найти требуется первый, третий, четвёртый и пятый члены этой прогрессии.
Вот и действуем. Для наглядности я сначала запишу последовательность по условию задачки. Прямо в общем виде, где второй член — тройка:
а1, 3, а3, а4, а5, …
А теперь приступаем к поискам. Начинаем, как всегда, с самого простого. Легко можно посчитать, например, третий член a3. Мы же с вами уже знаем (прямо по смыслу арифметической прогрессии), что третий член (а3) больше второго (а2) на величину d.
Так прямо и пишем:
a3 = a2 + d
Подставляем в это выражение тройку вместо a2 и -1,5 вместо d и считаем. Про минус, естественно, тоже не забываем, да.)
a3 = 3 + (-1,5) = 3 — 1,5 = 1,5
Вот так. Третий член оказался меньше второго. Ничего удивительного. Наша разность d — отрицательна. А, если число больше предыдущего на отрицательную величину, то само число, стало быть, будет меньше предыдущего. Убывает наша прогрессия…
Считаем теперь следующий, четвёртый член нашей прогрессии:
a4 = a3 + d
a4 = 1,5 + (-1,5) = 1,5 — 1,5 = 0
Ну и дальше, по проторенной дорожке:
a5 = a4 + d
a5 = 0 + (-1,5) = 0 — 1,5 = -1,5
Отлично, члены с третьего по пятый найдены. Получилась вот такая последовательность:
а1; 3; 1,5; 0; -1,5; …
Осталось лишь найти первый член а1 по известному второму. А это шаг уже в другую сторону — влево.) Это значит, что в данном случае разность d нам надо не прибавить к a2, а отнять.
Получаем:
a1 = a2 — d
a1 = 3 — (-1,5) = 3 + 1,5 = 4,5
Вот и всё.) Ответ к задачке будет такой:
4,5; 3; 1,5; 0; -1,5; …
Что интересного можно заметить в решении данного задания? А заметить можно то, что каждый член прогрессии мы искали по предыдущему (соседнему) члену. Такой способ подсчёта членов прогрессии называется вполне научно — рекуррентным способом. И в дальнейшей работе с прогрессиями (и не только) мы к этому загадочному и страшному слову ещё не раз вернёмся. Так что прошу не пугаться.)
Что ещё важного можно вынести из решения этой, казалось бы, примитивной задачки? А вот что:
Если нам известен хотя бы один член и разность арифметической прогрессии, то мы всегда можем найти любой другой член этой прогрессии. Какой хотим.
Ясненько? Это простое умозаключение позволит вам успешно решать большинство задач школьного курса по данной теме! Все задачи на арифметическую прогрессию вертятся вокруг всего трёх параметров: член прогрессии, разность прогрессии, номер члена прогрессии. И всё!
Разумеется, вся предыдущая математика не отменятся, да.) В солидных заданиях к прогрессии может прицепляться всё что угодно — и уравнения, и неравенства, и прочие жуткие вещи. Но по самой прогрессии всё всегда крутится вокруг этих трёх простых параметров. Так что имеем в виду.)
Следующее задание уже поинтереснее будет, да.)
Определите, будет ли число 6 членом арифметической прогрессии (an), если
a1 = 2,5; d = 1,3.
Гм… И как тут определишь, будет или нет? Кто ж его знает-то… Что делать?
Что-что… Записать прогрессию в виде последовательности чисел и посмотреть, будет ли там шестёрка или нет! Для расчёта нам всё необходимое уже дано: дан первый член, дана разность. Вот и считаем. Прямо по смыслу арифметической прогрессии:
a2 = a1 + d = 2,5 + 1,3 = 3,8
a3 = a2 + d = 3,8 + 1,3 = 5,1
a4 = a3 + d = 5,1 + 1,3 = 6,4
Ну что, стоит считать дальше или нет, как вы думаете? Естественно, нет.) Запишем результаты наших расчётов в виде последовательности:
1,3; 3,8; 5,1; 6,4; …
Теперь уже отчётливо видно, что шестёрку мы просто проскочили мимо между членами 5,1 и 6,4. Не вошла шестёрка в нашу последовательность и, стало быть, число 6 не является членом заданной прогрессии.
Ответ: нет.
А вот теперь задачка на основе реального варианта ОГЭ:
Выписано несколько последовательных членов арифметической прогрессии:
…; 14; х; 8; 5; …
Найдите член прогрессии, обозначенный буквой х.
Что, внушает? Ни первого члена нет, ни разности d, дана просто последовательность чисел без начала и конца. Это и пугает поначалу. А ведь задачка, на самом деле, проще некуда! Чисто на понимание смысла арифметической прогрессии. Кто понимает этот смысл, тот справится с задачкой буквально в уме.
Итак, смотрим внимательно на нашу последовательность и соображаем, что именно можно узнать из неё? Какие параметры арифметической прогрессии из трёх главных в ней спрятаны?
Номера членов? Не-а! Нет здесь ни единого номера. Последовательность у нас простирается как вправо, так и влево…
Да, номеров членов у нас никаких нет, но зато есть четыре числа и (важно!) слово "последовательных" в условии задачи. А лишних слов в условии задачи никогда не бывает… Это слово означает, что наши числа следуют строго по порядку, без пропусков! Теперь смотрим дальше. Есть ли в этой последовательности два соседних известных числа? Да, безусловно! Это 8 и 5. Раз так, то теперь мы без проблем можем найти разность арифметической прогрессии! Берём пятёрку и отнимаем предыдущее число, т.е. восьмёрку.
Получаем:
d = 5 — 8 = -3
Всё. Дальше осталась сущая элементарщина. Какое число будет предыдущим для икса? Четырнадцать! Значит, икс легко ищется простым сложением: к 14 прибавить разность арифметической прогрессии.
Получим:
x = 14 + (-3) = 11
Вот и вся задачка. Ответ: x = 11.
Ещё одна задачка. Уже посолиднее, но тоже довольно простая.
Известно, что в арифметической прогрессии a3 = 2,1 и a6 = 6,3. Найдите a4.
А теперь размышляем. Нас интересует четвёртый член a4. Для его расчёта надо к третьему члену a3 прибавить разность прогрессии d:
a4 = a3 + d
Третий член a3 нам известен. Это 2,1. Отлично! Но… где же взять разность прогрессии? Нет её и в помине! А для её определения нам позарез нужны какие-нибудь два известных соседних члена! Где они? Нет их! Но зато нам зачем-то дан шестой член прогрессии a6. И куда его можно пристроить…
Тупик? Вовсе нет! Сейчас мы с вами поступим по-хитрому. Мы пока ничего считать не будем. Мы будем… рисовать! Да-да! Графическое изображение задачи очень часто высвечивает массу дополнительной информации! И помогает увидеть то, что на словах разглядеть, порой, весьма трудно.
В нашем случае, рисунок поможет нам не только увидеть разность прогрессии d, но и догадаться, как именно следует её искать!
Рисуем задачку!
Берём и схематично изображаем нашу последовательность на числовой оси. Вот так:
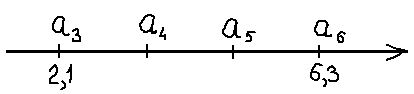
Ну как? Увидели d? Нет? Ну ладно…
А вот так?
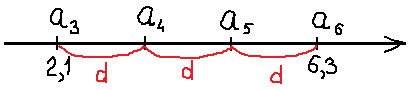
Теперь по картинке чётко видно, что между третьим и шестым членами находится по три равных промежутка. Три раза по d. Или 3d. А какая величина приходится на это самое 3d ? Не проблема! Определим разницу между a6 и a3, да и узнаем:
a6 — a3 = 6,3 — 2,1 = 4,2
3d = 4,2
d = 1,4
Отлично. Полдела сделано. Остались сущие пустяки. Прибавляем найденную разность прогрессии к третьему члену и получаем искомый четвёртый член:
a4 = a3 + d = 2,1 + 1,4 = 3,5
Вот и всё.
Ответ: 3,5
Запоминаем: рисунок к задаче очень часто открывает массу дополнительной полезной информации и подсказывает дальнейший ход решения. Не стесняемся делать его, когда есть возможность!
А вот следующие задачки решаем самостоятельно:
1. Найдите первый отрицательный член арифметической прогрессии, если
a1 = 7 и d = -2,4.
2. Выписано несколько последовательных членов арифметической прогрессии:
…; 3,4; х; 5,2; …
Найдите член прогрессии, обозначенный буквой х.
3. Известно, что число 4 является членом арифметической прогрессии, в которой
a1 = 1 и d = 0,6. Найдите номер этого члена.
4. Известно, что в арифметической прогрессии a2 = 3 и a7 = 23. Найдите a5.
5. Автобус начал движение от остановки, равномерно увеличивая скорость на 2 м/с. Какую скорость разовьёт автобус через 5 секунд? Ответ дайте в км/ч.
6. Известно, что в арифметической прогрессии a2 = -3 и a6 = -15. Найдите a1.
Ответы (в беспорядке, естественно): 15; -0,2; 0; 6; 36; 4,3.
Ну как? Всё получилось? Отлично! Значит, урок не прошёл даром, и можно осваивать арифметическую прогрессию на более серьёзном уровне. В следующих уроках.)
Что-то не получается? Рисуйте картинку, не ленитесь! Она реально спасает в некоторых трудных ситуациях! Если вы видите прогрессию глазами, то решать задачу становится намного легче.
Кстати, в задачке №5 про автобус есть два подводных камня. Первый камень — по правильному составлению арифметической прогрессии. Надо подумать, какую скорость автобуса следует брать за первый член прогрессии. Если вы думаете, что 0 м/с, то задачку не решить, да… А второй подводный камень — по переводу размерностей из одной в другую. Внимательнее читать задание надо, да…
Последняя задача №6 очень похожа на задачу №4. Только числа отрицательные. Ну и что? Рисуем (правильно) картинку и определяем по ней (правильно) величину d. Главное — внимание и элементарное понимание смысла арифметической прогрессии. И всё получится!)
В этом уроке мы с вами познакомились с арифметической прогрессией и её ключевыми параметрами на самом начальном уровне и порешали простенькие задачки. Как видите, ничего сложного. Прибавляй d к числам, считай себе, пиши последовательность или рисуй картинку — всё и решится.
Всё просто, но… Пришло время открыть вам горькую правду. Такое элементарное решение "на пальцах" прокатывает только для очень коротких кусочков прогрессии. Таких, где число последовательно рассчитываемых членов не очень большое. Скажем, три, пять или, пускай, даже десять.
А вот если прогрессия подлиннее, то вычисления значительно усложняются. А рисование картинки — тоже превращается в занятие, мягко говоря, на большого любителя.)
Например, такая задачка:
В арифметической прогрессии известно, что a1 = 4 и d = 0,4. Найдите a141.
И что же, будем много-много раз прибавлять по 0,4? Можно, конечно. Если не жалко часок-другой.)
В таких ситуациях спасает простая формула! По которой такие задания решаются буквально за минуту! Формула эта будет в следующем уроке. И эта злая задачка там будет решена. Тоже за минуту.)
До встречи!
