Теорема Виета в квадратных уравнениях — штука простая и очень-очень важная. Позволяет делать массу полезных вещей буквально в уме. Имеет смысл познакомиться и освоить, правда? Тем более это совсем просто. Сомневаетесь? Напрасно.) Сами увидите. Читаем дальше.
Что такое приведённое квадратное уравнение? Складываем и перемножаем корни…
Знакомство наше начнём с безобидного уравнения:
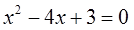
Обычное квадратное уравнение, ничего выдающегося. Коэффициенты a, b и c здесь следующие:
a = 1; b = -4; c = 3
Решаем тоже как обычно, безо всяких фокусов, через дискриминант и получаем два корня:
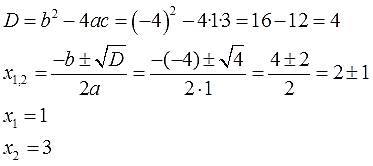
Уравнение как уравнение - и что с того? Ничего, сейчас интересно будет!)
Первым делом я возьму корни нашего уравнения и… сложу их.) Зачем? Так надо!
Итак:
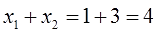
Теперь проделаю ещё одну бесполезную (казалось бы!) штуку. Перемножу корни:
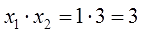
Ну сложил, ну перемножил — и что? Спокойствие и терпение!
Выпишем ещё разок само уравнение, а прямо под ним напишем сумму и произведение корней:
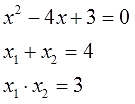
И посмотрим на нашу запись. Внимательно посмотрим… Ничего не бросается в глаза? Ведь многие важные открытия в математике совершались на основе хорошей наблюдательности, между прочим! Не видите…
А вот так?)
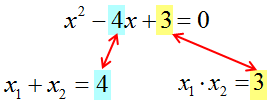
Да! Сумма корней нашего квадратного уравнения равна коэффициенту b. Но, обратите внимание, не просто b, а с противоположным знаком! В уравнении коэффициент при икс (а это и есть буковка b) равен минус четыре. Сумма же корней даёт плюс четыре. То есть, –b.
А произведение корней даёт нам свободный член! Т.е. буковку c. Даёт со своим знаком! Как была в уравнении тройка (с=3), так в произведении корней тройкой же и осталась.)
Теперь я немного изменю уравнение. Поменяю в нём свободный член с тройки на четвёрку. Вот такое уравнение теперь решим:
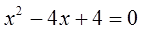
Решаем точно так же, через дискриминант (здесь он равен нулю), и получаем единственное решение x=2.
Но мы с вами люди уже достаточно взрослые и понимаем, что это не один корень, а два одинаковых:
x1,2 = 2
Поэтому снова сосчитаем сумму и произведение корней:
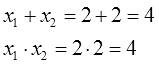
И опять в сумме мы получили –b (-b=+4), а в произведении с (c=+4)!
А вот это уже крайне важно! Оказывается, такая забавная штука будет получаться всегда для любого квадратного уравнения! Если оно имеет корни, разумеется.) Правда, уравнения не какого попало, а такого, где квадрат икса чистый (т.е. коэффициент a=1). В математике такие квадратные уравнения имеют своё особое название — приведённые квадратные уравнения.
Запоминаем:
Квадратное уравнение, в котором коэффициент при х2 равен единице (а=1), называется приведённым квадратным уравнением. Весьма важная штука!
Как оно выглядит в общем виде? Очень просто. Подставим в общий вид квадратного уравнения
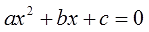
единичку вместо а и получим общий вид приведённого квадратного уравнения:
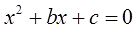
В некоторых учебниках коэффициенты b и с переобозначают другими буквами (чаще всего p и q) и получают вот такой общий вид
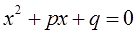
Но суть та же самая. Как говорится, хоть горшком назови… Лично я предпочитаю использовать традиционные буквы b и с. Для универсальности.)
Ну и что из этого? - спросите вы. Чем приведённые квадратные уравнения так выделяются на фоне остальных квадратных, неприведённых? А дело вот в чём.
Что такое теорема Виета?
Итак, мы выяснили, что в приведённом квадратном уравнении (любом!) сумма коэффициентов равна –b, а произведение равно с. Всегда. Ясное дело, если дискриминант неотрицательный и корни у уравнения имеются.
Математически эта фишка записывается вот так:
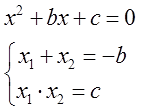
Этот любопытный факт — и есть теорема Виета! Собственной персоной.
А словами она звучит вот как:
Теорема Виета:
Если ПРИВЕДЁННОЕ квадратное уравнение имеет корни, то их сумма равна коэффициенту при икс, взятому с противоположным знаком (-b), а их произведение равно свободному члену (c).
Вот и всё, никаких премудростей.)
Хотите строгое доказательство? Пожалуйста! Флаг вам в руки!) Распишите общую формулу корней квадратного уравнения для a=1, составьте сумму и произведение корней в общем виде. Т.е. через буквы. И упростите. Попробуйте! Весьма полезно и познавательно, между прочим.)
Верна также и обратная теорема:
Если числа х1 и х2 таковы, что их сумма равна –b, а произведение равно c, то эти числа являются корнями приведённого квадратного уравнения x2 + bx + c = 0.
А по секрету скажу вам, что, на самом деле, именно обратной теоремой вы и пользуетесь, так умело подбирая в уме корни уравнения по сумме и произведению! Об этом подборе как раз дальше будет.)
Зачем нужна теорема Виета?
Полезная вещь первая — подбираем корни в уме!
Теорема Виета (обратная форма) позволяет искать корни многих квадратных уравнений гораздо быстрее и проще, чем традиционным путём через дискриминант. В буквальном смысле устно!
Вернёмся к нашему уравнению:
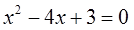
Теперь, вооружившись глубокими познаниями, прямо по теореме Виета, записываем системку для наших искомых корней:
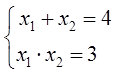
Вопрос на сообразительность: какие же такие два числа в сумме дают четвёрку, а в произведении — тройку? Немного подумав головой, можно довольно быстро догадаться, что это чиселки 1 и 3.
Значит, можно смело записать:
x1 = 1
x2 = 3
Вот и всё. Это и будут корни нашего уравнения. Оба подходят.) Здорово, правда? И не нужно считать никаких дискриминантов, возиться с общей формулой корней. В которой, между прочим, можно и ошибок наляпать… Сразу, в уме, получен верный ответ!
Возможно, кто-то уже приготовил мне вопрос. Очень грамотный вопрос, кстати. А всегда ли в случае приведённого квадратного уравнения можно вот так красиво и легко подобрать корни?
К сожалению, нет. Далеко не всегда. Например, я снова изменю в исходном уравнении свободный член, только вместо четвёрки напишу двойку. Вот такое уравнение пусть будет:
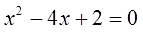
Уравнение приведённое, коэффициент а равен единичке, вроде бы, всё нормально. Пишем теорему Виета:
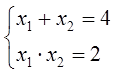
И снова пробуем подобрать иксы так, чтобы оба равенства сработали!
Гм… Что-то не подбирается, правда? Какие бы целые числа вы бы ни подбирали, ничего не выйдет.
Тут выход только один — решать через дискриминант. Ибо дискриминант — штука универсальная. Спасает всегда — и в приведённых уравнениях, и в обычных. Попробуйте. И вы убедитесь, что корни этого уравнения получаются иррациональными. Естественно, такие корни подобрать в уме несколько затруднительно, да…
Догадываюсь, что вы сейчас спросите: Зачем же нам тогда городить огород, пробовать подобрать корни, если дискриминант всё равно надёжнее и с ним-то уж точно всё решится?
Да, надёжнее, но… Не всё так просто, как кажется!
Дело всё в том, что квадратные уравнения изучаются в 8-м классе, где народ тренируется на простых (иногда — совсем примитивных) задачках. И… привыкает к простоте.) Затем, в старших классах и особенно в институте, при изучении высшей математики, квадратные уравнения представляются как нечто само собой разумеющееся. Но при этом в коэффициентах зачастую возникают такие большие числа, что работать с ними большинство учеников… просто не готовы!
Попадётся вам, к примеру, такая задачка:
Из пункта А в пункт В, расстояние между которыми 75 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 82 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт B на 3 часа 25 минут позже автомобилиста. Ответ дайте в км/ч.
Это не моя разыгравшаяся фантазия, а вполне реальная задачка из ЕГЭ, между прочим.)
Кто в курсе, как решать текстовые задачи на движение, тот без труда составит вот такое уравнение:
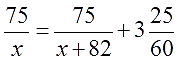
Классическое дробно-рациональное уравнение. Здесь х — скорость велосипедиста. Немного повозившись с ним (избавившись от дробей и упростив всё до упора), получим вот такое квадратное уравнение:
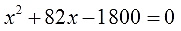
Если начать решать это уравнение по-рабочекрестьянски, то получим, что дискриминант у него равен аж 13924! И… что? Как нам из такого здоровенного числа корень извлекать? Без калькулятора! Слабо? То-то…
Зато через теорему Виета это злое уравнение решается практически устно! Не верите? Что ж, смотрите сами…
Записываем сумму и произведение корней:
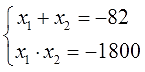
Осталось лишь догадаться, какие же числа дают в сумме минус 82, а в произведении минус 1800. Совсем чуточку подумав, довольно быстро получим, что:
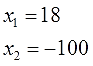
Минус сто, ясное дело, нас не интересует (скорость не бывает отрицательной), а вот 18 км/ч — вполне себе правдоподобная велосипедная скорость.)
Вот и все дела.) И без долгих и утомительных вычислений, связанных с извлечением корня из пятизначного числа! Здорово, правда?
Посему, первые практические советы:
1. Если перед вами квадратное уравнение приведённого вида, то первым делом пробуем найти корни подбором. По теореме, ОБРАТНОЙ теореме Виета. В подавляющем большинстве заданий это срабатывает.
2. Не боимся уравнений с большими коэффициентами! Самое главное — не бросаемся считать дискриминант! Как правило, корни таких уравнений также довольно легко ищутся подбором.
Может, конечно, и не повезти, но зачем же такой шанс упускать, правда?)
Но есть у меня для вас хорошая новость.) Составители большинства заданий — люди гуманные.) И стараются составить уравнение так, чтобы корни являлись целыми числами и их легко можно было бы подобрать. Пробуем делать это!
Переходим к следующей полезной вещи.
Полезная вещь вторая — проверяем корни!
Теорему Виета можно применять не только для подбора корней, но и для проверки корней, найденных другим способом (через дискриминант, например). Решили уравнение - проверьте сумму и произведение корней! Всё срослось — значит, верно. Нет — значит, где-то накосячили. Ищите ошибку.)
Например, такое уравнение:
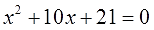
Дело нехитрое. Решаем себе через дискриминант, всё чин-чином, получаем корни:
x1 = -7
x2 = -3
Не бросаемся сразу же радостно писать ответ! Знаете поговорку доверяй, но проверяй?) Вот и не ленимся. Первым делом сложим наши корни:
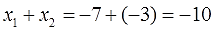
Получили -10. Обратите внимание, не десять, а минус десять! Коэффициент b с противоположным знаком. Так уж теорема Виета устроена.)
Последняя (и окончательная) проверка — перемножим корни. Должен получиться свободный член:
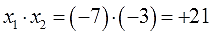
Вот теперь всё хорошо.)
Более того, с этой благородной целью (проверка корней) теорему Виета можно применять и для неприведённых квадратных уравнений. Для любых. Да-да, я не шучу! Но эту фишку я оставлю на конец урока. На десерт.)
И что, думаете, только для подбора и проверки корней теорема Виета и нужна? Вовсе нет!
Полезная вещь третья — когда корни считать… не надо!
Вы спросите, а разве можно обойтись и вовсе без вычисления корней? Можно! Ещё как!)
Дискриминант — штука, безусловно, удобная, простая и понятная. С ним, как правило, всё легко и предсказуемо. Но… Может получиться какой-нибудь дурацкий дискриминант: 17 там, скажем, или 20. Что неизбежно приводит к появлению иррациональных корней, да…) А уж если в задании надо ещё что-то делать с корнями, то выражения с радикалами, даже для опытного ученика, могут перерасти в большую проблему. А для неопытного — вообще превратиться в полный ахтунг.
Но теорема Виета иногда способна на настоящие чудеса!
Например, такое задание:
Дано квадратное уравнение:
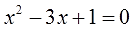
Найдите сумму квадратов корней, не находя самих корней.
Если сейчас начать решать это задание "в лоб" — считать дискриминант и искать корни уравнения по общей формуле, то получим вот таких двух красавцев:
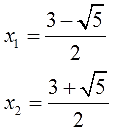
Нам нужна сумма их квадратов. И что нам теперь с такими лохматыми числами делать?! Возводить в квадрат, складывать… Нет, возвести и сложить можно, конечно, но… не каждый ученик дорешает до конца это задание без ошибок!
Не отчаиваемся и читаем ещё раз условие. Обратите внимание, нам вообще НЕ сказано "решать уравнение", НЕ сказано "находить корни". Более того, нам прямым текстом говорится: "Найти сумму квадратов корней, не находя самих корней".
Что делать? Как выкручиваться без поиска корней?
Посмотрим ещё раз на уравнение. Приведённое, между прочим.) Раз так, то, стало быть, для него справедлива теорема Виета!
Можно смело записать:
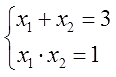
Вот так. Сумма корней — тройка, а произведение — единичка. Мы не знаем, чему равны сами эти корни, но у нас это и не спрашивают. Нас просят найти только сумму их квадратов.)
А вот теперь ключевой вопрос: А можно ли как-то расписать нужную нам сумму квадратов корней через сумму и произведение корней?
Да, можно! Кто на "ты" с формулами сокращённого умножения (а именно — с формулой квадрата суммы), тот, скорее всего, даже не заметит проблем.
Пишем:
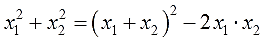
Как я додумался до этого равенства? Очень просто. Вспомнил, что в формуле квадрата суммы сидят сумма квадратов и удвоенное произведение:
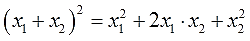
И выразил нужную величину (сумму квадратов) через остальные — сумму (т.е. квадрат суммы) и произведение (удвоенное).
Вот и всё, практически. Осталось лишь подставить тройку вместо суммы и единицу вместо произведения корней, да и посчитать, что получится:
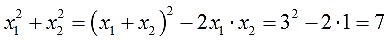
Ответ: 7
И все дела.) И корни не понадобились! Вообще.) Мощная штука — теорема Виета! Ну и формулы сокращённого умножения, само собой.)
Этот приём — выражение какой-то сложной конструкции через сумму и произведение корней — очень популярен в заданиях на теорему Виета! Я уж молчу про более серьёзные задания. Например, задачи с параметрами, там этот финт ушами используется на полную катушку.)
Запоминаем:
В серьёзных заданиях на сумму и произведение корней пользуемся формулами сокращённого умножения и алгеброй 7-го класса! Здорово помогает.)
Как работать с неприведёнными уравнениями?
Как известно, самое сладкое — в конце трапезы. Обещанный десерт.)
Во всех примерах этого урока мы работали лишь с приведёнными квадратными уравнениями. Такими, у которых коэффициент при квадрате икса — единичка. А если уравнение не является приведённым? Т.е. а≠1? Что тогда? Про теорему Виета можно забыть?
Нет, забывать мы не будем. Мы поступим мудро и красиво. Раз уравнение не является приведённым, то мы его… сделаем! Как? Очень просто! Берём квадратное уравнение в общем виде:
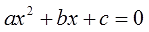
и… делим обе части на "а"! Очищаем квадрат икса от коэффициента. Можно ли так делать? Конечно! Мы ведь с вами уже в курсе, что a никогда не бывает равно нулю (а≠0). Иначе уравнение будет не квадратным, а линейным. Вот и делим смело. Это совершенно безопасно. Естественно, все остальные слагаемые тоже придётся поделить на а, от этого никак не отвертишься.
Получим:
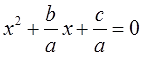
Вот и всё. Уравнение стало приведённым. Коэффициенты, правда, дробными стали, но тут уж ничего не поделать, да…) В этом новом уравнении в роли нового "b" выступает дробь b/a, а в роли нового свободного члена — дробь c/a. Можно записывать теорему Виета:
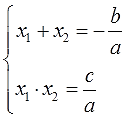
Вот так. Такая модифицированная запись теоремы Виета — более общая. Для любых квадратных уравнений годится — как приведённых (а=1), так и обычных (а≠1). С той лишь разницей, что при а=1 знаменатели исчезают — и теорема обретает свой привычный вид.
Имеет смысл запомнить эту общую форму записи: и для банальной проверки корней пригодится, и, опять же, для более солидных заданий на квадратные уравнения.
Например, надо решить уравнение:
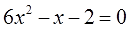
Решаем, получаем корни:
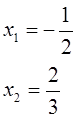
Предположим, вам захотелось проверить, правильно ли вы нашли ваши иксы. Для этого, знамо дело, их надо подставить в исходное уравнение и посчитать результат. Но корни — дробные. Подставлять да считать долго и муторно…
Как проверить корни быстро и с минимумом вычислений? Не проблема! Записываем обобщённую теорему Виета для а=6:
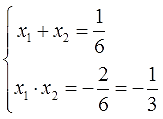
И работаем. Складываем корни:
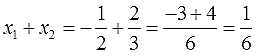
Так, по сумме всё проходит. Осталось перемножить:
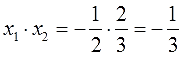
И тут полный порядок! Значит, всё правильно.)
Очередной практический совет:
Найденные корни стараемся проверять! По сумме и произведению. Это здорово уменьшает количество ошибок при решении квадратных уравнений. Если уравнение не является приведённым, то для проверки пользуемся соответствующей модифицированной теоремой Виета.
Итак, мы с вами выяснили, что теорема Виета — штука простая. И очень полезная. И это не только трафаретное решение квадратных уравнений! В ВУЗе, при работе со всякими там пределами, интегралами, дифференциальными уравнениями и прочими прелестями высшей математики, вы ещё не раз вспомните добрым словом знаменитого французского математика с его теоремой.)
Ну что, порешаем?
1. Найдите подбором корни уравнений:
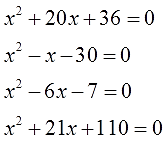
Ответы (в беспорядке):
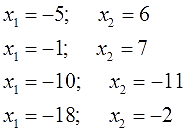
2. Сумма катетов прямоугольного треугольника равна 23 см, а гипотенуза равна 17 см. Найдите больший катет треугольника.
3. Разность корней уравнения 2х2 — 5х + с = 0 равна 1,5. Найдите с.
4. Дано уравнение: x2 — 6x + 4 = 0. Не решая уравнения, найдите сумму кубов его корней.
5. Известно, что х1 и х2 — корни уравнения х2-18х+11 = 0.
Найдите значение выражения:
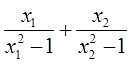
Ответы (в беспорядке):
144; 15; -1; 1
Всё сошлось? Рад за вас! Значит, отныне теорема Виета — не ваша очередная головная боль, а новый надёжный друг и помощник при решении уравнений (и не только квадратных, между прочим!).
Задания 4 и 5 не идут? Корни иррациональные получаются? Это специально.) Да и не нужны они вам… Да, есть там одна загвоздочка. Но алгебра седьмого класса и действия с дробями вам помогут! И этот урок, само собой. И всё получится.)
