Итак, друзья, в прошлом уроке мы познакомились с числовыми и алгебраическими выражениями. Поняли, что означают слова "выражение не имеет смысла". А теперь пришла пора разобраться, что же такое преобразование выражений. И самое главное — зачем оно нужно.
Что такое преобразование выражения?
Ответ прост, до неприличия.) Это любое действие с выражением. И всё. Все эти преобразования вы делали с первого класса. Любое не буквально, конечно… Об этом чуть ниже будет.)
Например, возьмём какое-нибудь суперкрутое числовое выражение Скажем, 3+2. Как его можно преобразовать? Да очень просто! Хотя бы взять да посчитать:
3+2 = 5
Вот этот расчёт детского садика и будет преобразованием выражения. Можно записать то же самое выражение по-другому:
3+2 = 2+3
А тут мы вообще ничего не считали. Просто взяли и переписали наше выражение в другом виде. Это тоже будет преобразованием выражения. Можно записать и по-другому. Например, вот так:
3+2 = 10-5
И эта запись — тоже преобразование выражения.
Или так:
3+2 = 10:2
Тоже преобразование выражения!
Если мы с вами постарше, с алгеброй дружим, то напишем:
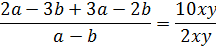
Кто на "ты" с алгеброй, тот, даже особо не напрягаясь и ничего не считая, в уме сообразит, что слева и справа стоит обыкновенная пятёрка. Напрягитесь и попробуйте.)
А если мы совсем уж старшенькие, то можем записать и такие ужастики:
log28+log24 = log232
Или даже такие:
5sin2x+5cos2x=5tgx·ctgx

Внушает? И таких преобразований, очевидно, можно понаделать сколько хочешь! Насколько позволяет фантазия. И набор знаний математики.)
Уловили смысл?
Любое действие над выражением, любая запись его в другом виде называется преобразованием выражения. И все дела. Всё очень просто.
Простота, конечно, дело всегда хорошее и приятное, но за любую простоту где-то надо платить, да…. Есть здесь одно существенное "но". Все эти загадочные превращения всегда подчиняются одному оч-чень важному правилу. Правило это настолько важное, что его смело можно назвать главным правилом всей математики. И нарушение этого простого правила неизбежно будет приводить к ошибкам. Вникаем?)
Предположим, мы преобразовали наше выражение как попало, от балды, как-нибудь вот так:
3+2 = 6+1
Преобразование? Конечно. Мы же записали выражение в другом виде! Но… что здесь не так?
Ответ: всё не так.) Дело всё в том, что преобразования "как попало и от балды" математику не интересуют вообще.) Почему? Потому, что вся математика построена на преобразованиях, в которых меняется внешний вид, но суть выражения не меняется. Таково её жёсткое требование. И нарушение этого требования будет приводить к ошибкам. Три плюс два можно записать в каком угодно виде. В каком пример требует, в том виде и запишем. Но по своей сути это всегда должно быть пять. В каком бы виде мы эти самые 3+2 ни записали. А вот, если, вдруг, после записи выражения 3+2 в другом виде, у вас вместо пяти окажется двадцать пять, где-то вы ошиблись по дороге. Вернитесь да ляп-то и устраните.)
А теперь пришла пора мудрых зелёных мыслей.)
Запоминаем:
1. Любое действие над выражением, запись его в другом виде, называется преобразованием выражения.
2. Преобразования, не меняющие сути выражения, называются тождественными.
3. Вся математика построена на тождественных преобразованиях выражений.
Именно тождественные преобразования и позволяют нам, шаг за шагом, потихоньку-помаленьку, превращать сложный пример в простое, белое и пушистое выражение, сохраняя суть примера. Если, вдруг, в цепочке наших преобразований мы где-то ошибёмся, и на каком-то шаге сделаем НЕ ТОЖДЕСТВЕННОЕ преобразование, то дальше мы будем решать уже совсем другой пример. С другими ответами, да… Которые уже не будут иметь никакого отношения к правильным.) Нарушим тождественность и накосячим ещё где-то - приступим к решению уже третьего примера. И так далее, в зависимости от количества косяков, от задачки про поезд и автомобиль можно прийти к задачке про полтора землекопа.)
Ещё пример. Для школьников, уже вовсю изучающих алгебру. Допустим, нам надо найти значение выражения (40+7)2. Как можно выкрутиться, т.е. преобразовать наше злое выражение? Можно просто посчитать выражение в скобках (получим 47), перемножить столбиком само на себя и получить (если сосчитать) 2209. А можно воспользоваться формулой квадрата суммы
(a+b)2 = a2+2ab+b2.
Получим: (40+7)2 = 402+2∙40∙7+72 = 1600+560+49 = 2209.
Но! Есть соблазн (скажем, в силу незнания формулы) при возведении в квадрат записать просто:
(40+7)2 = 402+72.
К сожалению, на данном простом и, казалось бы, очевидном переходе, тождественность наших преобразований нарушается. Слева всё как надо, 2209, а вот справа — уже другое число. 1649. Посчитайте — и всё станет понятно. Вот вам типичный пример НЕ тождественного преобразования. И соответственно вылезшей ошибки.)
Вот оно и главное правило решения любых заданий: соблюдение тождественности преобразований.
Пример с числовыми выражениями 3+2 и (40+7)2 я привёл чисто для наглядности.
А что же с алгебраическими выражениями? Всё то же самое! Только в алгебраических выражениях тождественные преобразования задаются формулами и правилами. Скажем, в алгебре есть формула:
a(b-c) = ab - ac
Значит, в любом примере мы имеем полное право вместо выражения a(b-c) смело написать альтернативное выражение ab - ac. И наоборот. Это тождественное преобразование. Математика предоставляет нам на выбор эти два выражения. А уж какое из них писать - от конкретного примера зависит.
Или популярное:
a2-b2 = (a-b)(a+b)
Опять же, два возможных варианта. Оба правильные.) Это тоже тождественное преобразование. Что выгоднее писать — разность квадратов или же произведение скобок — пример сам подскажет.)
Ещё пример. Одно из самых главных и нужных преобразований в математике - это основное свойство дроби. Подробнее можно (будет) по ссылочке почитать и посмотреть (когда урок сделаю), а здесь я просто напомню правило:
Если числитель и знаменатель дроби умножить (разделить) на одно и то же число, или неравное нулю выражение, дробь не изменится.
Вот вам пример тождественных преобразований по этому свойству:
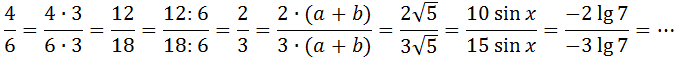
Как вы, наверняка, догадались, эту славную цепочку можно продолжать до бесконечности…) Насколько хватит творческого порыва. Всякие там минусы, корни, синусы, логарифмы пусть вас не смущают. Это всё одна и та же дробь. По своей сути. Две трети. 2/3. Просто записанная в разном виде. :) Очень важное свойство. Именно оно очень часто позволяет превращать всякие монстры-примеры в белые и пушистые.)
Конечно же, формул и правил, задающих тождественные преобразования, - много. Я бы даже сказал, очень много. Но самых главных, без которых в математике хотя бы троечного уровня обойтись нельзя, - вполне разумное количество.
Вот одни из базовых преобразований:
1. Работа с одночленами и многочленами. Приведение подобных слагаемых (или коротко — подобных);
2. Раскрытие скобок и заключение в скобки;
3. Разложение на множители;
4. Формулы сокращённого умножения и разложение квадратного трёхчлена.
5. Работа с дробями и дробными выражениями.
Эти пять базовых преобразований широко используются во всей математике. От элементарной до высшей. И, если вы не владеете хотя бы одной из этих пяти простых вещей, то вас неминуемо ждут большие проблемы как во всей математике средней школы, так и в старших классах, а уж в ВУЗе — тем более. Поэтому именно с них и начнём. В следующих уроках этого раздела.)
Есть и более крутые преобразования. Для продвинутых школьников и студентов.) Будь то:
6. Тригонометрия, логарифмы и всё что с ними связано;
7. Выделение полного квадрата из квадратного трёхчлена;
8. Деление многочленов уголком или по схеме Горнера;
9. Разложение рациональной дроби в сумму элементарных (простейших) дробей. Полезнейшая фишка для студентов при работе с серьёзными интегралами.
Итак, всё ясно насчёт тождественности преобразований и важности её соблюдения? Отлично! Тогда пора двигаться на следующий уровень и шагать из примитивной арифметики в более серьёзную алгебру окончательно. И с блеском в глазах.)
