Приветствую всех, дорогие друзья!
Ну что, поздравляю! Мы с вами благополучно добрались до основного материала в интегрировании рациональных дробей - метода неопределённых коэффициентов. Великого и могучего.) В чём же заключается его величество и могущество? А заключается оно в его универсальности. Имеет смысл ознакомиться, правда? Предупреждаю, что уроков по данной теме будет несколько. Ибо тема очень длинная, а материал крайне важный. )
Сразу скажу, что в сегодняшнем уроке (и последующих тоже) мы будем заниматься не столько интегрированием, сколько… решением систем линейных уравнений! Да-да! Так что те у кого проблемы с системами, повторите матрицы, определители и метод Крамера. А тех товарищей, у кого и с матрицами туго, призываю, на худой конец, освежить в памяти хотя бы "школьные" методы решения систем — метод подстановки и метод почленного сложения/вычитания.
Для начала нашего знакомства отмотаем плёнку немного назад. Ненадолго вернёмся к прошлым урокам и проанализируем все те дроби, которые мы с вами интегрировали до этого. Напрямую, безо всякого метода неопределённых коэффициентов! Вот они, эти дроби. Я рассортировал их по трём группам.
Группа 1

В знаменателе — линейная функция либо сама по себе, либо же в степени. Одним словом, в знаменателе стоит произведение одинаковых скобок вида (х-а).
Например:
(x+4)1 = (x+4)
(x-10)2 = (x-10)(x-10)
(2x+5)3 = (2x+5)(2x+5)(2x+5)
И так далее. Кстати, пусть вас не смущают скобки (4х+5) или (2х+5)3 с коэффициентом k внутри. Это всё равно, по своей сути, скобки вида (х-а). Ибо это самое k из таких скобок всегда можно вынести наружу.
Вот так:
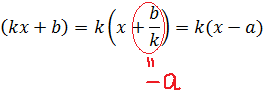
Вот и всё.) И неважно, что именно при этом стоит в числителе — просто dx или же многочлен какой. Мы всегда раскладывали числитель по степеням скобки (x-a), превращали большую дробь в сумму маленьких, подводили (где надо) скобку под дифференциал и интегрировали.
Группа 2
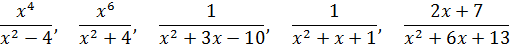
Что общего у этих дробей?
А общее то, что во всех знаменателях стоит квадратный трёхчлен ax2+bx+c. Но не просто, а именно в единственном экземпляре. И неважно здесь, положительный у него дискриминант или отрицательный.
Такие дроби всегда интегрировались одним из двух способов - либо разложением числителя по степеням знаменателя, либо выделением полного квадрата в знаменателе с последующей заменой переменной. Всё зависит от конкретной подынтегральной функции.
Группа 3
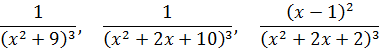
Это были самые нехорошие для интегрирования дроби. В знаменателе — неразложимый квадратный трёхчлен, да ещё и в степени n. Но, опять же, в единственном экземпляре. Ибо, кроме трёхчлена, других множителей в знаменателе нету. Такие дроби интегрировались по рекуррентной формуле. Либо напрямую, либо сводились к ней после выделения полного квадрата в знаменателе и последующей замены переменной.
Однако, к сожалению, всё богатое многообразие рациональных дробей не ограничивается только лишь этими тремя рассмотренными группами.
А как быть, если в знаменателе стоят разные скобки? Например, что-нибудь типа:
(х-1)(х+1)(х+2)
Или одновременно скобка (х-а) и квадратный трёхчлен, что-то типа (х-10)(х2-2х+17)? И в других подобных случаях? Вот, именно в таких случаях и приходит на помощь метод неопределённых коэффициентов!
Сразу скажу: работать мы пока что будем только с правильными дробями. Теми, у которых степень числителя строго меньше степени знаменателя. Как быть с неправильными дробями, подробно рассказано в первом уроке по дробям. Надо выделять целую часть (многочлен). Делением уголком числителя на знаменатель или разложением числителя — как хотите. И даже пример разобран. А многочлен вы уж как-нибудь худо-бедно проинтегрируете. Не маленькие уже поди.) Но на неправильные дроби тоже порешаем примеры!
А теперь начинаем знакомиться. В отличие от большинства учебников по высшей математике, наше знакомство мы начнём не с сухой и грузной теории про основную теорему алгебры, теорему Безу, про разложение рациональной дроби на сумму простейших (об этих дробях позже) и прочего занудства, а начнём мы с несложного примера.
Например, нам требуется найти вот такой неопределённый интеграл:
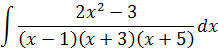
Первый взгляд на подынтегральную дробь. В знаменателе стоит произведение трёх скобок:
(x-1)(x+3)(x+5)
Причём все скобки разные. Поэтому наша старая технология с разложением числителя по степеням знаменателя в этот раз уже не прокатывает: какую именно скобку выделять в числителе? (х-1)? (х+3)? Непонятно… Выделение полного квадрата в знаменателе — тоже не в кассу: там многочлен третьей степени (если перемножить все скобки). Что делать?
При взгляде на нашу дробь возникает вполне естественное желание… Прямо-таки непреодолимое! Из нашей большой дроби, которую неудобно интегрировать, как-то сделать три маленьких. Хотя бы вот так:
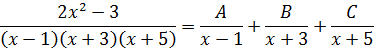
Почему именно такой вид надо искать? А всё потому, что в таком виде наша исходная дробь уже удобна для интегрирования! Подводим знаменатель каждой маленькой дроби под дифференциал и — вперёд.)
А можно ли вообще получить такое разложение? Новость хорошая! Соответствующая теорема математики гласит — да, можно! Такое разложение существует и единственно.
Но есть одна проблемка: коэффициенты А, В и С мы пока не знаем. И сейчас нашей основной задачей как раз и будет их определить. Узнать, чему же равны наши буковки А, В и С. Отсюда и название — метод неопределённых коэффициентов. Начнём наше сказочное путешествие!
Итак, у нас есть равенство, от которого мы начинаем плясать:
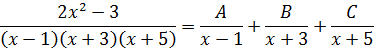
Давайте приведём справа все три дроби к общему знаменателю и сложим:
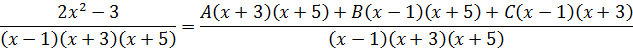
Теперь можно смело отбросить знаменатели (ибо они одинаковы) и просто приравнять числители. Всё как в обычном дробно-рациональном уравнении:
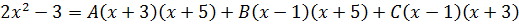
Следующим шагом раскрываем все скобки (коэффициенты А, В и С пока лучше оставить снаружи):
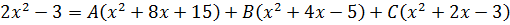
Далее вставляем все коэффициенты внутрь скобок и избавляемся от этих самых скобок:
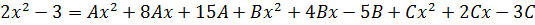
А теперь (важно!) выстраиваем всю нашу конструкцию справа по старшинству степеней: сначала собираем в кучку все члены с х2, потом - просто с иксом и, наконец, собираем свободные члены. Фактически, просто приводим подобные и группируем слагаемые по степеням икс.
Вот так:
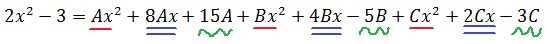
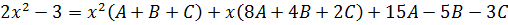
А теперь осмысливаем результат. Слева — наш исходный многочлен. Второй степени. Числитель нашей подынтегральной дроби. Справа — тоже некоторый многочлен второй степени. Но с неизвестными коэффициентами. Данное равенство должно быть справедливо при всех допустимых значениях икс. Дроби-то слева и справа были одинаковые (по нашему условию)! Это означает, что их числители (т.е. наши многочлены) — тоже одинаковые. Стало быть, коэффициенты при одинаковых степенях икс у этих многочленов обязательно должны быть равны!
Начинаем с самой старшей степени. С квадрата. Смотрим, что за коэффициенты у нас стоят при х2 слева и справа. Справа у нас стоит сумма коэффициентов А+В+С, а слева — двойка. Так у нас рождается первое уравнение.
Записываем:
А+В+С = 2
Есть. Первое уравнение готово.)
Далее идём по снижающейся траектории — смотрим на члены с иксом в первой степени. Справа при икс у нас стоит 8А+4В+2С. Хорошо. А что у нас при икс стоит слева? Гм… Слева вообще никакого слагаемого с иксом нету! Там только 2х2 — 3. Как быть? Очень просто! Это значит, что коэффициент при икс слева у нас равен нулю! Мы же можем записать нашу левую часть вот так:
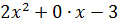
А что? Имеем полное право.) Отсюда второе уравнение выглядит так:
8A+4B+2C = 0
Ну вот, практически, и всё. Осталось приравнять свободные члены:
15А-5В-3С = -3
Одним словом, приравнивание коэффициентов при одинаковых степенях икса происходит по такой схеме:
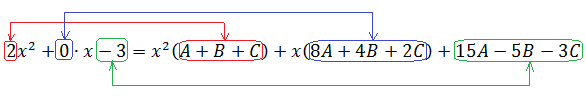
Все три наших равенства должны выполняться одновременно. Поэтому собираем из наших выписанных уравнений систему:
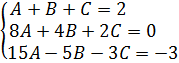
Системка не самая трудная для прилежного студента — три уравнения и три неизвестных. Как хотите, так и решайте. Можно методом Крамера через матрицы с определителями, можно методом Гаусса, можно даже обычной школьной подстановкой.
Для начала я решу эту систему так, как обычно решают такие системы культурные студенты. А именно — методом Крамера.
Решение начинаем с составления матрицы системы. Напоминаю, что эта матрица — просто табличка, составленная из коэффициентов при неизвестных.
Вот она:
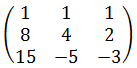
А вот дальше начинаем вычислять определители. Муторно немного, но ничего не поделать. Не школьники уже поди.)
Первым делом вычисляем определитель матрицы системы. Или, коротко, определитель системы. Обычно он обозначается греческой буквой ∆ ("дельта"):
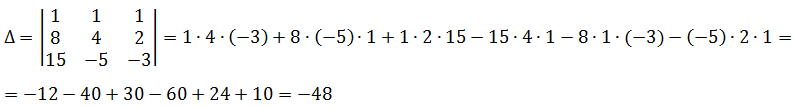
Отлично, определитель системы не равен нулю (-48≠0). Из теории систем линейных уравнений этот факт означает, что наша система совместна и имеет единственное решение.
Следующим шагом вычисляем определители неизвестных ∆A, ∆B, ∆C. Напоминаю, что каждый из этих трёх определителей получается из основного определителя системы путём замены столбцов с коэффициентами при соответствующих неизвестных на столбец свободных членов.
Вот и составляем определители и считаем:
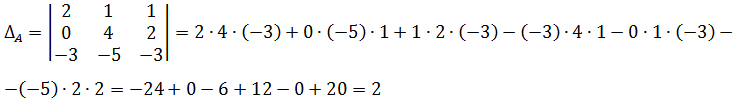
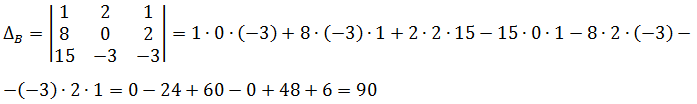
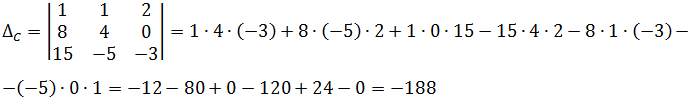
Подробно объяснять технику вычисления определителей третьего порядка я здесь не буду. И не просите. Это уже совсем отклонение от темы будет.) Кто в теме, тот понимает, о чём речь. И, возможно, уже догадался, каким именно способом я вычислил эти три определителя.)
А дальше уже находим неизвестные А, B и С по формулам Крамера:
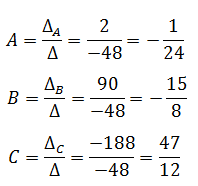
Вот всё и готово.)
Так обычно решают системы культурные студенты. Но… Не все студенты дружат с матрицами и определителями. К сожалению. Для кого-то эти простые понятия высшей математики так навсегда и остаются китайской грамотой и таинственным монстром в тумане…
Что ж, специально для таких некультурных студентов предлагаю более привычный способ решения — метод последовательного исключения неизвестных. Фактически, это продвинутый "школьный" метод подстановки. Только шагов побольше будет.) Но суть та же самая. Первым делом я исключу переменную С. Для этого я выражу С из первого уравнения и подставлю во второе и третье:
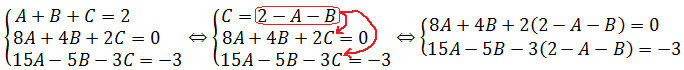
Упрощаем, приводим подобные и получаем новую систему, уже с двумя неизвестными:
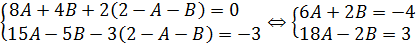
Теперь, в этой новой системе, тоже можно выразить одну из переменных через другую. Но самые внимательные студенты, возможно, заметят, что коэффициенты перед переменной B — противоположны. Два и минус два. Стало быть, очень удобно будет сложить между собой оба уравнения, чтобы исключить переменную В и оставить только букву А.
Складываем левые и правые части, мысленно сокращаем 2B и -2B и решаем уравнение только относительно А:
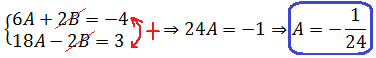
Есть. Первый коэффициент найден: А = -1/24.
Определяем второй коэффициент В. Например, из верхнего уравнения:
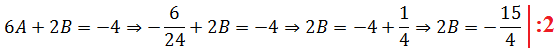
Отсюда получаем:
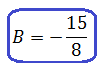
Отлично. Второй коэффициент тоже найден: B = -15/8. Осталась ещё буковка С. Для её определения используем самое верхнее уравнение, где она у нас выражена через А и В:
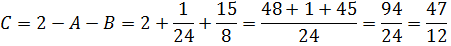
Итак:
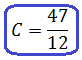
Ну вот и всё. Неизвестные коэффициенты найдены! Неважно, через Крамера или через подстановку. Главное, правильно найдены.)
Стало быть, наше разложение большой дроби в сумму маленьких будет выглядеть вот так:
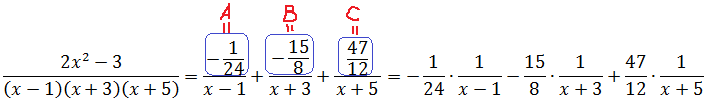
И пусть вас не смущают полученные дробные коэффициенты: в данной процедуре (методе неопределённых коэффициентов) это самое обычное явление. :)
А теперь крайне желательно проверить, правильно ли мы нашли наши коэффициенты A, B и С. Поэтому сейчас берём черновик и вспоминаем восьмой класс — складываем обратно все три наши маленькие дроби.
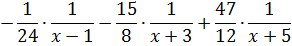
Если мы получим исходную большую дробь — значит, всё хорошо. Нет — значит, бейте меня ищите ошибку.
Общий знаменатель, очевидно, будет 24(х-1)(х+3)(х+5).
Поехали:
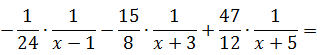
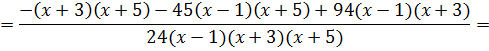
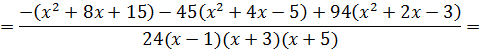
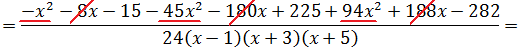
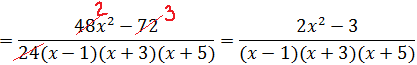
Йес!!! Получили исходную дробь. Что и требовалось проверить. Всё гуд. Так что прошу не бить.)
А теперь возвращаемся к нашему исходному интегралу. Легче он за это время не стал, да. Но теперь, когда наша дробь разложена в сумму маленьких, её интегрирование стало сплошным удовольствием!
Смотрите сами! Вставляем наше разложение в исходный интеграл.
Получаем:
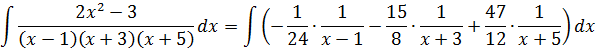
Пользуемся свойствами линейности и разбиваем наш большой интеграл в сумму маленьких, все константы выносим за знаки интеграла.
Получаем:
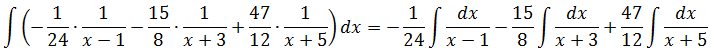
А полученные три маленьких интеграла уже легко берутся подведением знаменателя под знак дифференциала.
Продолжаем интегрирование:
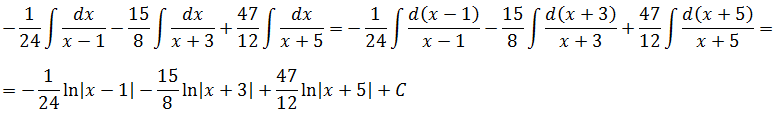
Вот и всё.) И не надо в данном уроке спрашивать меня, откуда в ответе взялись логарифмы! Кто помнит таблицу интегралов, тот в теме и всё поймёт. А кто не помнит — гуляем по ссылочкам. Я их не просто так ставлю.
Окончательный ответ:
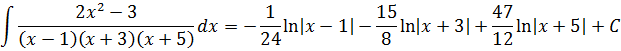
Вот такая красивая троица: три логарифма — трус, бывалый и балбес. :) И попробуй, догадайся до такого хитрого ответа с ходу! Только метод неопределённых коэффициентов и выручает, да.) Собственно, с этой целью и разбираемся. Что, как и откуда.
В качестве тренировочного упражнения, предлагаю вам попрактиковаться в методе и проинтегрировать вот такую дробь:
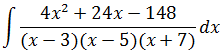
Потренируйтесь, найдите интеграл, не сочтите за труд! Должен получиться вот такой ответ:
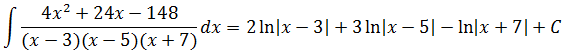
Метод неопределённых коэффициентов — штука мощная. Спасает даже в самой безнадёжной ситуации, когда и так дробь преобразовываешь, и эдак. И вот тут у некоторых внимательных и интересующихся читателей, возможно, возник целый ряд вопросов:
- Что делать, если многочлен в знаменателе вообще не разложен на множители?
- КАК надо искать разложение любой большой рациональной дроби на сумму маленьких? В каком виде? Почему именно в таком, а не сяком?
- Что делать, если в разложении знаменателя есть кратные множители? Или скобки в степенях типа (х-1)2? В каком виде искать разложение?
- Что делать, если, помимо простых скобок вида (х-а), знаменатель одновременно содержит и неразложимый квадратный трёхчлен? Скажем, х2+4х+5 ? В каком виде искать разложение?
Что ж, пришла пора основательно разбираться, откуда ноги растут. В следующих уроках.)
