Итак, продолжаем наше знакомство с основными приёмами интегрирования. В прошлый раз мы научились с вами пользоваться таблицей интегралов и рассмотрели самые простые примеры интегрирования самых простых функций. Теперь настала пора двигаться дальше и понемногу расширять наши возможности.
Итак, метод подведения функции под знак дифференциала — в чём его суть? Вообще говоря, данный метод не является самостоятельным методом интегрирования. Это, скорее, частный случай более общего и мощного метода — метода замены переменной. Или метода подстановки. Почему? А потому, что сам процесс интегрирования подведением под дифференциал всё равно сопровождается последующим введением новой переменной. Звучит пока малопонятно, но на примерах всё куда яснее будет.
Что нам потребуется в сегодняшнем материале:
1) Правило раскрытия дифференциала любой функции f(x). Именно само правило. Строгое определение, что же такое дифференциал, нам здесь не нужно. А правило - вот:
d(f(x)) = f’(x)dx
Всё просто, как в сказке: считаем производную функции f’(x) и помножаем её на dx (дифференциал аргумента).
2) Таблица производных. Да-да! Я серьёзно. :)
3) Таблица интегралов. Ну, логично. Раз уж мы здесь вовсю интегрируем.) Это тема прошлых двух уроков.
4) Правило дифференцирования сложной функции.
Вот, собственно, и всё.Когда чаще всего применяется данный метод? Чаще всего он применяется в двух типовых ситуациях:
Случай 1 — Сложная функция от линейного аргумента
Подынтегральная функция имеет вид:
f(kx+b)
В аргументе — линейная конструкция kx+b. Или, по-другому, под интегралом стоит какая-то сложная функция от линейного аргумента kx+b.
Например:
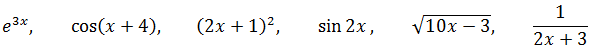
И тому подобные функции. Интегралы от таких функций очень легко сводятся к табличным и берутся в уме буквально через пару-тройку успешно решённых примеров. И мы порешаем.)
Случай 2 — Сложная функция от произвольного аргумента
В данном случае подынтегральная функция представляет собой произведение:
f(g(x))·g’(x)
Иными словами, под интегралом тусуется произведение некой сложной функции f(g(x)) и производной от её внутреннего аргумента g’(x). Или интеграл легко сводится к такому виду. Это более сложный случай. О нём - во второй части урока.
Чтобы не томить народ долгими ожиданиями и разглагольствованиями, сразу приступаем к примерам на случай 1. Будем интегрировать те функции, что я выписал выше. По порядочку.
Как подвести под дифференциал линейную функцию?
И сразу пример в студию.)
Пример 1
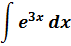
Лезем в таблицу интегралов и находим похожую формулу (это 4-я группа):
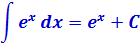
Всё бы хорошо, но… есть проблемка. :) В таблице интегралов в показателе экспоненты ex стоит просто икс. У нас же в показателе тусуется 3х. Три икс. Не катит… Не годится табличная формула для прямого применения: тройка всё испортила. Доцент! А, доцент! Что делать-то будем? (с)
Чтобы справиться с этим примером, нам придётся "подогнать" данный интеграл под табличную формулу. И сейчас я подробно покажу, как именно происходит подгонка. Для этого давайте-ка вернёмся в самое начала раздела и вспомним самую общую запись неопределённого интеграла. В общем виде. Вот она:
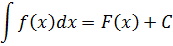
Надеюсь, подробная расшифровка всех значков и буковок в этой записи уже не требуется? Кому всё-таки непонятно, читаем самую первую статью: Что такое первообразная и неопределённый интеграл.
Так вот. Весь фокус состоит в том, что эта самая общая запись неопределённого интеграла будет справедлива не только для переменной икс, но и для любой другой буквы — y, z, t или даже целого сложного выражения. Какого хотим. Важно, чтобы соблюдалось одно единственное требование: в скобочках подынтегральной функции f(…), первообразной функции F(…) и под дифференциалом d(…) стояли одинаковые выражения. Во всех трёх местах! Это важно.
Например:
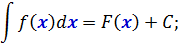
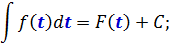
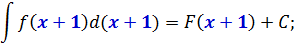
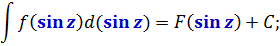
И так далее.) Какая бы буковка и какое бы сложное выражение ни стояли в этих трёх местах, табличная формула интегрирования всё равно сработает! И это неудивительно: любое сложное выражение мы имеем полное право обозначить одной буквой. И работать целиком со всей конструкцией как с одной буквой. А таблице по барабану, какая там буква стоит — икс, игрек, зэт, тэ… Для неё все буквы равноправны.) Поэтому сама конструкция во всех скобочках может при этом быть совершенно любой. Лишь бы одной и той же. )
Поэтому, для нашей конкретной табличной формулы ∫exdx = ex + C, мы можем записать:
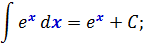
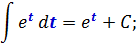
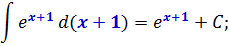
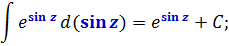
И так далее. Стоять в этих трёх местах может какой угодно монстр. В общем, идея ясна, я надеюсь.)
А теперь порассуждаем. Для того чтобы в нашем примере у нас появилось право воспользоваться таблицей, нам надо добиться того, чтобы под интегралом образовалась вот такая конструкция:
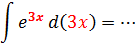
И в показателе и под дифференциалом должно стоять выражение 3х. А теперь посмотрим ещё раз на наш пример:
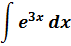
С показателем и так всё как надо, там у нас 3х. По условию.) А вот под дифференциалом пока что стоит просто х. Непорядок! Как же нам из dx сделать d(3x)?
Для достижения этой благородной цели нам надо как-то связать между собой два дифференциала - новый d(3х) и старый dx. В данном случае это очень легко сделать. Если, конечно, знать, как раскрывается дифференциал.)
Получим:
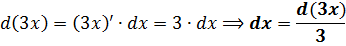
Отлично! Значит, связь между старым и новым дифференциалами будет вот такой:
dx = d(3x)/3.
Что? Не помните, как раскрывать дифференциал? Это вопрос к первому семестру. К дифференциальному исчислению.)
А теперь что делаем? Правильно! Подставляем вместо старого дифференциала dx новое выражение d(3x)/3 в наш пример. Тройка в знаменателе нам уже не помеха: мы её того… наружу. За знак интеграла.)
Что получим:
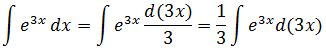
Вот и отлично. В показателе экспоненты и под дифференциалом образовалось совершенно одинаковое выражение 3х. Чего мы, как раз, так усиленно добивались.) И с выражением 3х теперь можно работать целиком, как с одной новой буквой. Пусть t, например. Тогда после замены выражения 3x на t наш интеграл станет выглядеть вот так:
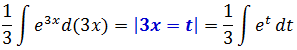
А новый интеграл по переменной t — уже так нужный нам табличный! И теперь можно с чистой совестью воспользоваться табличной формулой и твёрдой рукой записать:
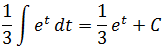
Но расслабляться рано. Это пока ещё не ответ: нам икс нужен, а не t. Осталось лишь вспомнить, что t = 3x и выполнить обратную замену. И теперь наш ответ полностью готов! Вот он:
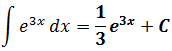
Вот всё и получилось.) Ну что, проверим? А вдруг, напортачили где-то? Дифференцируем результат:
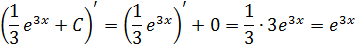
Нет. Всё гуд.)
Пример 2
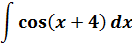
В таблице интегралов функции cos(x+4) нету. Есть просто косинус икс. Но! Если мы как-то организуем выражение х+4 и под дифференциалом d(x+4), то выйдем на табличный интеграл:
∫cos x dx = sin x + C
Итак, связываем наш требуемый новый дифференциал d(x+4) со старым dx:
d(x+4) = (х+4)’·dx = 1·dx = dx
Ух ты, как хорошо! Оказывается, наш новый дифференциал d(x+4) это то же самое, что и просто dx! И безо всяких дополнительных коэффициентов. Халява сплошная!)
Да.) Так и есть. Смело заменяем dx на d(x+4), работаем со скобкой (x+4) как с новой буквой и с чистой совестью пользуемся таблицей.
В этот раз решение запишу чуть компактнее:
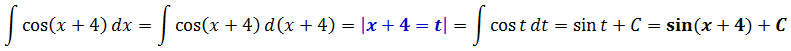
Проверяем результат интегрирования обратным дифференцированием:
(sin(x+4)+C)’ = (sin(x+4))’ + C’ = cos(x+4)∙(x+4)’+0 = cos(x+4)∙1 = cos(x+4)
Всё в шоколаде.)
Ну как, хлопотно? Согласен, хлопотно. Каждый раз выписывать дифференциалы, связывать один с другим, выражать старый дифференциал через новый… Не отчаивайтесь! Есть хорошая новость! Так обычно и не делают. :) Я так подробно расписал решение чисто для понимания сути алгоритма. На практике же поступают гораздо проще. Давайте ещё разок выпишем наши связи между старыми и новыми дифференциалами из обоих примеров:
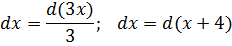
Что можно заметить из этих записей? Два очень важных факта!
Запоминаем:
1) Любой ненулевой числовой коэффициент k (k≠0) можно внести под дифференциал, для компенсации разделив полученный результат на этот коэффициент:
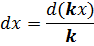
2) Любое постоянное слагаемое b можно внести под дифференциал без последствий:
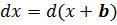
Строго доказывать данные факты не буду. Ибо просто это. Из примеров и так всё понятно, надеюсь.) Если хотите строгости — ради бога. Упрощайте правые части обоих равенств, раскрывая дифференциалы. И там и там получите просто dx. :)
Данные два факта можно легко объединить в один, более универсальный.
Любую линейную конструкцию kx+b можно внести под дифференциал dx по правилу:
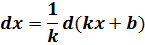
Подобная процедура носит название подведение функции под знак дифференциала. В данном случае под дифференциал подводится линейная конструкция kx+b. Мы искусственно превращаем неудобный нам дифференциал dx в удобный d(kx+b).
И зачем нам такие ужасающие возможности — спросите вы? Просто так — незачем. Но зато с помощью такого искусного манёвра очень многие нетабличные интегралы теперь будут щёлкаться буквально в уме. Как орешки.)
Смотрите!
Пример 3
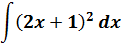
Этот пример будем сводить к табличному интегралу от степенной функции:
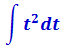
Для этого подведём под дифференциал нашу линейную конструкцию 2х+1, стоящую под квадратом. То есть, вместо dx пишем d(2x+1). Так нам надо. Но математике надо, чтобы от наших действий суть примера не изменилась! Поэтому идём на компромисс и, согласно нашему правилу, домножаем дополнительно всю конструкцию на коэффициент 1/2 (у нас k = 2, поэтому 1/k = 1/2).
Вот так:
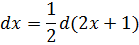
И теперь считаем:
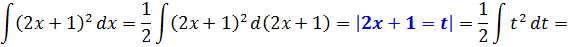
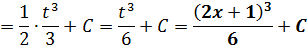
Готово дело.) А вот тут у некоторых читателей может возникнуть вопрос. Очень хороший вопрос, между прочим!
Мы ведь могли и не подводить выражение 2х+1 под дифференциал, не вводить никакую новую переменную, а просто взять и тупо возвести скобки в квадрат по школьной формуле квадрата суммы
(2х+1)2 = 4х2+4х+1,
после чего почленно (в уме!) проинтегрировать каждое слагаемое. Можно так делать? Конечно! А почему — нет? Попробуйте! И сравните полученные результаты. Будет вам там сюрприз! Подробности — в конце урока. :)
А мы пока движемся дальше. Оставшиеся примеры распишу уже без особых комментариев… Подводим линейный аргумент kx+b под дифференциал, а образовавшийся коэффициент 1/k выносим за знак интеграла. И срабатываем по таблице. Окончательные ответы выделены жирным шрифтом.
Пример 4
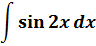
Легко!
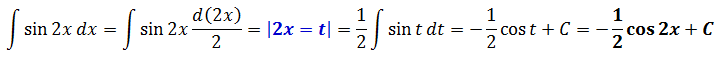
Пример 5
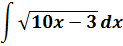
Без проблем!
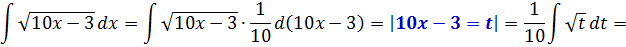
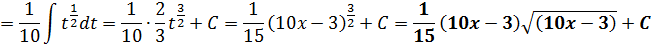
И, наконец, последний пример.
Пример 6
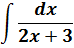
И тут всё проще простого!
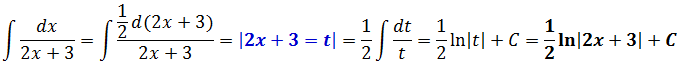
Ну как? Понравилось? И теперь такие примеры вы можете щёлкать в уме! Заманчивая возможность, правда?) Более того, сами подобные интегралы частенько бывают отдельными слагаемыми в более накрученных примерах.
Кстати сказать, после определённого навыка работы с таблицей первообразных, со временем полностью отпадает необходимость вводить новую промежуточную переменную t. За ненадобностью.
Например, очень скоро, вы сразу в уме на подобные примеры будете давать готовый ответ:
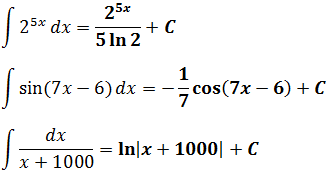
И так далее…
И даже в один присест расправляться с монстрами типа:
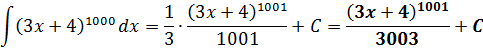
А вы попробуйте вычислить данный интеграл "в лоб", через возведение в 1000-ю степень по формуле бинома Ньютона! Придётся почленно интегрировать 1001 слагаемое, да… А вот с помощью подведения под дифференциал — в одну строчку!
Так, ну хорошо! С линейной функцией всё предельно ясно. Как именно подводить её под дифференциал — тоже. И тут я слышу закономерный вопрос: а только ли линейную функцию можно подвести под дифференциал?
Разумеется, нет! Любую функцию f(x) можно подвести под дифференциал! Ту, которая удобна в конкретном примере. А уж какая там удобна — от конкретного примера зависит, да… Просто на примере линейной функции очень просто демонстрировать саму процедуру подведения. На пальцах, что называется.) А теперь мы плавненько подходим к более общему случаю 2.
Как подвести под дифференциал любую произвольную функцию?
Речь пойдёт о случае, когда подынтегральная функция имеет вот такой вид:
f(g(x))·g’(x).
Или, что то же самое, подынтегральное выражение имеет вид:
f(g(x))·g’(x)dx
Ничего особенного. Просто dx приписал.)
Одним словом, речь пойдёт об интегралах вида:
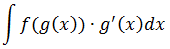
Не пугаемся всяких штрихов и скобочек! Сейчас всё куда яснее станет.)
В чём здесь суть. Из исходной подынтегральной функции можно выделить сложный аргумент g(x) и его производную g’(x). Но не просто выделить, а расписать именно в виде произведения некой сложной функции f(g(x)) от этого самого аргумента на его производную g’(x). Что и выражается записью:
f(g(x))·g’(x)
Перефразируем теперь всё в терминах дифференциала: подынтегральное выражение можно представить в виде произведения некой сложной функции f(g(x)) и дифференциала её аргумента g’(x)dx.
Разбираемся дальше. Мы с вами знаем (надеюсь), что g’(x)dx = d(g(x)). Прямо по смыслу дифференциала.)
И тогда, стало быть, всё наше подынтегральное выражение можно расписать вот так:
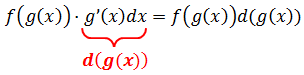
Говоря по-русски, мы вносим промежуточную функцию g(x) под знак дифференциала. Было dx, а стало d(g(x)). И зачем нам эти метаморфозы? А затем, что, если сейчас ввести новую переменную t = g(x), то наш интеграл существенно упростится:
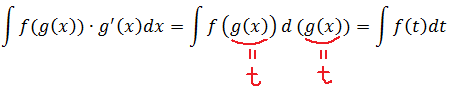
И, если новый интеграл по новой переменной t вдруг (!) окажется табличным, то всё в шоколаде. Празднуем победу! )
"Многа букафф", да. Но на примерах сейчас всё куда понятнее будет. :) Итак, вторая часть пьесы!
Пример 7
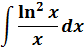
Это классика жанра. Под интегралом дробь. Напрямую таблицей не воспользуешься, никакими школьными формулами ничего не преобразуешь. Только подведение под дифференциал и спасает, да.) Для этого распишем нашу подынтегральную дробь в виде произведения. Хотя бы вот такого:
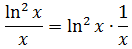
А теперь разбираемся. С логарифмом в квадрате всё ясно. Он и в Африке логарифм… А что такое 1/x? Вспоминаем нашу незабвенную таблицу производных… Да! Это производная логарифма!
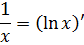
Вставляем теперь в подынтегральную функцию вместо 1/х выражение (ln x)’:
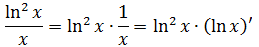
Вот мы и представили исходную подынтегральную функцию в нужном нам виде f(g(x))·g’(x). Превратили её в произведение некой функции от логарифма f(ln x) и производной от этого самого логарифма (ln x)’. А именно — в произведение ln2x и (ln x)’.
А теперь давайте подробно расшифруем, какие же именно действия у нас скрываются за каждой буковкой.
Ну, с функцией g(x) всё ясно. Это логарифм: g(x) = ln x.
А что же скрывается под буквой f? Не всех осеняет сразу… А под буквой f у нас скрывается действие - возведение в квадрат:
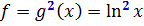
Вот и вся расшифровка.)
А всё подынтегральное выражение можно теперь переписать вот так:
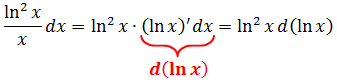
И какую же функцию мы внесли под дифференциал в данном примере? В данном примере мы внесли под дифференциал логарифмическую функцию ln x!
А дальше всё очевидно. Заменяем теперь наш логарифм новой буквой t, вставляем в пример и получаем вместо ужасной дроби безобидный табличный интеграл от… степенной функции! :)
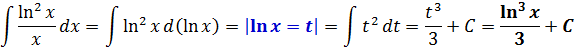
Готово дело.) Для того чтобы убедиться в правильности результата, всегда можно (и нужно) продифференцировать ответ:
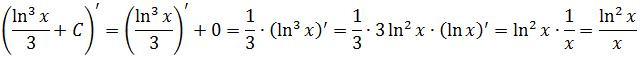
Ура! Всё ОК.)
А теперь обратите внимание, как именно мы дифференцируем окончательный ответ всех примеров этого урока. Неужели до сих пор не уловили закономерность? Да! Как сложную функцию! Оно и естественно: дифференцирование сложной функции и подведение функции под знак дифференциала — это два взаимно обратных действия. :)
Это был довольно несложный пример. Чтобы разобраться, что к чему. Теперь пример посолиднее.)
Пример 8
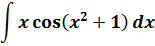
Опять же, впрямую ничего не решается. Попробуем метод подведения под дифференциал с последующей заменой. Вопрос — что подводить и заменять будем? А вот тут уже задачка.)
Нам надо попробовать подынтегральную функцию x·cos(x2+1) как-то представить в виде произведения функции от чего-то на производную этого самого чего-то:
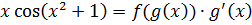
Ну, произведение у нас и так уже есть — икса и косинуса.) Чутьё подсказывает, что функцией g(x), которую мы и будем подводить под дифференциал, будет выражение x2+1, которое сидит внутри косинуса. Прямо таки напрашивается:
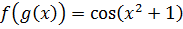
Всё чётко. Внутренняя функция g — это x2+1, а внешняя f — это косинус.
Хорошо. А теперь давайте проверим, не связан ли как-то оставшийся множитель x с производной выражения x2+1, которое мы выбрали в качестве кандидата на подведение под венец дифференциал.
Дифференцируем:
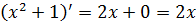
Да! Связь налицо! Если 2x = (x2+1)’, то для одинарного икса мы можем записать:
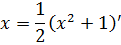
Или, в виде дифференциалов:
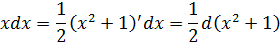
Всё. Кроме x2+1, никаких других выражений с иксом у нас больше нигде в примере нет. Ни в подынтегральной функции, ни под знаком дифференциала. Чего мы и добивались.
Переписываем теперь наш пример с учётом этого факта, заменяем выражение x2+1 новой буквой и — вперёд! Правда, это… Коэффициент 1/2 ещё вылез… Не беда, мы его наружу, наружу! :)
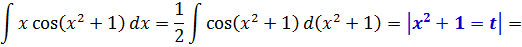
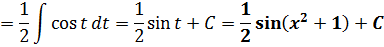
Вот и всё. Как мы видим, в предыдущем примере под дифференциал вносилась логарифмическая функция, а здесь — квадратичная.
Рассмотрим теперь более экзотический пример.
Пример 9
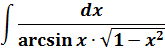
На вид ужас-ужас! Однако, горевать рано. Самое время вспомнить нашу горячо любимую таблицу производных.) А чуть конкретнее — производную арксинуса.
Вот она:
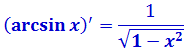
Тогда, если подвести этот самый арксинус под дифференциал, то этот злой пример решается в одну строчку:
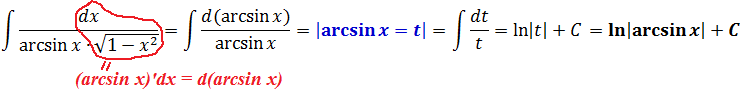
И все дела!
А теперь, давайте на данном примере проанализируем весь наш увлекательный процесс подведения функции арксинус под дифференциал. Что нам пришлось сделать, чтобы успешно справиться с этой задачей? Нам пришлось опознать в выражении
производную другого выражения — арксинуса! Иными словами, сначала вспомнить (по таблице производных), что
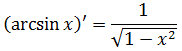
и затем сработать справа налево. Вот так:
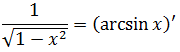
А вот это уже посложнее, чем простое дифференцирование, согласитесь! Точно так же, как и, например, извлекать квадратный корень сложнее, чем возводить в квадрат.) Нам приходится подбирать нужную функцию. По таблице производных.
Поэтому, помимо прямого дифференцирования, в интегрировании нам ещё надо будет постоянно проводить обратную операцию - распознавать в функциях производные других функций. Здесь чёткого алгоритма нет. Тут практика рулит.) Рецепт здесь один — решать примеры! Как можно больше. Прорешаете хотя бы 20-30 примеров — и такие замены вы будете замечать и проделывать достаточно быстро и легко. На автомате, я бы даже сказал. И обязательно надо знать таблицу производных! Наизусть.)
Я даже не поленюсь и самые популярные конструкции сведу в отдельную таблицу дифференциалов.
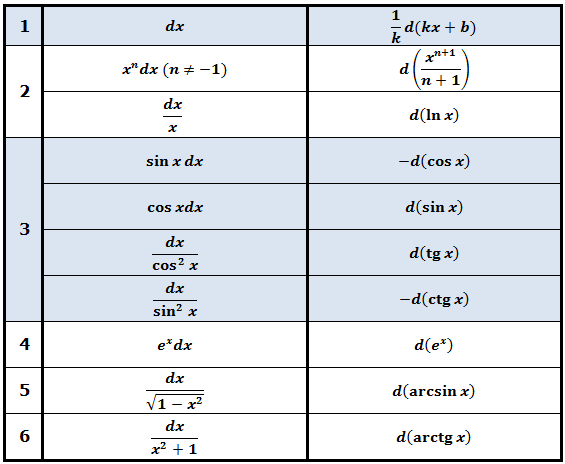
Этой небольшой сводной таблички уже вполне достаточно, чтобы успешно расправляться с большей частью примеров, решаемых методом подведения функции под знак дифференциала! Имеет смысл разобраться. :)
Скажу отдельно, что конструкция dx/x и соответствующий ей табличный интеграл ln|x| — одни из самых популярных в интегрировании!
К этой табличной формуле с логарифмом сводятся все интегралы от дробей, числитель которых является производной знаменателя. Смотрите сами:
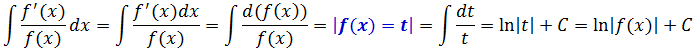
Например, даже безо всякой замены, по этому правилу можно в одну строчку проинтегрировать тангенс, к примеру. Кто-то тут как-то спрашивал про тангенс? Пожалуйста!
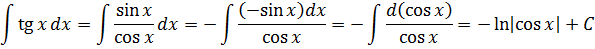
И даже такие гиганты тоже интегрируются в одну строчку!
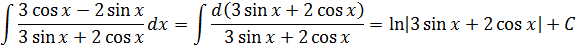
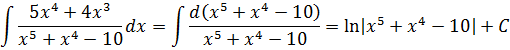
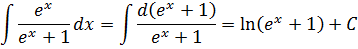
Забавно, правда? :)
Возможно, у особо глазастых возник вопрос, почему в первых трёх случаях я под логарифмом написал модуль, а в последнем случае — не написал?
Ответ: выражение ex+1, стоящее под логарифмом в последнем примере, положительно при любом действительном x. Поэтому логарифм от выражения ex+1 всегда определён, и в данном случае вместо модуля можно использовать обычные скобки. :)
А зачем вообще под логарифмом в табличном интеграле стоит модуль? Ведь, в таблице производных у логарифма никакого модуля нету и при дифференцировании мы спокойненько пишем:
(ln x)’ = 1/х
А при интегрировании функции 1/x ещё и модуль зачем-то пишем…
На этот вопрос отвечу позже. В уроках, посвящённых определённому интегралу. Связан этот модуль с областью определения первообразной.
Заметьте: мы, как фокусники в цирке, по правде говоря, просто осуществляем какой-то набор махинаций с функциями, превращая их друг в друга по некой табличке. :) А с областью определения пока что вообще никак не паримся. И, по правде говоря, зря. Ведь мы работаем всё-таки с функциями! А область определения — важнейшая часть любой функции, между прочим! :) В том числе и тех функций, с которыми мы здесь работаем — подынтегральной f(x) и первообразной F(x). Так что про область определения мы ещё вспомним. В специальном уроке.) Терпение, друзья!
Вот мы и рассмотрели с вами типовые примеры интегралов, решаемых подведением функции под знак дифференциала.) Сложно? Поначалу — да. Но после определённой тренировки и выработки навыка такие интегралы вам будут казаться одними из самых простых!
А теперь — обещанный сюрприз! :)
Давайте вновь вернёмся к примеру №3. Там, подводя выражение 2х+1 под дифференциал, мы получили вот такой ответ:
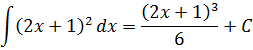
Это правильный ответ. Продифференцируйте на бумажке, как сложную функцию, и убедитесь сами. :)
А теперь рассмотрим другой способ решения этого же примера. Не будем ничего подводить под дифференциал, а просто тупо раскроем квадрат суммы и почленно проинтегрируем каждое слагаемое. Имеем полное право!
Получим:
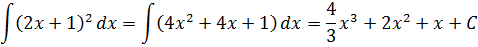
И это тоже правильный ответ!
Вопрос: первый и второй ответы к одному и тому же интегралу – одинаковы или различны?
Ведь, по логике, ответы к одному и тому же примеру, полученные двумя разными способами, должны совпадать, не так ли? Сейчас узнаем! Преобразуем первый результат, раскрыв куб суммы по формуле сокращённого умножения (a+b)3 = a3+3a2b+3ab2+b3.
Что получим:
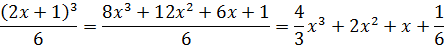
А теперь сравниваем оба результата:
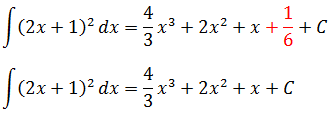
И… что-то тут не так! Откуда же в первом результате взялась "лишняя" дробь 1/6? Получается, что к одному и тому же интегралу получены два разных ответа!
Парадокс? Мистика?
Спокойствие! Разгадка тайны кроется в определении неопределённого интеграла. Вспоминаем самый первый урок по интегрированию. :) Там зачем-то приведена оч-чень важная фраза: две первообразные одной и той же функции F1(x) и F2(x) отличаются друг от друга на константу.
А теперь вновь всматриваемся в наши результаты. И… видим, что в нашем случае так и есть: полученные двумя разными путями ответы как раз и отличаются на константу. На одну шестую. :)
F1(x) — F2(x) = 1/6
Вот и весь секрет. Так что никакого противоречия нет. :)
Дальше — больше! Посмотрим теперь на интеграл из примера №4:
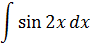
А его вообще можно взять аж… тремя различными способами! Не верите? Смотрите cами! :)
Способ №1. Синус двойного угла не трогаем, а просто подводим аргумент 2x под дифференциал (как, собственно, уже делали в процессе разбора):
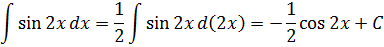
Способ №2. Раскрываем синус двойного угла, под дифференциал подводим sin x:
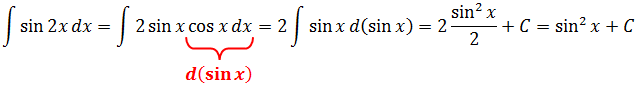
Способ №3. Снова раскрываем синус двойного угла, но под дифференциал подводим cos x:
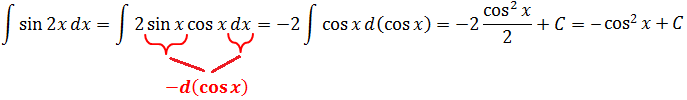
А теперь дифференцируем все три ответа и удивляемся дальше:
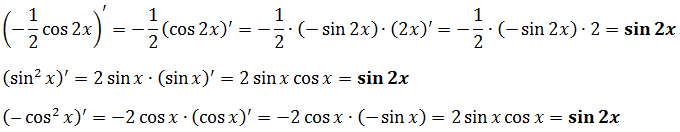
Чудеса, да и только! Получилось три разных ответа! Причём в этот раз даже внешне не похожих друг на друга. А производная — одна и та же! :) Неужели дело опять в интегральной константе, и каждая из трёх функций отличается от другой на константу? Да! Как это ни странно, но это именно так.) А вы поисследуйте эти три функции самостоятельно! Не сочтите за труд. :) Преобразуйте каждую функцию к одному виду - либо к sin2x, либо к cos2x. И да помогут вам школьные формулы тригонометрии! :)
К чему я рассмотрел эти сюрпризы и вообще затеял все эти светские беседы про интегральную константу?
А дело вот в чём. Как вы видите, даже небольшое различие в интегральной константе способно, в принципе, сильно изменить внешний вид ответа, да… Но фишка в том, что от этого ответ не перестаёт быть правильным! И, если в сборнике задач вы, вдруг, увидите ответ, не совпадающий с вашим, то огорчаться рано. Ибо этот факт вовсе не означает, что ваш ответ неверен! Возможно, что вы просто пришли к ответу иным путём, чем предполагал автор примера. Так бывает.) А убедиться в правильности ответа всегда поможет самая надёжная проверка, основанная на определении неопределённого интеграла. Какая? Правильно! Дифференцирование окончательного ответа! Получили подынтегральную функцию — значит, всё ОК.
Ну как, прочувствовали теперь, насколько важен значок dx под интегралом? Во многих примерах только он и спасает, да. Мощная штука! Так что теперь не пренебрегаем им! :)
А теперь — тренируемся! Поскольку тема не самая простая, то и примеров для тренировки в этот раз будет больше обычного.
Методом подведения функции под знак дифференциала найти неопределённые интегралы:

Ответов в этот раз давать не буду. Так будет неинтересно. :) Не ленитесь дифференцировать результат! Получили подынтегральную функцию — ОК. Нет — ищите, где накосячили. Все примеры очень простые и решаются в одну (максимум две) строчки. Кому позарез нужны ответы, все примеры взяты из сборника задач по матанализу Г.Н. Бермана. Скачивайте, ищите свой пример, сверяйтесь. :) Успехов!
