Ну что, дорогие товарищи! Могу вас поздравить! Мы с вами медленно, но верно взрослеем! И математика, с которой мы с вами будем работать, тоже потихоньку будет становиться серьёзнее, да.)
В чём же будет заключаться наше взросление? А взросление будет заключаться вот в чём.
Все мы с начальной школы уже попривыкли работать с числами. Складывать/вычитать, умножать/делить числа. Самые разные — целые и дробные, положительные и отрицательные.... Но! Жизнь — штука многогранная! И преподносит много сюрпризов. И вот один из них.
В жизни очень часто приходится работать с различными числовыми величинами не в конкретном, а в общем виде. Это может быть время, расстояние, температура, цена, скорость — совершенно любая числовая величина. Т.е. величина, которую как-то можно выразить числом (секунд, дециметров, рублей, километров в час и так далее). Взаимоотношения между величинами задаются в математике, чаще всего, формулами. Прямо в общем виде. Или уравнениями. Вспомните хотя бы простенькие задачки на движение, для решения которых используется ключевая формула:
S = V·t
S — пройденный путь,
V — скорость движения,
t — время движения.
К сожалению, для работы с числовыми величинами в общем виде, одних только чисел (т.е. набора циферок) уже недостаточно. Требуются ещё и буквы. Которые как раз и характеризуют нужную нам величину в общем виде. Стало быть, для работы с общей (буквенной) записью числовых величин (т.е. формулами и уравнениями) нужна своя математика. И она есть! Как только к чиселкам в употребление добавляются ещё и буковки, то привычная нам арифметика превращается в… Превращается в… грамматику?) Не-а! Не угадали.) В алгебру! Красивое и мощное слово.)
Естественно, в новом разделе математики (алгебре) возникают свои правила и свои порядки. Некоторые вещи будут хорошо знакомы вам из арифметики (сложение/вычитание, умножение/деление, сокращение дробей, возведение в степень и т.д.), но некоторые будут и непривычными. Почему? А потому, что новыми! А любая новизна всегда предполагает некоторый период привыкания, да.) Вот и мы освоимся и попривыкнем.
Что изучает алгебра? Как работает алгебра?
Итак, предмет алгебры. Что же изучает алгебра?
Фактически, алгебра — это просто обобщение изучения арифметики. Ни больше, ни меньше.
То есть, алгебра - это изучение всё тех же чисел и работы с ними. Только более общее.) Всё отличие будет состоять лишь в том, что, помимо уже привычных нам чисел и числовых выражений, в игру дополнительно вступают буквы и соответственно буквенные выражения. Но, сразу прошу заметить, не просто буквы в буквальном смысле, как буквы в русском языке или литературе.
Итак, удивляемся, но запоминаем. Буквы в алгебре — это, фактически, те же самые числа! Только числа эти замаскированные. Или подразумевающиеся. И поэтому носят особое название — переменные величины. Или кратко — переменные.
Почему — переменные? А потому, что под любой буквой в алгебре всегда скрывается какое-то число. И любую букву при желании можно заменять на какое-то число. Совершенно любое (какое допустимо, конечно). Об этом в первом уроке про числовые и алгебраические выражения немного говорилось. Но и тут не грех вспомнить будет.)
Например, возьмём конкретное алгебраическое выражение. Пусть а+1. В нём есть единичка (число 1), которая вопросов обычно ни у кого не вызывает. Единичка и в Африке единичка. И ещё есть буковка "а". А вот тут уже у многих появляются вопросы, да… Что это за буква такая? Что она означает и зачем вообще написана?
Ответ: буковка "а" – это и есть та самая переменная величина.
Обратите внимание! Несмотря на свой переменный характер, величина эта — тоже числовая. Хоть и обозначена буковкой (казалось бы!). Потому что под этой буковкой мы можем подразумевать совершенно любое число. Какое угодно. Хоть 5, хоть -34, хоть 1,87, хоть 0 — любое число. Целое, дробное, отрицательное — какое хотим. Но — именно число. Уловили?
Между прочим, простенькие алгебраические выражения очень легко и просто расшифровываются словесно. Да-да! Великий и могучий русский язык способен очень на многое. В том числе и в математике, да.
Например, словесная расшифровка нашего злого выражения а+1 будет при этом гласить: к любому числу (а) прибавить единичку (1).
Обратите внимание на слова — именно "любому числу" (а не букве!). Не можем мы складывать буквы с числами "в лоб". Как и не можем складывать метры с килограммами, да…
Запоминаем:
Буквы в алгебре — это просто символы! Под которыми скрываются различные числа. И не более того. Буквы можно заменять на различные числа.
Конечно, под буквами и не только числа могут скрываться. Могут и целые выражения, и синусы, и логарифмы, и даже функции могут скрываться, - всё что угодно: алгебра не только с числами работает! Но об этих фокусах позже. Всему своё время.)
Потренируемся теперь в словесной расшифровке более сложных алгебраических выражений. Возьмём другое выражение. Посложнее. Например:
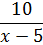
Так прямо по-русски и читаем: десятку (10) поделить на разность любого числа (х) и пятёрки (5).
Конечно, здесь число икс может быть уже не совсем любым. Про смысл алгебраического выражения помните? И чем же у нас не может быть икс в этом выражении? Правильно, пятёркой не может быть! То есть, числом, при подстановке которого получается запретное действие (в данном случае — деление на ноль).
А как словесно расшифровать выражение, скажем, x+y?
Легко! К любому числу икс (х) прибавить любое число игрек (у).
Или так: сумма любых двух чисел икс (х) и игрек (у).
Да-да! Именно так. Только весь фокус этого алгебраического выражения состоит в том, что под буквами икс и игрек скрываются (подразумеваются), в общем случае, уже разные числа. Именно поэтому используются и разные буквы, да.)
Например, если бы мы твёрдо были уверены, что нам надо сложить два одинаковых числа (например, 1+1 или 5+5), то алгебраически мы бы записали:
х+х или а+а.
А вот если нам надо сложить два разных числа (скажем, 1+2 или 5+7) то для этого другого числа нам и букву другую выбирать приходится, да… Такова суровая жизнь.)
Запоминаем:
В алгебре под одинаковыми буквами подразумеваются одинаковые числа. А под разными буквами — в общем случае, разные числа.
Почему я сделал оговорку "в общем случае"? Потому, что в частном случае — да, под разными буквами могут оказаться и одинаковые числа. При желании.) Скажем, в выражении х+у мы же имеем право взять икс и игрек по единичке? Имеем! Сложим — получится двойка. Возьмём икс и игрек по сотке и сложим — получим двести. И так далее…
Но любой частный случай — лишь часть общего. На то он и частный, да.) А в общем случае, данная запись говорит нам о том, что числа икс и игрек — разные. И буквы — тоже разные.
Понимание сути назначения чисел и букв в алгебре позволяет, как минимум, понимать и решать простейшие задания. Например, такое:
Найдите значение выражение 2b+3 при b = 0,3.
Всё проще простого. Если не понимать смысл назначения буковки b в выражении 2b+3, задание не решить, да… Но мы-то ведь уже в теме, правда?)
Итак, мы знаем, что в алгебраическом выражении 2b+3 под буквой b (или переменной b, что одно и то же) скрывается какое-то число. Какое именно — обычно мы не знаем. Но в нашем задании значение b указано конкретно прямым текстом. Это 0,3. Что надо сделать? Правильно, просто тупо подставить вместо b число 0,3 да и посчитать, что получится:
2·0,3+3 = 0,6+3 = 3,6
Это правильный ответ.
Если бы в задании было бы сказано: "… при b = 0", что бы мы делали? Правильно! Подставляли бы вместо b нолик. И снова считали. Получили бы 3. И так далее. Улавливаете?)
Или другое задание. Покруче.
Имеет ли смысл выражение
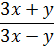
при х = 2 и y = 6?
И снова перед нами алгебраическое выражение. Ибо помимо конкретного постоянного числа (тройки), в нашем выражении тусуются ещё и буковки. Целых две — икс и игрек. Выражение более сложное. Дробь какая-то… Ну и ладно.) Чтобы справиться с заданием, достаточно самых начальных знаний алгебры. Никаких специальных правил действий с алгебраическими дробями здесь знать не нужно. Совсем.) Об этом в других, более серьёзных уроках, будет.)
Итак, мы в курсе, что под буквами икс и игрек тоже скрываются какие-то числа. Различные числа. Поэтому и буквы в задании — разные.)
В качестве конкретных значений этих различных чисел нам предложены двойка (х) и шестёрка (у).
Вот и подставляем двойку и шестёрку вместо икс и игрек в нашу дробь и смотрим, что получится-то…
Чтобы не наляпать ошибок (оно нам надо?), можно по отдельности сосчитать числитель и знаменатель. Вот и действуем.
Считаем числитель:
3х+у = 3·2+6 = 12
Ну ладно. Двенадцать так двенадцать. Так уж получилось…
Хорошо, считаем знаменатель:
3х-у = 3·2-6 = 0
Ух ты, какая забавная штука-то… А знаменатель-то нулю оказался равен! На который делить нельзя, да… Надеюсь, вы помните из арифметики, что дробь — это деление? Числителя на знаменатель?)
Вот вам и ответ: нет. Выражение не имеет смысла.
Прошу заметить одну важную вещь: наше выражение не имеет смысла не вообще само по себе, а только при предложенных значениях переменных (x=2 и y=6). При каких-нибудь других значениях букв (скажем, при x=1 и у=2) у нашего выражения смысл появляется:
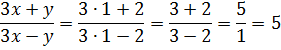
Почувствуйте разницу, как говорится!
И тут я слышу неосторожный вопрос:
А зачем нужна алгебра? Какие задачи она изучает и решает?
И правда, зачем нам вообще городить весь этот огород с числами и буквами, что-то там подставлять, да ещё и периодически посматривать, считабельно или нет?
Зачем нам вся эта символьная и буквенная схоластика… пардон… алгебра?
Вообще-то, со смысла и назначения алгебры наш урок и начинался, но, так уж и быть, отвечаю ещё раз.
Ответ:
Алгебра — мощнейший инструмент для работы с формулами! Для решения уравнений (и неравенств). И особенно — решения задач! Самых разных! Кстати, не только по математике, но и по физике, химии, экономике и другим точным наукам.)
В том числе алгебра нужна и для решения обычных житейских задач. Из реальной повседневной жизни, да.)
Например, вы решили помощь маме с папой сделать ремонт в ванной комнате.) И на складе подбираете красивую кафельную плитку, чтобы полностью облицевать пол. Скажем, площадь вашей ванной составляет 4 квадратных метра. Или 4 м2.
И вы в магазине решаете такую житейскую задачку: сколько надо заказать квадратных плиток "n" со стороной "a" см, чтобы облицевать весь пол в ванной и использовать все плитки полностью, ни одну не разрезая?
Для решения этой житейской задачки вполне достаточно обычной школьной алгебры!
Итак, нам известна площадь всей ванной комнаты. Это 4 квадратных метра. Или просто 4. Постоянное число. Также нам известна длина стороны плитки. Это "a" сантиметров. Переменная величина. Ибо длину стороны плиточки мы с вами подбираем. Не знаем мы точного значения… Поэтому вместо циферки вводим буковку, да.) И ещё есть количество этих самых плиточек "n". Тоже буковка, да. Ибо конкретного количества-то плиточек мы тоже не знаем!)
Как составить алгебраическое выражение (формулу) для решения задачи?
Подключаем житейскую логику и здравый смысл. Площадь всей ванной знаем? Знаем! Это 4 (квадратных метра). Площадь комнат в квартире она обычно в квадратных метрах измеряется, да…)
А площадь одной плиточки? Ну, раз плиточка квадратная, то по формуле площади квадрата её площадь будет a2. Но… Внимание! Квадратных сантиметров! Ибо величина стороны плитки нам дана в сантиметрах. А выразить надо — тоже в метрах!
Запоминаем раз и навсегда:
Все однотипные величины в задачах алгебры (в нашем случае это — площадь) должны быть выражены в одинаковых единицах измерения!
Иначе составленное выражение будет неверным, да…
И сколько же в одном квадратном метре квадратных сантиметров? Вопрос из начальной школы… В 1 м2 содержится 10000 см2! Прошу заметить, не 100, как многие думают, а именно 10000! Или 100 в квадрате (1002) Это значит, что 1 см2 по площади ровно в 10000 раз меньше, чем 1 м2!
Поэтому площадь одной плиточки в квадратных метрах составит вот такую величину:
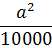
А у нас таких плиточек сколько? Конкретно — не знаем. Но в общем виде — знаем! Это n штук. Я же не зря говорил, что буквы в алгебре — это как бы числа. Только не конкретные, а подразумеваемые. Вот и умножаем эту штуковину на n! Всю целиком:
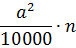
А теперь, чтобы замостить плитками пол в ванной без зазоров и разрезов, должно выполняться железное равенство:
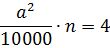
Где 4 — это наши известные четыре квадратных метра площади ванной комнаты.)
А уж выразить буковку n из полученного равенства (формулы) уже не такая большая проблема даже для нашего начального уровня. Хотя бы по правилам работы с дробями и пропорциями:
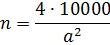
Вот мы и составили алгебраическое выражение (или более научно — формулу) для подсчёта заказываемых плиточек.
Вот оно:
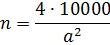
А теперь начинаем наш подбор. Подойдёт ли нам плиточка размером, скажем, a=20 см? И сколько таких плиточек понадобится заказать? Как подсчитать? Подставляем вместо буквы "a" в выражение двадцатку да и считаем:
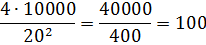
То есть n = 100. Отлично! Ровно сто плиток нам понадобится!
А если сторона плитки a=15 см? Что ж, опять подставляем и считаем:
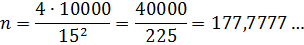
Вот-те раз! Число n получилось дробным! Житейски это значит, что покупать надо 178 плиток, но одну из них придётся резать (болгаркой, например). И не факт, что ровнёхонько получится разрезать: дробь нехорошая, периодическая… Не годится этот вариант совсем....)
А если сторона плитки 16 см?
Опять подставляем вместо буквы "а" число 16 и повторяем расчёт:
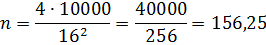
Уже получше. Понадобится 156 полных плиток и ещё четвертинка! Итого 157 плиток. А одну — распиливать на 4 части и брать один кусочек.
Улавливаете идею? Конечно же, самый лучший вариант — когда всё выражение делится нацело! В нашем случае это будет 100 плиток со стороной 20 см.
Видите, какая интересная математическая дуэль у нас с вами разразилась!
Вообще-то, то чем мы с вами только что занимались, называется составлением математической модели задачи. Или математическим моделированием. А алгебра и её методы — верный и надёжный спутник и помощник для математического моделирования и решения такого рода задачек! Намёк понятен? :) Но задачи и их математические модели — это большая тема отдельного урока… А здесь — лишь ознакомительная демоверсия.)
Вообще говоря, если более глубоко подумать, то задачка эта не такая уж и простая, как может показаться. Во-первых, кто сказал, что ванная комната обязательно должна быть именно прямоугольной формы? Это раз. Во-вторых, даже если пол и прямоугольный, то кто сказал, что его размеры обязательно делятся нацело на длину стороны плитки? Это два. Так что вопрос, придётся или не придётся какие-то плитки распиливать (и сколько конкретно плиток распиливать) зависит не только от соотношения площадей, да… Но и от формы пола и его размеров.) Но для прикидочной оценки (сколько вообще плиток заказывать) даже такого грубого подсчёта вполне достаточно.
Что, сложная задачка? Ладно, ремонт в ванной не каждый день делаем, зато за продуктами ходим регулярно. Вот вам задачка попроще. Для отдыха.) Даже не задачка, считать ничего не будем, а лишь так, поразмышляем.
Сыр стоит х рублей, а батон хлеба — у рублей. Каков смысл выражений:
а) х+у
б) 2х+3у
в) х-у
г) х:у
Вот и поразмыслим… Как вы думаете, если вы захотите купить один кусок сыра и один батон хлеба, что вы будете делать, дабы узнать стоимость всей покупки? Конечно! Вы просто сложите цену сыра (х) и цену хлеба (у)! Получится х+у. А уж сколько там сыр с хлебом конкретно стоят в рублях — от конкретного магазина или продавца зависит… А перед алгеброй все магазины и все цены равны: икс плюс игрек — и всё тут.) Вот вам и весь смысл первого выражения.
Уверен теперь, что следующее выражение 2х+3у вас уже не поставит в тупик. За продуктами все ходим.) Догадались? Да! Это будет общая стоимость двух кусков сыра (2х) и трёх батонов хлеба (3у). Улавливаете?)
А х-у? Не всех осеняет сразу… Это выражение ответит нам на вопрос: "На сколько рублей кусок сыра дороже батона хлеба?"
И, наконец, последнее выражение х:у. А за ним какой вопрос скрывается? Правильно! Во сколько раз кусок сыра дороже батона хлеба? Или: "Во сколько раз батон хлеба дешевле куска сыра?" Что одно и то же, да.)
Видите? Каков вопрос задачи, такое и алгебраическое выражение составить надо. Для конкретного вопроса — своё выражение. Но — в общем виде, через буквы. Придём в магазин, посмотрим на ценники, подставим конкретные числа и подсчитаем значение нужного нам выражения. Вот и вся суть.)
А сейчас порешаем простенькие задания самостоятельно. Для привыкания.
1. Найдите значение выражения 8х-3,7 при х = -2,6.
2. Имеет ли смысл алгебраическое выражение 10a:(5a+1) при а = -0,2?
3. Время движения лодки по течению реки задаётся формулой t = S:(х+y), где S — расстояние в километрах, х — собственная скорость лодки в км/ч и у — скорость течения реки в км/ч. Пользуясь этой формулой, ответьте на вопросы:
а) Сколько минут плыла лодка 11 км по реке с течением 0,5 км/ч и собственной скоростью 21,5 км/ч?
б) Сколько часов она будет плыть 55 км?
в) Какое расстояние в километрах она проплывёт за пять часов?
Ответы (в беспорядке через точку с запятой): 30; не имеет; -24,5; 110; 2,5.
Всё получилось? Естественно, уж проще некуда! Что-то не сошлось? Бывает… Внимательнее читаем задание! Где-то время требуется в часах, а где-то часы в минуты надо перевести, да…)
Итак, мы выяснили, что, в отличие от арифметики, в алгебре к числам примешиваются ещё и буквы. Под которыми тоже подразумеваются какие-то числа. Или даже другие выражения. А из этих чиселок и буковок уже можно конструировать самые разнообразные более сложные выражения! Алгебраические выражения.) Простейшие алгебраические выражения и базовые понятия всей алгебры — это одночлен и многочлен. Разберёмся?) В следующем уроке.
