В пробниках и методичках последних лет появилось довольно много задачек на всякие дроби, сумму или разность дробей. Обычно решаются такие задачи методом неравенств и ограничений на числа, фигурирующие в дробях. Поэтому в данном уроке мы разберём одну из таких задачек. Итак, читаем:

Перед тем, как приступать к вопросам задачи, первым делом скачаем и выпишем всю очевидную информацию из условия.
В задании сказано, что наши числа a, b, c и d — попарно различные. Что означают эти слова? Они означают всего лишь тот факт, что все наши числа — разные и ни одни из них друг другу не равны. Вот и всё.
Значит, можно записать:
a ≠ b ≠ c ≠ d.
Если продолжим читать дальше, то мы наткнёмся на слова «положительные двузначные числа». Ещё одна зацепка. Про двузначные числа мы знаем, что любое из них находится в диапазоне от 10 до 99. Так и пишем:
10 ≤ a ≤ 99
10 ≤ b ≤ 99
10 ≤ c ≤ 99
10 ≤ d ≤ 99
Ну вот. Это всё, что мы пока знаем из условия. Поехали отвечать на вопросы.
Итак, отвечаем на первый вопрос:
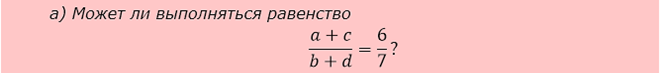
Как известно, пункт а) в таких задачах до ужаса элементарный и обычно решается простым подбором. Вот и попробуем подобрать числа a, b, c и d так, чтобы равенство выполнилось.
Здесь у многих прямо таки чешутся руки взять и подставить самые очевидные и простые числа. Что-то типа:
a = 2, b = 5, c = 4, d = 2. Тогда наша дробь как раз будет равна
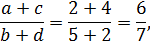
как и в задании.
Но! За такое решение вы, к великому сожалению, получите 0 баллов. Почему? Потому, что в задании сказано, что числа a, b, c и d не просто различные, но ещё и двузначные. А наши подставленные числа — однозначные. Что делать?
Что-то… Основное свойство дроби вспомнить.) Мы знаем, что числитель и знаменатель любой дроби можно умножить или разделить на одно и то же число (кроме нуля). Вопрос: на что надо умножить числитель и знаменатель нашей дроби 6/7, чтобы все четыре наших числа a, b, c, d были бы двузначными?
Давайте прикинем. В числителе у нас стоит сумма a+c. При этом, согласно требованию двузначности, как a, так и c ну никак не могут быть меньше десятки. А это значит, что их сумма никак не может быть меньше 20:
a+c ≥ 20.
На что же тогда надо домножить числитель и знаменатель дроби 6/7, чтобы в числителе получить число, большее двадцатки? Да на четыре хотя бы!
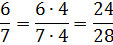
А вот теперь наши возможности выбора чисел резко расширились!
Нам нужно подобрать такие числа a, b, c и d, чтобы выполнялись равенства:
a+c = 24 (числитель),
b+d = 28 (знаменатель).
И какие же это числа? Ну, например, можно выбрать такую комбинацию:
a = 10; b = 14; c = 16; d = 12.
Тогда наша дробь будет равна:
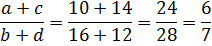
Всё точь-в-точь как и в задании. Двузначные наши числа? Да, безусловно. Различные? Конечно. То есть, условия задания полностью выполнены.
Можно было бы выбрать другую комбинацию. Например:
a = 11; b = 13; c = 10; d = 18
Какую хотите, такую и выбирайте.)
Это значит, что под пунктом а) ответ очевиден — да, может.
Ответ: Да. Например, a = 10; b = 14; c = 16; d = 12.
Как вы видите, пункт а) совсем простенький, и ответить на такой вопрос способен даже шестиклассник! Я уж молчу про старшеклассника, который в конце 11 класса сдаёт ЕГЭ.) Для положительного ответа на вопрос («Да, может») достаточно лишь предъявить подходящий набор чисел. А вот для отрицательного ответа («Нет, не может») нужно методами алгебры и арифметики убедительно объяснить, почему такого не может быть. И именно этим мы сейчас и начнём заниматься в пункте б).

Структура нашего вопроса очень простая: одно выражение в 16 раз меньше, чем другое выражение. Так и пишем:
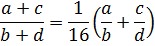
Нас спрашивают, может ли при данных условиях (числа a, b, c, d двузначны и различны) получиться вот так? Да или нет? Что ж, давайте разбираться.
Во-первых, умножим обе части равенства на 16 и приведём дроби в скобках к общему знаменателю bd. Что получим:
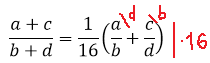
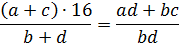
А дальше по правилу пропорции перемножаем всё крест на крест. Получаем:
16(a+c)·bd = (b+d)·(ad+bc)
Раскрываем скобки:
16abd + 16bcd = abd + b2c + ad2 + bcd
Теперь можно привести подобные и собрать всё слева:
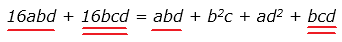
15abd + 15bcd — b2c – ad2 = 0
Что можно сделать дальше? Можно сгруппировать слагаемые. Вот так:
(15abd — ad2) + (15bcd — b2c) = 0
Дальше можно вынести в каждой скобке общий множитель. В первой скобке это ad, а во второй это bc. Выносим:
ad(15b — d) + bc(15d — b) = 0
Всё. Больше уже ничего не упростить. Что дальше? А дальше давайте рассуждать, основываясь на наших ограничениях на a, b, c и d. Очевидно, что, раз под нашими буковками скрываются положительные двузначные числа, то можно записать очевидные неравенства:
a > 0,
b > 0,
с > 0,
d > 0.
Значит, их произведения ad и bc также положительны:
ad > 0,
bc > 0.
Это понятно. А теперь попробуем оценить выражения, стоящие в скобочках. Нам, в первую очередь, надо понять, положительны они или отрицательны. Поэтому берём первое выражение 15b — d и пробуем его оценить снизу.
Мы знаем, что оба числа b и d лежат в диапазоне от 10 до 99. Рассуждаем так:
«Чтобы получить как можно меньшую разность 15b — d, нужно сделать уменьшаемое 15b как можно меньше, а вычитаемое d — как можно больше. Поэтому для оценки снизу мы должны взять нижнюю границу для b (b = 10) и верхнюю границу для d (d = 99).»
Итак, берём b = 10 и d = 99 и подставляем в нашу разность:
15b — d ≥ 15·10-99 = 150-99 = 51.
Те же самые рассуждения и выкладки проделываем и для второй скобочки:
15d — b ≥ 15·10-99 = 150-99 = 51.
О чём нам говорят эти неравенства? Мы получили, что каждая из скобочек ну никак не может быть меньше, чем 51! А это значит, что глобально каждая из наших скобочек также положительна. Раз уж она больше или равна 51.
А теперь посмотрим внимательно на наше равенство:
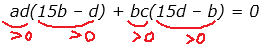
Может ли сумма положительных слагаемых оказаться равной нулю? Да ни в коем разе! Это значит, что, какими бы ни были наши чиселки a, b, c, d, такое равенство никогда не получится. Вот вам и ответ.)
Ответ: Нет.
Готово. Переходим к самому сложному пункту в).

Итак, нам дана дробь
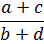
Вопрос: какое наименьшее значение может быть у этой дроби вот при таких условиях:
a>3b
c>7d?
Во-первых, мы с вами знаем, что в любом случае все наши числа лежат вот в таких диапазонах:
10 ≤ a ≤ 99
10 ≤ b ≤ 99
10 ≤ c ≤ 99
10 ≤ d ≤ 99
Такие условия (требования двузначности) у нас должны выполняться железно.
А вот теперь начнём получать ограничения на a, b, c, d уже исходя из наших дополнительных требований данного пункта. Что же у нас получится, если мы дополнительно наложим ограничения a > 3b и c > 7d? Давайте посмотрим:
Берём сначала условие a>3b. Поскольку a и b — натуральные числа, то условие a>3b можно переписать в виде нестрогого неравенства:
a ≥ 3b+1
Ну, логично. Если, например, a>30, то a≥31. Это понятно.)
Оценим теперь число a снизу. Для этого подставляем в условие
a ≥ 3b+1
самое маленькое b из возможных. Очевидно, это b = 10:
a ≥ 3·10+1
a ≥ 30+1
a ≥ 31
Число а должно быть не меньше, чем 31. Хорошо. Теперь берём второе условие c > 7d.
Это условие, в свою очередь, означает, что c ≥ 7d+1. И опять для оценки числа c снизу берём самое маленькое d. Десяточку (d = 10):
c ≥ 7·10+1
c ≥ 70+1
c ≥ 71
Вот так. Теперь мы видим, что с учётом дополнительных требований пункта в) диапазон возможных значений наших чисел a и c стал гораздо меньше:
31 ≤ a ≤ 99
71 ≤ c ≤ 99
Это была нижняя граница для чисел a и c. Хорошо. А что же с верхними границами для чисел b и d?
Опять пишем наше первое условие:
a > 3b
3b < a
Чтобы оценить букву b, берём и делим наше неравенство на три. Имеем полное право.)
b < a/3
А вот теперь вместо буквы a берём и подставляем её верхнюю границу. Это число 99:
b < 99/3
b < 33
b ≤ 32
Итак, число b при данных условиях не больше, чем 32. А изначально было не больше, чем 99.
То же самое теперь проделываем и для числа d:
c > 7d
7d < c
d < c/7
И снова вместо буквы с берём и подставляем её верхнюю границу. Это число 99:
d < 99/7
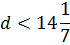
d ≤ 14 (d — натуральное!)
Готово дело. Вот наши новые диапазоны для чисел a, b, c и d с учётом всех дополнительных требований:
31 ≤ a ≤ 99
10 ≤ b ≤ 32
71 ≤ c ≤ 99
10 ≤ d ≤ 14
Как вы видите, новые ограничения на наши числа стали уже гораздо жёстче. Особенно для d — всего четыре возможных значения, что совсем немного. И вот на этом этапе многие ученики и даже учителя (конечно, из тех счастливчиков, кто до этого этапа добрался) руководствуются такими неверными рассуждениями:
«Ага, у нас есть дробь
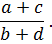
Нам теперь нужно добиться, чтобы эта дробь была как можно меньше. Для этого, очевидно, нужно, чтобы числитель дроби был как можно меньше, а знаменатель — как можно больше. Вот и возьмём для a и c их нижние границы (a = 31 и с = 71), а для знаменателя — их верхние границы (b = 10 и d = 14).
Получаем:
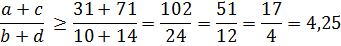
Значит, наименьшее значение нашей дроби 4,25! Ура! Задача решена!»
Вынужден разочаровать. Этот ответ 4,25 — лишь довольно грубая оценка того, что должно получиться на самом деле. В чём же дело? Дело всё в том, что, когда мы перешли к неравенству
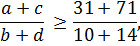
мы просто неявно подставили в нашу дробь числа:
a = 31, b = 10, c = 71, d = 14.
Но! В данной ситуации у нас нарушаются наши дополнительные условия пункта в). Вот эти:
a > 3b
c > 7d
Смотрите сами:
a > 3b
31 > 3·10 (верно)
с > 7d
71 > 7·14
71 > 98 (неверно!)
Что же делать? Чтобы данные требования у нас не нарушались, мы должны в нашу дробь вместо a и c подставить их нижние границы, выраженные через b и d. Вот эти:
a = 3b+1
c = 7d+1
Что мы тогда получим:
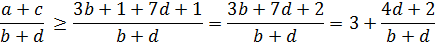
И вот теперь мы уже можем вместо d подставить её нижнюю границу d = 10 (чтобы минимизировать числитель 4d+2), а вместо b подставить верхнюю границу b = 32 (чтобы максимизировать знаменатель b+d).
Тогда получим:
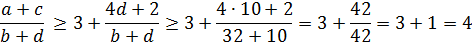
Вот так! Ровно 4, а не 4,25.
Но, прежде чем записывать окончательный ответ, нам надо показать, что это наше теоретическое наименьшее значение (четвёрка) достижимо на практике.
Для получения этого значения мы брали граничные числа:
b = 32
d = 10
Осталось найти a и с. Их мы брали в расчёте, что
a = 3b+1
b = 7d+1
Подставляем b = 32 и d = 10 и получаем:
a = 3·32+1 = 97
c = 7·10+1 = 71
Итак, именно при таком наборе чисел (a = 97, b = 32, c = 71, d = 10) у нас достигается наименьшее значение нашей дроби. Равное четырём.
Ответ: 4.
А теперь задачка для самостоятельного решения. На закрепление.)

Ответы:
а) Да (привести пример!);
б) Нет (доказать!);
в) 84/17.
