Итак, друзья, продолжаем знакомиться с задачами 19 из профильного ЕГЭ по математике! В этом небольшом уроке я расскажу о так называемой позиционной системе счисления и разберу одну интересную задачку. В чём суть.
Когда мы пишем какое-нибудь число (например, 123), мы зачастую даже не задумываемся, а как вообще они устроены! Собственно, зачем?
А на самом деле любое натуральное число (например, трёхзначное) представимо вот в таком виде:
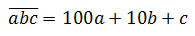
Здесь буковки a, b, c — это всего лишь цифры нашего трёхзначного числа.
При этом:
a = 1, 2, 3, …, 9
b = 0, 1, 2, …, 9
c = 0, 1, 2, …, 9
Напомню, что чёрточка сверху рисуется для отличия цифр числа от произведения abc.
Например:
123 = 100·1 + 10·2 + 3
2546 = 1000·2 + 100·5 + 10·4 + 6
И так далее. Любое натуральное число можно представить в виде такого набора переменных a, b, c и так далее. Такая традиционная запись числа называется десятичной позиционной формой записи.
В чём фишка этой формы записи числа? А фишка в том, что такая запись числа даёт нам массу возможностей. Если уметь раскладывать натуральное число в такую сумму, то можно уметь не только быстро складывать/вычитать числа, но и решать какие-то более серьёзные задачи, связанные с натуральными числами — составлять уравнения, неравенства и т.д. И успешно решать те задачи, которые, на первый взгляд, вообще не решаются!
И сейчас мы разберём одну очень красивую задачку. На настоящем ЕГЭ её не было, но она иногда попадалась в различных пробниках. И при первом взгляде на эту задачу даже у некоторых учителей глаза на лоб лезли от ужаса. Однако, на самом деле всё прекрасно решается. С помощью материала, который я вам рассказал. Итак, смотрим на саму задачу.)

Дааа, вот так задачка. Какой-то уставший (или подвыпивший) гидролог, плохая клавиатура… Сразу видно, в России работает.)
Шутки шутками, но нам задачку решать всё-таки надо, да. С чего начать? Ну, во-первых, выпишем из условия все очевидные вещи, плавающие на поверхности вместе с нашим гидрологом.
Прежде всего, измеряемая нашим гидрологом температура находится в диапазоне от 10 до 17 градусов Цельсия. В математической форме эту фразу можно записать в виде двойного неравенства. Так и пишем (можно безо всяких градусов):
10 < t < 17
Далее. Всего было сделано 32 измерения, то есть, всего таких чисел t у нас 32. Выпишем их в один ряд:
t1; t2; t3; t4; t5; …; t31; t32.
Причём (важно!) все наши температуры имеют вот такую структуру:
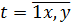
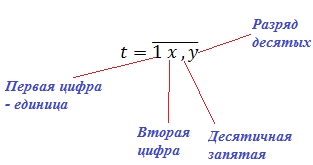
Первая цифра — всегда единица. Ну, логично, раз уж наши температуры лежат в диапазоне от 10 до 17. А вот вторая цифра и дробная часть (т.е. десятые) как-то меняются. Назовём их х и y.
И всё бы ничего, но наш гидролог из-за собственного раздолбайства допускает две ошибки.
Ошибка №1.
Один раз вместо десятичной запятой гидролог нажал клавишу «0».
Иными словами, было у нас некое число
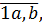
а после того, как вместо запятой гидролог поставил 0, оно стало вот таким:
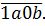
То есть, мало того, что оно у нас стало целым, так ещё аж четырёхзначным!
Ошибка №2
В другой раз гидролог вообще не нажал десятичную запятую.
На этот раз было у нас, допустим, число
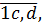
а после того, как гидролог «забил» на запятую, оно стало вот таким:
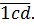
Иными словами, новое число стало трёхзначным.
Далее все наши чиселки (вместе с двумя ошибочными!) упорядочиваются в порядке возрастания. Очевидно, два тех самых ошибочных числа будут стоять в самом конце нашего ряда: на предпоследнем месте будет стоять число, где была пропущена запятая, а последним будет стоять число, где вместо запятой был поставлен нолик.
Итого имеем следующий ряд чисел:
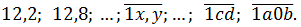
А вот теперь начинается самое весёлое, поскольку далее у нас идёт речь о средних арифметических.
Среднее арифметическое №1.
«Если из полученного ряда удалить два первых числа, среднее арифметическое оставшихся чисел будет равно 68,8,…»
Итак, берём наш ряд и удаляем два первых числа (12,2 и 12,8):
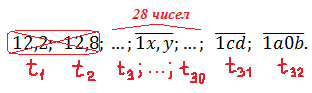
Для подсчёта среднего арифметического я обозначу сумму 28-и неизвестных нам промежуточных значений температуры t3+t4+…+t30 как S28.
Тогда наше среднее арифметическое выглядит так:
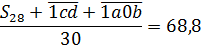
Почему мы делим не на 32, а именно на 30?
Потому, что изначально было 32 значения температуры, а два первых значения мы удалили. Осталось 30 значений температуры. Всё правильно.)
Далее самым логичным шагом было бы умножить обе части равенства на тридцатку. Вот и умножаем, т.к. лишние дроби нам ни к чему:
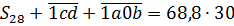
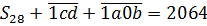
Ну вот. Первое уравнение составлено. Больше ничего здесь не упростить. Идём дальше.
Среднее арифметическое №2.
«а если удалить два последних, то среднее арифметическое оставшихся будет равно 13,7.»
Опять берём наш ряд температур, только в этот раз выкидываем два последних числа — да-да, те самые два липовых числа!
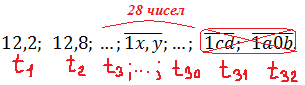
И снова считаем среднее арифметическое:
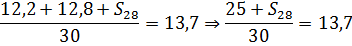
Как и в первом случае, помножив всё на 30, получим:
25 + S28 = 13,7∙30
25 + S28 = 411
Из этого простенького уравнения легко находится S28:
S28 = 411 — 25
S28 = 386
Есть! Теперь самым логичным шагом было бы подставить найденное S28 в первое уравнение. Подставляем:
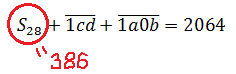
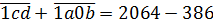
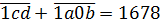
ВОТ оно, наше окончательное уравнение! А теперь призываем на помощь позиционную систему счисления. Берём наши числа и… складываем их в столбик! Да-да, вместе с буквами!
Вот так:
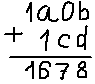
Какие ситуации при этом возможны? Ну, во-первых, очевидно, когда сумма цифр последнего разряда b и d даёт восьмёрку.
Так и пишем, в виде системы:
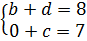
А теперь проанализируем данную ситуацию. Если b+d = 8, то в этом случае получается, что в старший разряд (разряд десятков) никакая цифра не уходит, и 0+с = 7, откуда с = 7. Но! Мы с вами знаем, что c — это цифра единиц в нашей температуре. А ограничение на нашу температуру у нас было вот такое (если кто забыл):
10 < t < 17
Из этого условия можно сделать вывод, что цифра "с" заключена вот в таких пределах:
0 ≤ с ≤ 6.
И, следовательно, должна быть строго меньше 7! А она у нас получилась в точности семёрка… Не катит! Тупик? Нет решения у задачи? Ну да, как же…
Ещё возможна другая ситуация — когда сумма последних цифр b и d даёт не восьмёрку, а восемнадцать!
Другими словами, b + d = 18.
Из этого равенства легко можно сделать вывод, что b = d = 9, поскольку ни при каких других b и d восемнадцать мы не получим: ведь b и d — это же цифры нашей температуры! Которые никак не могут быть больше, чем 9, да. А 18 можно получить лишь когда обе цифры b и d равны по девятке.
Тогда у нас получается, что b + d = 18, и единица (та самая, которая "в уме") уйдёт в разряд десятков. Тогда наша система будет такой:
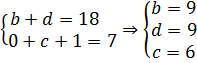
Осталось определить цифру "а". Тут уже никаких проблем:
0 + с + 1 = 7, и никакая цифра "в уме" в разряд сотен не пойдёт, поэтому можно смело записать:
а + 1 = 6, откуда a = 5.
Вот и всё! Все неизвестные циферки найдены. Осталось лишь указать нашему горе-гидрологу на его ошибки:
Первая ошибка (число, где вместо запятой был введён 0):
Вместо 15,9 введено 1509.
Вторая ошибка (число, где пропущена запятая):
Вместо 16,9 введено 169.
Ответ: вместо 15,9 введено 1509 и вместо 16,9 введено 169.
Всё, задача решена.
А теперь, в качестве разминки, вот вам задачка для самостоятельного решения. Про метеоролога.)
Метеоролог вводит в компьютер измерения температуры воздуха. Температура измеряется с точностью до одной десятой градуса, для целых значений после запятой ставится нуль. За время наблюдений температура была выше 20°С, но ниже 26°С. Всего метеоролог ввёл 22 измерения, но из-за усталости, качки судна и плохой клавиатуры один раз вместо десятичной запятой он нажал клавишу «0», а в другой раз вообще не нажал десятичную запятую. После упорядочивания данных по возрастанию получился ряд из 22 чисел, начинающийся числами 21,3; 21,7; … Если из полученного ряда удалить два первых числа, среднее арифметическое оставшихся чисел будет равно 149,53, а если удалить два последних, то среднее арифметическое оставшихся будет равно 23,28. Определите, в каких числах и какие ошибки допустил метеоролог.
