Продолжаем знакомство с аналитическими способами решения сложных задач с параметрами, предлагающихся на различных пробниках и в настоящих вариантах ЕГЭ. В сегодняшнем материале будет рассмотрена новая группа задач, связанных с поиском значений параметра(ов), при которых имеется единственное решение задачи. Слово «единственное» в данной теме является ключевым. Один из самых распространённых методов решения таких задач — так называемый метод симметричных корней или, более научно, метод инвариантностей.
Типичные формулировки таких задач следующие: «Найдите все значения параметра а, при которых система уравнений имеет единственное решение.» Или: «Найдите все значения параметра а, при которых уравнение имеет единственный корень.»
Итак, пора познакомиться с инвариантностью. Что это за понятие? В переводе на русский язык слово «инвариантность» означает «неизменяемость». Неизменяемость чего-то по отношению к чему-то.)
В математике под инвариантностью понимается неизменяемость каких-либо выражений с переменными или функций по отношению к каким-либо преобразованиям над этими самыми переменными. Это может быть замена одной переменной на другую, смена знака и т.п. На словах, быть может, звучит не совсем понятно, но на деле всё гораздо проще.
Рассмотрим простой пример. Все мы с начальной школы знаем (я верю!) переместительное свойство сложения двух чисел:
a + b = b + a.
Кто бы спорил, верно? От перестановки слагаемых сумма не меняется.) По-научному этот факт означает, что выражение a + b инвариантно относительно замены а на b и b на а. Можно сколько угодно менять буквы местами, а суть всего выражения от наших перестановок не изменится.)
Другой классический пример инвариантности – чётность. Если функция f(x) чётная, то, как мы знаем,
f(-x) = f(x),
и тогда можно сказать, что функция f(x) инвариантна относительно замены x на –x.
Посмотрим на инвариантность в жизни?
Допустим у нас есть вот такое крутое уравнение:
x + y = 10
Как нетрудно заметить, решений у него бесконечно много. Это, например, пары чисел (1;9), (5;5), (0;10), (-37;47), ну и так далее, можно писать до посинения.) Зачем, спрашивается? Пока — незачем. Бестолковое занятие, прямо скажем. Но, поскольку, как мы знаем, от перестановки слагаемых сумма не меняется, все эти решения объединяет одна важная особенность: если какая-то пара чисел (x0; y0) удовлетворяет данному уравнению, то автоматически и пара чисел (y0; x0) также обязательно ему удовлетворяет. Или в таких случаях говорят, что уравнение
x + y=10
инвариантно относительно замены x на y и y на x. Например, если пара (1;9) — решение, то автоматически и (9;1) — тоже решение. Понятно, я думаю.)
Идём дальше. Допустим, перед нами вот такая красивая система:
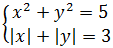
Кто умеет решать системы и в курсе, как раскрываются модули, тот без труда получит восемь её решений. Это пары:
(1; 2), (2; 1), (-1; 2), (2; -1), (1; -2), (-2; 1), (-1; -2); (-2; -1).
Чем красива эта система? А тем, что она обладает сразу тремя типами инвариантностей!
Смотрите сами.
Во-первых, суть системы не изменится от замены x на y и y на x. Это значит, что, помимо пары (x0; y0), система имеет своим решением и пару (y0; x0). Например, это пары (1; 2) и (2; 1) или (-1; -2) и (-2; -1). И так далее.
Во-вторых, квадрат и модуль — чётные функции. Это значит, что суть системы не изменится от замены, например, x на -х. Поэтому, помимо пары (x0; y0) решением системы будет являться и пара (-x0; y0). Что выражается, например, парами (1; 2) и (-1; 2). Или (2; 1) и (-2; 1).
То же самое можно сказать и про переменную игрек: суть системы не изменяется от замены y на -y, так как квадрат и модуль сжигают минус. И, помимо пары (x0; y0), решением нашей системы будет и пара (x0; -y0). Например пары (1; 2) и (1; -2).
Идея ясна?
А теперь представим, что у нас есть какая-нибудь ооочень страшная система. И мы каким-то чудом установили, что эта система инвариантна относительно, скажем, замены x на y. При этом в задаче требуется, чтобы решение было единственным. Тогда обязательно должно выполняться равенство x = y. То есть, таким единственным решением может быть только пара чисел (x0; x0) (или (y0; y0), что в данном случае одно и то же).
И теперь во всей задаче мы всюду можем смело заменить игрек на икс (или наоборот) и перейти к одной переменной, что, скорее всего, сильно упростит дальнейшие выкладки.)
Или если в какой-то задаче аргумент x всюду стоит под знаком чётной функции — квадрата, модуля, косинуса и т.п., а при этом требуется, чтобы решение задачи было единственным, то это будет возможно только в случае, когда
x = -x,
то есть,
x = 0.
Почему? Да потому, что при всех остальных x, отличных от нуля, число –x автоматически тоже будет решением, т.е. задача заведомо будет иметь более одного решения. И теперь можно подставить x = 0 в исходную задачу и существенно упростить её. Таким образом, в случае чётности имеет место так называемая симметрия относительно нуля.
Но симметрия бывает не только относительно нуля. Если, скажем, уравнение не меняется относительно замены x на 2-x и должно иметь единственный корень, то обязательно должно выполняться равенство
x = 2 — x
или
x = 1.
То есть, этим единственным корнем может быть только единица. И теперьуже можно подставить x = 1 в исходное уравнение и определить все значения параметра, при которых единица является корнем.
А бывают и менее очевидные инвариантности. Например, относительно замены x на 1/x, откуда кандидатами на единственное решение могут быть только числа ±1. И так далее. Поиск таких закономерностей — порой процесс творческий и весьма интересный, и задачи такого типа предназначены для претендентов на высокие баллы.)
Сам процесс решения таких задач состоит из четырёх ключевых шагов.
1) Осмотр задачи и выявление инвариантных конструкций. Например, выражения x и -x, y и y-1 и т.п.
2) Нахождение решений-кандидатов на единственность. Делается это путём приравнивания этих самых инвариантных конструкций друг другу и решения получившегося уравнения.
3) Подстановка решений-кандидатов в исходную задачу и поиск соответствующих этим решениям значений параметра.
4) Проверка каждого найденных значений параметра на удовлетворение условий задачи.
Четвёртый шаг очень (ОЧЕНЬ!) важен в решении таких задач! Пояснения — ниже. На примерах.
Ну ладно, длинное вступительное повествование закончено, перейдём теперь к конкретным задачам (в т.ч. и из ЕГЭ) и будем решать их по мере возрастания сложности. Начнём с малого - с уравнений. :)
Пример 1

Итак, речь идёт о единственном корне. Это явный призыв поискать в уравнении инвариантные конструкции.)
От икса зависит только левая часть. Выпишем её отдельно:
3х + 32-х.
А теперь рассуждаем примерно так:
«У нас слева стоит сумма двух показательных выражений. Основания у них одинаковые — тройка. Что очень хорошо.) А вот показатели — разные. «Икс» и «два минус икс». Но! Если в первом слагаемом показатель х заменить на 2-х, а во втором — наоборот, 2-х заменить на х, то слагаемые просто поменяются местами, а суть всего выражения при этом не изменится.»
Совершенно верно! Данное уравнение инвариантно относительно замены х на 2-х! Другими словами, если какое-то число х0 является корнем этого уравнения, то автоматически и число 2-х0 также будет его корнем. )
У нас же, по условию, корень должен быть единственным. Поэтому это возможно в том и только в том случае, когда
х0 = 2-х0
или
х0 = 1.
Здесь выявлена так называемая симметрия относительно единицы.
Это означает, что если данное уравнение имеет единственный корень, то им может быть только единица. И теперь уже можно подставить х = 1 в исходное уравнение и определить, при каких же значениях параметра а оно будет выполняться. Подставляем:
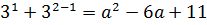
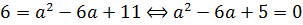
Решаем данное квадратное уравнение. Проще всего по теореме Виета:
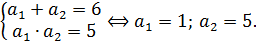
Получили два значения параметра — единицу и пятёрку. Но (внимание!) это пока что ещё не ответ, а лишь два возможных кандидата на ответ.) Теперь нам ещё предстоит сделать последний шаг — проверить каждое значение параметра а на выполнение условия единственности корня.
Специально акцентирую внимание на этом последнем шаге решения. Пропускать его ни в коем случае нельзя. Почему?
Казалось бы, всё классно: параметры найдены, и на этом решение задачи следовало бы закончить и записать ответ. Но… Вынужден открыть горькую правду. Всё дело в том, что найденные на третьем шаге значения параметра представляют собой лишь так называемое необходимое условие единственности решения. Но, к сожалению, не достаточное! Поясняю.
Найденные два числа (1 и 5) — это значения параметра, необходимые для того, чтобы единица только лишь была корнем данного уравнения. И всё! Единственный это корень будет или нет — совершенно не факт!
Поэтому последним (и обязательным!) шагом решения является проверка достаточности. Делается это так. Берётся каждое из найденных значений параметра и подставляется в исходную задачу. После чего решаем исходную задачу для каждого такого кандидата и устанавливаем, сколько решений в каждом случае получается. Тех кандидатов, при которых задача имеет более одного решения, безжалостно отсеиваем.)
Следует сказать, что последний шаг в подобных задачах зачастую наиболее трудоёмкий, потому что далеко не всегда при этом получаются уравнения и системы, решаемые стандартными алгебраическими преобразованиями — разложением на множители, приведением подобных, формулами тригонометрии, логарифмов и т.п. А требующие порой значительной изобретательности и искусства, я бы даже сказал. В чём мы лично убедимся на дальнейших примерах.)
Поэтому берём сейчас наши найденные значения параметра и подставляем в исходное уравнение.
Начнём с а = 1. Просто берём и подставляем в уравнение уже вместо «а» (а не икс!) единичку:
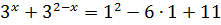
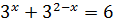
По правилам действий со степенями:
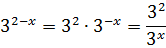
Перепишем наше уравнение с учётом данного факта:
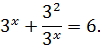
Умножим обе части на знаменатель 3х (это вполне безобидно, поскольку выражение 3х положительно при любом x и никогда не равно нулю) и перенесём всё влево:
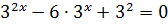
Получили квадратное уравнение относительно 3х.
Здесь даже не нужно делать замену 3х = t, а достаточно заметить, что слева стоит полный квадрат разности:
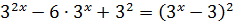
Значит,
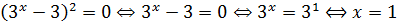 .
.
Итак, при a = 1 исходное уравнение действительно имеет своим единственным корнем единицу. Значит, a = 1 нас полностью устраивает и идёт в ответ.
Теперь разбираемся с пятёркой a = 5. Берём и подставляем в исходное уравнение пятёрку вместо a:
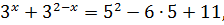
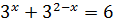
Получили уравнение, в точности эквивалентное случаю a = 1, имеющее, как уже установлено, единственный корень единицу. Значит, пятёрка нас также устраивает: a = 5.
Итак, мы полностью обосновали, что оба найденных значения параметра удовлетворяют условию достаточности, т.е. исходное уравнение действительно имеет единственный корень, и этот корень x = 1. И вот теперь можно с чистой совестью записывать окончательный ответ.)
Ответ: a=1; a=5.
Кстати, эту же задачу можно, конечно же, решить и через упомянутую выше замену переменной 3х = t, выйти на квадратное (уже относительно t) уравнение с параметром и составить условие единственности корня. Какое? Конечно же, равенство нулю дискриминанта.) Но, поскольку темой данного урока является инвариантность, то и решили мы её, используя именно инвариантность.) Всё же хорошо иметь несколько способов решения одной и той же задачи, согласитесь.)
Здесь проверка достаточности никак не сказалась на ответе. Повезло, хороший пример.) Но, ещё раз повторю, что этот шаг является обязательной частью решения таких задач. На примерах ниже мы воочию в этом убедимся.)
Пример 2
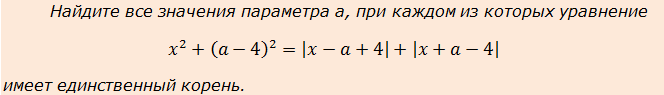
Здесь в нагрузку добавились ненавистные многими модули, но и мы тоже поднялись на следующий уровень.) Поскольку в задаче снова речь идёт о единственном корне, поищем инвариантности. Замечаем, что икс везде стоит внутри чётных функций — либо под модулем, либо в квадрате.
Напрашивается чётность. То есть, инвариантность относительно х и –х.)
Ну, с x2 всё ясно — тут чётность очевидна. А вот с суммой модулей, стоящей в правой части, всё не так очевидно. Попробуем в выражение
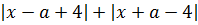
вместо «икс» подставить «минус икс» и посмотрим, что из этого выйдет:
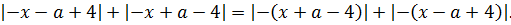
Как известно, модуль — тоже функция чётная и «сжигает» минус:
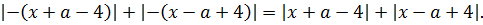
Итак, что мы видим? Мы видим, что от замены x на –x правая часть уравнения также не изменилась (просто модули поменялись местами :)). А это значит, что уравнение действительно инвариантно относительно х и –х. И, если оно имеет какой-то корень х0, то и число –х0 автоматически также будет корнем этого уравнения.
Поэтому для единственности эти два корня должны совпадать, т.е. необходимо выполнение условия
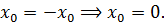
Значит, если данное уравнение имеет единственный корень, то им может быть только ноль. Подставляем число 0 в исходное уравнение вместо икса:
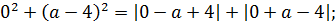
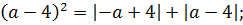
Для дальнейших упрощений воспользуемся чётностью квадрата и модуля:
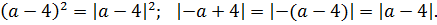
Перепишем наше уравнение с учётом этих фактов:
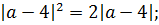
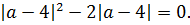
Выносим один модуль за скобку:
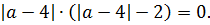
Произведение равно нулю, когда хотя бы один из множителей равен нулю:
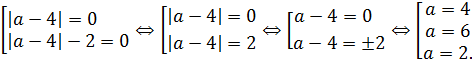
Итак, получены три кандидата на ответ. При этих значениях параметра a исходное уравнение обязательно будет иметь одним из своих корней число 0. А вот будет ли число 0 единственным корнем или нет, нам и предстоит сейчас проверить. Проверяем теперь достаточность: устраиваем нашим кандидатам конкурсный отбор. :)
Порядок здесь роли не играет. Давайте начнём с четвёрки: a = 4. Подставляем вместо а в исходное уравнение четвёрку:
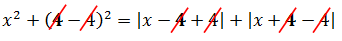
Все четвёрки благополучно посокращались и осталось лишь:
x2 = |x| + |x| или x2 — 2|x| = 0
Снова заменяем x2 на |x|2 и выносим один модуль за скобку:
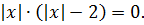
Произведение равно нулю, когда хотя бы один из множителей равен нулю:
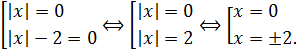
Итак, что мы видим? Мы видим, что при a = 4 наше уравнение имеет не только корень x = 0, но и ещё два корня — два и минус два! О чём это говорит? О том, что при a = 4 уравнение имеет более одного корня (а именно — целых три). Стало быть, первый кандидат a = 4 не прошёл наш кастинг, поэтому с треском вылетает из дальнейшей борьбы и в ответ не идёт. :)
Эстафета передаётся следующему претенденту a = 6. Подставляем в наше уравнение шестёрку вместо параметра a. Получаем:
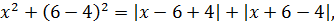
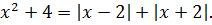
Получили типовое уравнение с модулями, решаемое путём раскрытия модулей по промежуткам. Предполагается, что народ, интересующийся нестандартными задачами с параметрами, решать такие уравнения уже умеет, поэтому здесь я опущу подробное описание решения этого уравнения (что, как, зачем и почему) и оформлю его достаточно сжато.
Как обычно, разбиваем числовую ось на промежутки, границами которых являются нули подмодульных выражений. В нашем случае это 2 и -2.
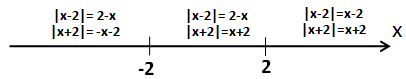
Раскроем модули на каждом промежутке и для наглядности подпишем их на рисунке.
1) x ≤ -2. Оба модуля раскрываются со знаком «минус»:
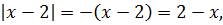
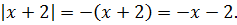
Тогда имеем следующее:
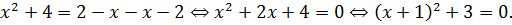
Очевидно, левая часть положительна при любых икс, а значит, данное уравнение действительных корней не имеет. Итак, на интервале (-∞; -2] корней у нашего уравнения нет.
2) -2 < x < 2. В этом случае первый модуль раскрывается по-прежнему с минусом, а вот второй - уже с плюсом:
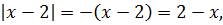
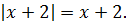
В этом случае наше уравнение станет таким:
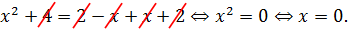
Ноль принадлежит рассматриваемому интервалу (-2; 2) и, стало быть, является первым корнем нашего уравнения.
И, наконец, на очереди третий случай.
3) x ≥ 2. В этом случае оба модуля раскрываются с плюсом:
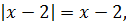
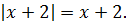
Тогда
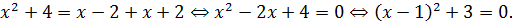
Понятно, что левая часть всегда положительна, а значит, как и в первом случае, корней при x ≥ 2 у нашего уравнения также нет.
Итак, все случаи разобраны, и единственным корнем нашего уравнения является x = 0.
А теперь вспоминаем, что это уравнение мы получили и решили для a = 6. А это значит, что при a = 6 исходное уравнение действительно имеет единственный корень x = 0, а других корней, кроме нуля, не имеет (мы только что это доказали). Всё, a = 6 нас полностью устраивает, и шестёрка пошла прямиком в ответ.)
Третий пошёл!) Подставляем теперь a = 2:
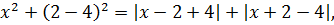
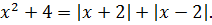
Кандидата a = 2 можно сразу принять на работу в ответ без предварительного собеседования решения полученного уравнения. Почему? А потому, что, если взглянуть на получившееся уравнение, то можно увидеть, что оно отличается от уравнения, полученного для a = 6 только порядком слагаемых в правой части. То есть, по своей сути — ничем.) И, ясное дело, оно также имеет своим единственным корнем число 0.
Итак, a = 2 тоже подходит.)
Всё, задача полностью решена! :)
Ответ: a = 2; a = 6.
Так, с уравнениями более-менее потренировались. Двигаемся на следующий уровень и переходим теперь к системам.)
Пример 3

«Так-с… Модуль, тригонометрия — всё намешано в одну кучу, что как-то не особо обнадёживает. Можно, конечно, напрямую выразить из первого уравнения игрек
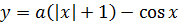
и подставить во второе, только что это даст? Всю эту белиберду ведь ещё и в квадрат возводить придётся!
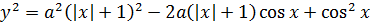
Ну, хорошо. Подставляем теперь всё это барахло во второе уравнение вместо «игрек квадрат»:
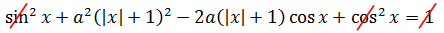
И что тут можно сделать? О-па! Да тут же основное тригонометрическое тождество sin2x + cos2x = 1, которое можно сократить с единичкой справа.)
Останется:
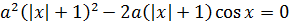
Ну, а потом что? Можно левую часть разложить на множители, отправив, к примеру, одну из скобок за скобки (да простит меня русский язык за тавтологию). Но что-то уж больно запутанно получается… Не факт, что удастся добраться до истины, совсем не факт… Стоп! Но у нас же говорится о единственном решении! А может, тут тоже есть что-то симметричное или инвариантное, что сделает решение куда проще?»
Немного присмотревшись к системе, можно снова заметить, что икс везде тусуется внутри чётных функций — модуль, косинус, квадрат синуса….
А это означает, что вместе с какой-то парой (x0; y0) данная система автоматически будет иметь своим решением и пару (-x0; y0). Что при требовании единственности решения означает, что
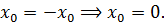
Далее по проторенной дорожке — подставляем в нашу систему х = 0 и ищем необходимые значения параметра a:
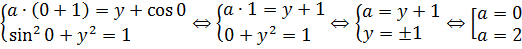
Получили два необходимых значения параметра a. Необходимых для чего? Для того, чтобы пара чисел (0; y0) была решением нашей системы. И не более того. Сколько этих решений окажется на самом деле, ещё непонятно. Что ж, снова тестируем наших кандидатов, подставляя каждого в исходную систему.)
Итак, проверяем a = 0.
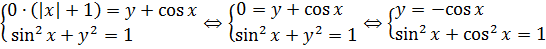
Ну,и что тут видно? Видно, что второе уравнение, после подстановки в него y = -cos x из первого уравнения, благополучно превратилось в основное тригонометрическое тождество, верное при любых значениях икса. О чём это говорит? Да! Система имеет бесконечно много решений: какой бы икс мы ни взяли, по нему всегда можно будет определить игрек из первого уравнения, а второе уравнение будет выполняться автоматически. Это значит, что при a = 0 наша система имеет бесконечно много решений. То есть, a = 0 нас заведомо не устраивает. Отметаем этого кандидата.)
Следующий клиент, a = 2.
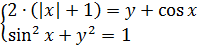
Здесь уже так просто не выкрутиться (а я предупреждал, что проверка достаточности — очень часто самая сложная часть решения задач). В таких нестандартных ситуациях, когда в уравнении слева и справа стоят какие-то разнородные (и обычно ограниченные) конструкции (в нашем случае это модуль и косинус), чаще всего применяется метод оценок или, более научно и красиво, метод мажорант. Что ж попробуем оценить каждое из уравнений.
Ну, во-первых, про модуль мы знаем, что он всегда неотрицателен:
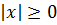 .
.
Значит, про левую часть первого уравнения можно сказать следующее:
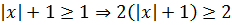 .
.
Итак, левая часть первого уравнения в любом случае не меньше двойки.
Что ещё в первом уравнении можно оценить? Ну, очевидно, косинус:
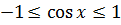 .
.
А вот всю правую часть первого уравнения мы пока оценить не можем: у нас ещё нет никакого ограничения на игрек. Ничего, сейчас получим.)
Для этого переключимся на второе уравнение:
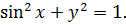
Смотрим на него и прикидываем: слева стоит сумма квадратов — двух неотрицательных слагаемых. И эта сумма квадратов даёт единицу.
А теперь подумаем: какие такие два неотрицательных числа в сумме могут давать единицу? Как нетрудно догадаться, это могут быть либо какие-то дроби от нуля до единицы (например, 0,5 или 1/3), либо же когда одно из слагаемых равно в точности нулю, а другое — в точности единице. Значит, по-любому
0 ≤ sin2x ≤ 1 и 0 ≤ y2 ≤ 1.
Раз 0 ≤ y2 ≤ 1, то тогда про сам игрек можно сказать, что -1 ≤ y ≤ 1.
Итак, мы установили ограничения на косинус и на игрек. Они таковы:
-1 ≤ cos x ≤ 1 ;
-1 ≤ y ≤ 1.
А это значит, что их сумма (т.е. вся правая часть первого уравнения) ограничена вот так:
-2 ≤ y + cos x ≤ 2.
А теперь смотрим на первое уравнение системы
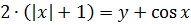
и на наши ограничения.
Для левой части: 2(|x|+1) ≥ 2, т.е. левая часть не меньше двойки.
Для правой части: -2 ≤ y + cos x ≤ 2, т.е. правая часть не больше двойки.
Как вы думаете, когда возможно равенство обеих частей уравнения? Да! Когда каждая из них одновременно в точности равна двойке!
Значит, первое уравнение системы распадается на два условия:
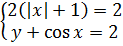
Вместе со вторым уравнением системы получим:
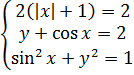
Нетрудно убедиться (а это достаточно просто), что единственным решением этой системы (а значит, и исходной) является пара чисел (0; 1). Это значит, что значение параметра a = 2 нас полностью устраивает. Всё, задача полностью решена, можно записывать окончательный ответ.
Ответ: a = 2.
Кстати, стандартный способ подстановки (размышления синим цветом в самом начале решения этого примера), который был нами прерван, здесь со скрипом, но тоже действует.) Кому интересно, попробуйте довести решение до конца, продолжив разложение на множители и приравняв каждый к нулю. :) А вот следующий пример уже куда серьёзнее будет.
Пример 4

Уже при первом взгляде на систему видно, что ничего никуда не преобразуется, переменные друг через друга «красиво» не выражаются — ни y через x, ни x через y. Значит, стандартные приёмы не катят. Но! Переменная икс у нас снова везде стоит под модулем или в квадрате, т.е. под чётными функциями! А это означает, что единственным решением данной системы может быть только пара вида (0; y0). Почему это именно так, объяснять, думаю, уже не нужно.) Если всё же непонятно, просмотрите ещё раз хотя бы предыдущий пример.
При подстановке x = 0 вся наша термоядерная система существенно упрощается:
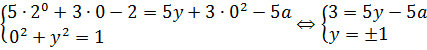
Если y = 1, то: Если y = -1, то:
3 = 5·1 — 5a 3 = 5·(-1) — 5a
5a = 2 5a = -8
a = 2/5 a = -8/5
Итак, наши кандидаты — это две пятых и минус восемь пятых. Всего два.) Это - необходимые значения параметра «a» для того, чтобы пара (0; y) была одним из решений исходной системы. Теперь, как водится, проверяем достаточность, т.е. чтобы наша пара (0; y) была не просто одним из решений системы, а единственным её решением.
Поехали, подставляем в систему a = 2/5. В этом случае вся система примет вид:
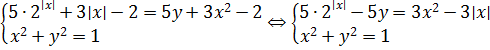
В первом уравнении я, во-первых, сократил двойки, а во-вторых, все члены с пятёркой собрал слева, а с тройкой — справа. Зачем — станет ясно ниже.)
Далее размышляем примерно так:
«Перед нами страшная система, которую как-то необходимо решить. Точнее не столько решить, сколько выяснить, сколько именно решений она имеет — единственное или нет. Или, возможно, вообще не имеет решений.) Но есть одна проблемка. Как к ней подступиться?
Если традиционно выразить y через x из второго уравнения, то будет
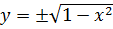
И что потом с этим плюс/минусом делать?! Непонятно…
А если выразить игрек из первого уравнения? Тогда вообще кошмар получится:
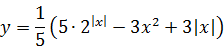
А если икс через игрек из второго? Тоже не фонтан. Значит, стандартные приёмы здесь явно не работают. Так… Но у нас в обоих уравнениях фигурируют модули и квадраты — ограниченные (снизу) конструкции. А что, если попробовать оценить левую и правую части первого (самого страшного) уравнения?»
Верные мысли! Итак, наша цель на данный момент – оценить обе части первого уравнения. Затяните потуже ремни на брюках, поскольку сейчас нам предстоит решать много неравенств. Точнее, не столько решать, сколько их выписывать, складывать, преобразовывать и т.д. Итак, перед оцениваем первое уравнение:
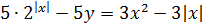 .
.
Но для начала обратим наш взор на второе уравнение:
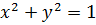
Снова, как и в примере 3, видим сумму квадратов, равную единице. О чём это говорит? О том, что каждый из этих квадратов сам по себе не превосходит 1.
То есть, 0 ≤ x2 ≤ 1 и 0 ≤ y2 ≤ 1.
То же самое можно сказать и про модули икса и игрека:
0 ≤ |x| ≤ 1 и 0 ≤ |y| ≤ 1.
Поэтому про сами x и y можно сказать, что -1 ≤ x ≤ 1 и -1 ≤ y ≤ 1.
А теперь с помощью данных неравенств оцениваем левую часть первого уравнения, равную сумме выражений 5·2|x| и -5y:
Раз 0 ≤ |x| ≤ 1, то 20 ≤ 2|x| ≤ 21 или 1 ≤ 2|x| ≤ 2.
Здесь мы воспользовались монотонным возрастанием функции f(x) = 2x.
Если теперь все три части последнего неравенства помножить на 5, то получим:
2 ≤ 5·2|x| ≤ 10
Далее, раз -1 ≤ y ≤ 1, то тогда
-1 ≤ 5y ≤ 1
и, следовательно,
-5 ≤ -5y ≤ 5.
Возможно, кому-то непонятно, как именно из неравенства -1 ≤ 5y ≤ 1 получилось неравенство -1 ≤ -5y ≤ 1. Поясняю.
-1 ≤ 5y ≤ 1 |·(-1) (умножаем обе части на -1);
1 ≥ -5y ≥ -1 (все знаки изменились на противоположные);
-5 ≤ -5y ≤ 5 (переписываем неравенство в привычной форме).
Всё!
Итак, мы установили ограничения на выражения 5·2|x| и -5y:
2 ≤ 5·2|x| ≤ 10
-5 ≤ -5y ≤ 5
Теперь, сложив почленно эти два неравенства, получим ограничение на всю левую часть целиком:
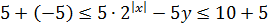
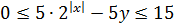
Запомним этот факт.) Обратимся теперь к правой части уравнения: 3x2 — 3|x|.
А вот её будем оценивать немного иначе.
Как нами уже установлено, 0 ≤ x2 ≤ 1.
Далее воспользуемся одним весьма нетривиальным, но очень полезным сравнением:
x2 ≤ |x| при 0 ≤ |x| ≤ 1.
Откуда я его взял? Как фокусник из рукава вытащил?)
Чтобы разобраться, почему это именно так, нарисуем графики модуля («уголок») и параболы у = x2. На отрезке [-1; 1] картинка будет вот такой:
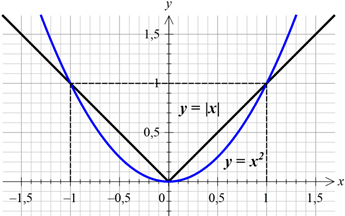
Видно, что на отрезке [-1; 1] «уголок» везде, кроме точек 0 и ±1 лежит выше параболы.
Итак, x2 ≤ |x| при 0 ≤ |x| ≤ 1.
Тогда x2 — |x| ≤ 0 (я просто перенёс модуль влево).
Значит, если это неравенство умножить на 3, то получим:
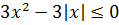
Таким образом, вся правая часть не больше нуля.
А теперь вспоминаем, что же у нас с левой частью:
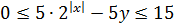
Таким образом, левая часть не меньше нуля.
Значит, равенство левой и правой частей возможно лишь в одном случае — когда каждая из них отдельно равна нулю:
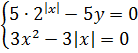
Решаем эту системку.)
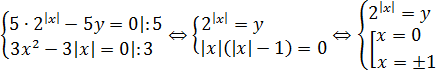
Отсюда легко получаем три пары: (0; 1), (-1; 2), (1; 2).
Однако, решения этой системы — это на самом деле лишь решения первого уравнения нашей глобальной системы.) Вспоминаем про её второе уравнение: x2 + y2 = 1.
Нетрудно убедиться, что из этих трёх пар ему удовлетворяет лишь пара (0; 1). А что это означает? В дебрях долгих выкладок и рассуждений, неволей, и про основной вопрос забываешь… ) Да! При a = 2/5 наша исходная система и вправду имеет единственное решение.
Всё, a = 2/5 обводим как часть ответа.)
А что же с a = -8/5? Делать нечего, подставляем его в нашу систему:
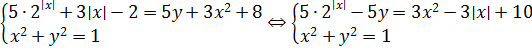
А вот здесь так красиво провести оценку уже не получится: десятка справа всё испортила.( Как быть? В таких ситуациях, как правило, приходится прибегать к самой крайней мере — попытаться тупо подбором угадать два каких-нибудь решения и таким образом доказать, что система имеет более одного решения.) Как угадывать? Ну, тут уже всё от конкретного задания зависит. И немного от интуиции и иногда от везения. В нашем случае попробуем зацепиться за второе уравнение:
x2 + y2 = 1.
Понадеемся на гуманизм составителей задания и начнём с самого простого - поищем какие-нибудь целые решения этого уравнения и подставим их в первое. Их совсем немного. Ну, например, (1; 0):
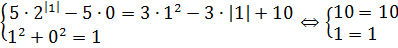
Что ещё можно проверить? Ха! У нас же симметрия по икс! Мы же как раз этот факт использовали для решения всей задачи! И думать не надо — тут же всплывает решение (-1; 0)!
Всё! Мы подобрали два различных решения системы, а это значит, что второе значение параметра a = -8/5 нас точно не устраивает. Всё, задача решена! :)
Ответ: a = 2/5.
Что ж, мы уже набрались достаточно опыта, чтобы рассмотреть какую-нибудь откровенную жесть. Берём быка за рога! :)
Пример 5
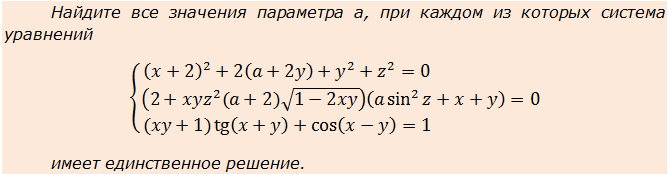
Ничего не боимся и стараемся при виде подобных монстров мыслить примерно следующим образом:
«Ух, наворотили, ужас! Корень, тангенс, синусы… Точно не решить… Так, стоп! От нас хотят найти единственное решение. Значит, скорее всего, нас просят отыскать какую-нибудь инвариантную конструкцию и с её помощью решить всю задачу.
Что тут сильнее всего бросается в глаза? Ну, во-первых, во втором и третьем уравнениях везде тусуются xy и x+y, а от перестановки множителей (слагаемых) результат не меняется. Это неспроста.) Так, ещё тут внутри косинуса затесалась разность x-y , которая от перемены икса и игрека местами сменит знак:
y-x = -(x-y).
Плохо… Так, секундочку! Но ведь косинус - чётная функция и сжигает минус! Всё отлично, под косинусом тоже ничего не поменяется!)
Но есть ещё первое уравнение. В нём пока что никакой инвариантностью относительно перестановки икса и игрека и не пахнет. А вдруг, эту инвариантность и там удастся выявить? Ну-ка, посмотрим…
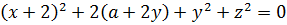
И что тут можно сделать? Можно хотя бы пораскрывать все скобки:
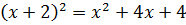
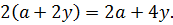
Вставляем всё в уравнение:
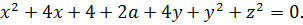
Ну, хорошо, а дальше? Сгруппируем-ка в кучку квадраты и первые степени. Хуже не будет. Будет либо хорошо, либо никак.)
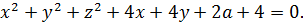
Кажется, уже что-то вырисовывается:
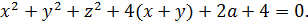
Ну, вот и выявилось то, чего мы так добивались: x2+y2 и x+y – инвариантные конструкции. Относительно замены x на y и y на x. Ура!»
Итак, вся система инвариантна относительно замены x на y (и наоборот). Это значит, что, если какая-то тройка чисел (x; y; z) является решением этой злой системы, то автоматически и тройка (y; x; z) также будет её решением! И единственность решения системы возможна только при x = y. Теперь можно во всей системе смело исключить игрек, заменив его на икс: xy превратится в x2, x+y превратится в 2x. Ну, и так далее. )
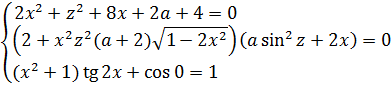
Так, система стала немного попроще, но ещё пока что довольно громоздка. Но… Переменная z везде тусуется под чётными функциями - либо в квадрате, либо внутри синуса в квадрате. А это значит, что единственность решения возможна только при z = 0. Прекрасно! Подставляем всюду ноль вместо z, и вся наша ужасная система ещё больше упростится и станет выглядеть вот так:
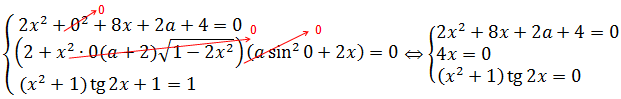
Из второго уравнения сразу ясно, что х = 0. Третье уравнение при х = 0, очевидно, выполняется. А из первого уравнения при х = 0 получим:
2a + 4 = 0, откуда a = -2.
Ух ты, как интересно! Получено одно единственное допустимое значение параметра. Минус два. Но радоваться рано, т.к. это ещё не ответ: нам же ещё достаточность надо проверить (да-да!). Деваться некуда, подставляем минус двойку в исходную систему вместо «а»:
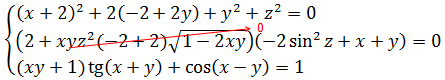
По максимуму упрощаем каждое из уравнений. В первом раскроем все скобки:
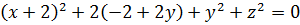
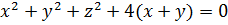
Во втором уравнении благополучно обнуляется самое ужасное слагаемое с корнем, сокращается двойка, оставшаяся от первой скобки, и остаётся лишь
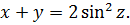
Ну, а третье уравнение так и оставим, без изменений. Итого:
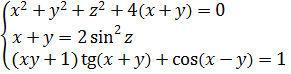
А теперь делаем такой финт ушами — подставляем в первое уравнение вместо x + y выражение 2sin2z из второго. Что получим:
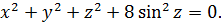
Проанализируем полученное уравнение. Чем оно примечательно? Тем, что слева стоит сумма каких-то квадратов, т.е. неотрицательных слагаемых! А когда возможно равенство нулю суммы неотрицательных слагаемых? Только в одном единственном случае — когда одновременно каждое слагаемое равно нулю! То есть:
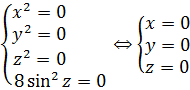
Итак, единственным решением первого уравнения является тройка чисел (0; 0; 0). Проверим эту тройку и по остальным уравнениям: вдруг, она там не пройдёт? Тогда ответом, очевидно, будет пустое множество.)
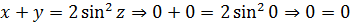
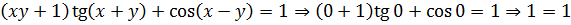
Все равенства выполнены. Итак, мы полностью обосновали, что при a = -2 наша система действительно имеет единственное решение, и это решение — «три бублика», т.е. (0; 0; 0).
Вот и всё! :)
Ответ: a = -2.
Разумеется, эти рассмотренные пять примеров далеко не исчерпывают всего многообразия параметрических задач на единственное решение и инвариантность. ) Но в них я постарался максимально подробно и доходчиво изложить, как действовать в ситуации, если, вдруг, где-то (в пробнике или в настоящем ЕГЭ) вам попалась подобная задача. Итак, подытожим тему:
1) Как только видим словосочетание «единственный корень/единственное решение» - пробуем искать инвариантные конструкции или приходить к таковым путём предварительных преобразований. Чаще всего это чётность, симметрия относительно какого-нибудь числа, либо относительно перестановок (замен) переменных или выражений.
2) Выявив тип инвариантности, составляем необходимое условие единственности решения и ищем допустимые (необходимые) значения параметра. Как правило, вся задача при этом существенно упрощается, и их поиск не составляет особого труда.
3) Проверяем найденные допустимые значения параметра на достаточность. В случае, если получаемая задача не решается стандартными методами, применяем специальные приёмы — ограниченность, монотонность и т.п. Если и они не помогают — пробуем подобрать корень или решение. Чаще всего они лежат на поверхности и, как правило, являются целыми числами.
4) Не боимся. Пробуем различные варианты.) И побольше тренируемся.) Только так можно выработать необходимый опыт в решении таких (да и вообще любых) задач с параметрами.
Всем успехов и до новых встреч!
