Для начала неплохо бы знать, что такое матрица вообще. Об этом подробно изложено в предыдущем материале.
А какие же матрицы в природе бывают? Об этом мы поговорим прямо здесь и сейчас.
Матрицы бывают разные. Чёрные, белые, красные…) Ээээ… Ну, извините, не удержался… Всякие матрицы бывают.) Принципов классификации матриц великое множество. Но основных принципов, с которыми нам предстоит работать в линейной алгебре, совсем немного. Всего два. Это классификация матриц по размерности и по условиям, налагаемым на их элементы.
Будьте готовы к тому, что в этом уроке, помимо собственно матриц, будет и немного геометрии. Самой примитивной. Для наглядности.) Итак, начнём с классификации матриц по размерности.
Классификация матриц по размерности
Например, даны вот такие четыре матрицы:
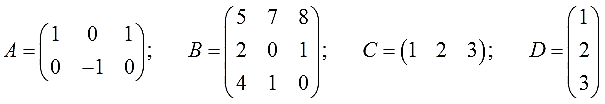
Какая размерность будет у каждой из них? Ну, с первыми двумя вопросов нет: в матрице A две строки и три столбца, а в матрице B — три строки и три столбца.
Можно записать:
A = A2x3
B = B3x3
А какая размерность будет у матрицы С? Не всех осеняет сразу…) Очень простая: одна строка и три столбца! Или 1х3. Каждый столбец матрицы С содержит всего по одному элементу. Так бывает.) С последней матрицей D всё аналогично, только наоборот — три строки и один столбец (3x1).
C = C1x3
D = D3x1
Насочинять можно ещё много чего, но общая суть классификации любых матриц по размерности очень простая. До ужаса.)
Смотрим на картинку:
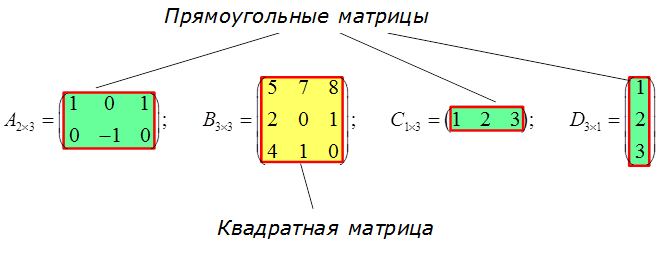
А теперь вникаем и фиксируем в памяти:
Если в матрице размерности m x n число строк НЕ равно числу столбцов (m≠n), то такая матрица называется ПРЯМОУГОЛЬНОЙ матрицей размерности m x n.
Если же количество строк и столбцов совпадает (m=n), то такую матрицу называют КВАДРАТНОЙ матрицей размерности n x n. Или, по-другому, квадратной матрицей n-го порядка.
Всё элементарно. Совпадает число строк и столбцов — матрица квадратная, не совпадает — прямоугольная.
В нашем случае матрицы A, C и D — прямоугольные, а вот B — квадратная. Размерности "три на три". Или, по-научному, квадратная матрица третьего порядка.
И все дела.)
Зачем я вообще рисую картинки, пояснения и так подробно всё расписываю? Да затем, что эти простые понятия надо усвоить железно! До автоматизма. Сами же потом спасибо скажете. На зачёте или экзамене…)
Например, квадратная матрица — важная птица в линейной алгебре! Почему? А потому, что такие важные для высшей математики операции, как, скажем, вычисление определителя и нахождение обратной матрицы возможны только для квадратных матриц! И ни для каких других. Это так, забегая вперёд.)
Отдельные названия заслужили такие прямоугольные матрицы, у которых количество строк или столбцов (или того и другого сразу) равно единичке.
Матрица, состоящая из одной строки, так и называется — матрица-строка.
Например,
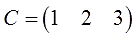
это матрица-строка размерности 1х3.
Если же матрица состоит только из одного столбца, то, вы удивитесь, она называется… как? Правильно! Матрица-столбец!)
Например,
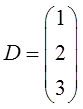
это матрица-столбец. Размерности 3х1.
По-другому матрицу-строку и матрицу-столбец называют ещё вектор-строка и вектор-столбец соответственно. А бывает и совсем коротко — просто "вектор". Именно в виде вот таких вот матриц-векторов принято записывать решения систем линейных (а иногда и дифференциальных!) уравнений. Привыкаем.)
Переходим к типам матриц по элементам.
Классификация матриц по их элементам
А вот с элементами матриц вопрос поинтереснее будет.) Ведь элементы матриц могут быть любыми действительными числами — положительными, отрицательными, целыми, дробными, иррациональными — любыми! Здесь простора для фантазии куда больше будет.
Но, так уж сложилось в процессе развития математики (и линейной алгебры — в частности), что удобнее всего людям работать с самыми простыми числами. Как можно проще! Либо с нулём, либо с единичкой. Проще чисел не найти, правда ведь? Информатика — та вообще только с нулями и единичками работает. Неспроста поди…:)
Поэтому общая идея работы с матрицами (любыми!) у нас будет такая: чем больше в матрице нулей и единичек, тем лучше! И мы в процессе изучения линейной алгебры и решения задач будем неотступно следовать этой идее настолько, насколько это возможно.)
Поэтому начнём с самых простых понятий - это нулевая матрица и единичная матрица.
Что такое нулевая матрица?
Запоминаем:
Нулевая матрица — это просто матрица, ВСЕ элементы которой равны нулю. Причём это может быть матрица любой размерности!
Всё очень просто. Нулевая матрица — это любая матрица с нулями в качестве всех своих элементов. Ни больше ни меньше. Совершенно любая. Хоть прямоугольная, хоть квадратная, хоть строка, хоть столбец - всякая.
Например:
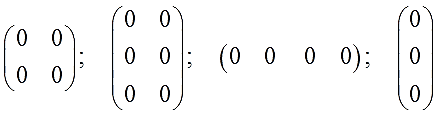
Это всё нулевые матрицы. Намёк понятен?) Любая нулевая матрица кратко обозначается буквой "О". Почти как число 0 в обычной арифметике.
Сами по себе нулевые матрицы не так интересны с практической точки зрения. Но для общей эрудиции знать не помешает. Зато следующий зверь в нашем зоопарке — единичная матрица — поинтереснее будет! К ней и переходим.)
Что такое единичная матрица?
Нет, вы не угадали.) Это вовсе не матрица, все элементы которой равны единичке. Здесь всё немножко похитрее будет.)
Хитрость номер один касается размерности единичной матрицы. Здесь всё очень жёстко. Дело в том, что любая единичная матрица, в отличие от нулевой, всегда квадратная. Скажем, два на два. Или пять на пять… И только такая! Это самое главное. Прямоугольных единичных матриц в высшей математике просто не бывает.
Хитрость номер два касается элементов единичной матрицы.
Итак, вникаем и запоминаем:
Единичная матрица — это КВАДРАТНАЯ матрица, у которой все элементы, стоящие на главной диагонали, равны единице, а все остальные элементы (вне главной диагонали) — нули.
Что такое главная диагональ? Это воображаемая линия, идущая из левого верхнего угла матрицы в правый нижний. И только так! Как при чтении книги.)
Смотрим на примере единичной матрицы "три на три":
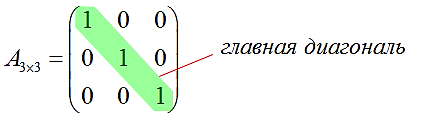
Что мы видим? Видим, что три элемента главной диагонали a11, a22 и a33 равны по единичке. А все остальные элементы, не стоящие на главной диагонали, — нули. Всё легко и просто.)
Почему, вдруг, именно эта диагональ матрицы заслужила гордое звание главной? А давайте-ка присмотримся к нумерации её элементов:
a11, a22, a33
Ну и как, просекли фишку? Да! Для всех элементов главной диагонали соответствующие номера строки и столбца совпадают! Или, что то же самое, i = j.
И так будет всегда. Для любой квадратной матрицы любого размера. В отличие от второй диагонали, для элементов которой такого удобного и красивого совпадения индексов просто-напросто не получается. Именно поэтому эта второстепенная диагональ и носит название побочной диагонали.
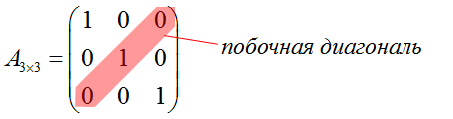
Как занумерованы элементы побочной диагонали? А вот как:
a13, a22, a31
Единичная матрица в математике обозначается заглавной буковкой "Е".
Например:
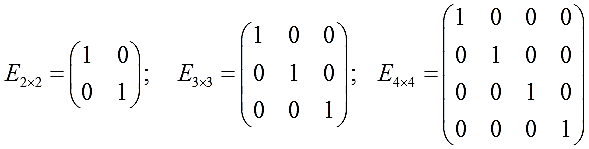
В общем, вы поняли.)
Чем же так хороша и удобна единичная матрица? Подумаешь, по главной диагонали единички проставили, а в остальных местах - нолики! Да тем же самым, чем нам удобно число 1 при работе с обычными числами! Например, от умножения числа на единичку исходное число не меняется. А от деления единички на число получаем число, обратное исходному. Удобно же, правда?)
Вот и в матрицах то же самое! Один в один. Ну… почти.) Например, от умножения матрицы А на единичную Е исходная матрица А не меняется. Об этом в теме про умножение матриц и про обратную матрицу будет.)
Ну а коли уж мы затронули такую фишку, как главную диагональ, то переходим к ещё трём типам матриц, с которыми нам предстоит встретиться на просторах линейной алгебры.
Диагональные, треугольные и трапециевидные матрицы.
Эти матрицы — важные персоны при определении таких важных вещей, как ранг матрицы и (особенно!) при решении систем линейных алгебраических уравнений. С такими матрицами в процессе этих двух увлекательных занятий мы с вами будем сталкиваться регулярно.
Знакомимся!
Что такое диагональная матрица?
Всё просто.
Диагональная матрица — это квадратная матрица, у которой все элементы вне главной диагонали — нулевые.
И всё! Есть, правда, и неквадратные матрицы, также называемые диагональными, но в 99% случаев под такой матрицей понимают всё же квадратную.
Смотрим на рисунок и всё видим:

Кстати, прошу заметить одну маленькую, но очень важную деталь. Сами диагональные элементы имеют полное право быть какими угодно — и нулевыми и ненулевыми! Например, нулевая (квадратная) и любая единичная матрица — это всё частные случаи диагональных матриц.
Чем полезна диагональная матрица? Да хотя бы тем, что такая трудоёмкая операция, как вычисление определителя, для такой матрицы осуществляется всего-навсего в одно действие! Да-да! Сами увидите.)
А определитель — очень важная штука в линейной алгебре, между прочим. Да и в аналитической геометрии, в дифференциальных уравнениях и прочих крутых разделах высшей математики тоже.)
А есть ещё такие суперкрутые штучки, как собственные векторы и собственные значения! Та ещё головная боль… Там такая матрица также будет возникать постоянно. Об этих штучках тоже в соответствующей теме подробненько будет.
Что такое треугольная матрица? Что такое трапециевидная матрица?
А такие матрицы у нас постоянно будут возникать при решении систем линейных уравнений методом Гаусса. Возможно, новичкам сейчас не очень понятно, о чём это я вообще, но если вы просто повторяете материал, то этим видам матриц здесь самое место.)
Запоминаем:
Треугольной матрицей называется любая КВАДРАТНАЯ матрица, все элементы которой над (или под) главной диагональю равны нулю.
И все дела.)
Например:
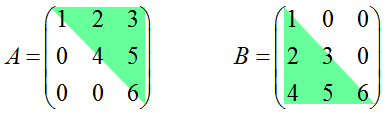
Если нулевые элементы находятся под главной диагональю, то такая матрица называется верхней треугольной матрицей. Если же нулевые элементы стоят над главной диагональю, то, соответственно, нижней треугольной.
Матрица А — верхняя треугольная. Матрица В — нижняя треугольная.
Трапециевидная матрица чуть похитрее устроена, но ненамного. Формальное математическое описание такой матрицы (через символы и индексы) в общем виде довольно занудно, а вот конкретные примеры куда нагляднее будут.
Например, такая матрица 6х6:
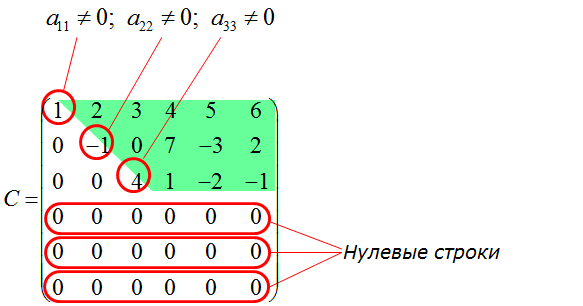
Или вот такая, 3х6:

Видно, что по размерности трапециевидная матрица может быть как квадратной, так и прямоугольной. Но все такие матрицы объединяет одна очень важная отличительная черта. Она заключается в следующем:
1. Число столбцов всегда либо БОЛЬШЕ числа строк (для прямоугольных матриц), либо РАВНО ему (для квадратных).
2. Все элементы, стоящие на главной диагонали, НЕНУЛЕВЫЕ.
3. Все элементы, стоящие НИЖЕ главной диагонали, равны нулю. При этом в матрице могут быть нулевые строки. А могут и не быть. Но, если они есть, то такие строки всегда находятся В САМОМ НИЗУ матрицы.
Зачем всё это добро нам нужно? Треугольные матрицы, трапециевидные… Ещё раз. Новичкам — пока особо незачем. Если вы только-только начинаете изучать матрицы и пока не слишком врубились — не беда. Но вот когда мы с вами дойдём до систем линейных уравнений, то с такими матрицами столкнёмся лицом к лицу. Неизбежно. И вот там я обязательно препровожу вас к изучению этого параграфа, уж будьте готовы.)
Итак, про разнообразные виды матриц поговорили. Как видим, тоже не так уж сложно. А теперь будем потихоньку учиться собственно работать с матрицами — транспонировать, складывать, перемножать, обращать и т.д. Эти темы повеселее будут.)
