Замена переменной в неопределённом интеграле, продолжение.
Снова всех приветствую, дорогие друзья! Итак, как я и обещал, продолжаем постигать, как работает процедура замены переменной в неопределённом интеграле. Вот теперь уже начинаются довольно серьёзные примеры. Тем не менее, если как следует уловить суть сегодняшнего материала, то в будущем все примеры, похожие на те, что мы здесь рассмотрим, уже не будут представлять особых проблем. Всё что будет рассматриваться в сегодняшнем материале, так или иначе, будет разложено по полочкам. Что, как, откуда и зачем. Так что устраиваемся поудобнее и вникаем.)
Вообще говоря, всевозможных замен в интегрировании существует довольно много. И, порой, весьма и весьма нетривиальных. Это и универсальная тригонометрическая подстановка, и подстановки Эйлера, Абеля, гиперболическая замена… Но пока выносить мозг раньше времени всякой экзотикой я не буду. Вот когда познакомимся с общим приёмом интегрирования рациональных дробей (и порешаем соответствующие примеры), тогда и расскажу о таких подстановках. Всему своё время. :)
Но некоторые виды замен мы вполне можем рассмотреть уже сейчас. И потренироваться на достаточно простых примерах. Нашего опыта для этого уже вполне хватает.) Так что не будем бродить вокруг да около, а лучше приступим.)
Для начала немного теории. Давайте, вкратце вспомним два предыдущих урока по замене переменной. А чуть конкретнее — как именно выглядела сама процедура в плане оформления. У нас в копилке пока что лишь два варианта. Две типовые схемы:
- подведение функции под знак дифференциала
Оформление:
1) Подынтегральное выражение f(x)dx представляется в виде произведения φ(g(x))·d(g(x)).
2) Вводится замена g(x) = t. Иначе говоря, из подынтегральной функции выделяется некая вспомогательная функция g(x) и её производная g’(x), которая затем и вносится под дифференциал, сводя исходный пример к более простому.
3) Вычисление нового интеграла, где всё выражено через новую переменную t.
4) Обратная замена и запись ответа.
- непосредственная замена переменной
Оформление:
1) Замена: "то, что не нравится" = t.
2) Дифференцирование данного равенства, установление связи между дифференциалами dx и dt.
3) Выражение всего примера через t и нахождение первообразной,
4) Обратная замена и запись ответа.
Обе эти схемы были подробно рассмотрены в двух предыдущих уроках. Кому непонятно — прогуляйтесь по ссылкам, почитайте предыдущие материалы. Там всё популярно объясняется.)
А теперь, прежде чем знакомиться с двумя интересными и красивыми заменами, рассмотрим ещё один вариант оформления. Заключается он в следующем. Вникаем.)
Пусть перед нами неопределённый интеграл
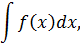
где под интегралом стоит какая-то сложная функция. Какая именно — пока неважно. Что мы делаем обычно? Либо сразу заменяем то, что нам не нравится, новой буквой, либо же вычленяем какую-то устойчивую конструкцию и подводим её под дифференциал.
А новый вариант замены здесь такой: заменяем переменную икс новой функцией φ(t). Да-да! Не просто буквой, а именно функцией! От новой переменной t.
Для полного перехода к переменной t нам, ясное дело, ещё требуется выразить через неё и наш дифференциал dx:
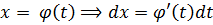
Ну вот. Подставляем теперь это всё барахло в наш интеграл и получаем новый интеграл по новой переменной t:
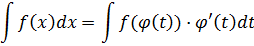
Если получившийся интеграл оказывается табличным или хотя бы проще исходного, то всё шоколадно. Мы победили!)
Как можно заметить, опять всё вертится вокруг производной сложной функции. Ничего удивительного. Вся суть замены и заключается в умении выделять сложную функцию в подынтегральном выражении, да.)
И тут я слышу закономерный вопрос: а на какую именно функцию φ(t) следует заменять икс? А вот здесь уже начинается творчество и искусство! Функцию φ(t) надо постараться подобрать таким образом, чтобы из примера исчезло всё самое нехорошее и неудобное. По максимуму. Например, если под интегралом корень, то надо добиться, чтобы корень пропал и под интегралом осталась более простая функция.
Многа букаффф, да. Ничего не поделать… Теория есть теория, да… Но запоминать наизусть всю эту абракадабру, скобочки, штрихи и не надо: на практике всё куда проще выглядит! Важно лишь понимать суть. А как именно научиться понимать суть, я сейчас и покажу. На примерах.) Итак, хватит болтовни, поехали знакомиться с нашими заменами! Первая из типовых замен, которую мы рассмотрим уже в этом уроке — это степенная замена.
Степенная замена. Интегрирование линейных иррациональностей.
Это наиболее популярная замена при интегрировании всяких нехороших функций с корнями. Суть её заключается в том, чтобы после замены из подынтегральной функции исчезли напрочь все корни. Под корнями при этом может тусоваться всё что угодно — и многочлены, и синусы, и дроби. Мы же пока рассмотрим так называемые линейные иррациональности, когда под корнем стоит линейная конструкция kx+b. Ибо такие интегралы не самые жестокие и вполне годятся для знакомства с методом. Примеров в уроке будет немного, всего три. Зато какие! Итак, решаем! :)
Пример 1
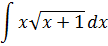
Казалось бы, простенькая функция, но… за что зацепиться? Под интегралом произведение, но интегрировать каждый множитель по отдельности — не катит. Далее. Если бы под корнем не стояло единички, то подынтегральная функция имела бы вид
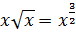
То есть, была бы обычной табличной степенной функцией с n = 3/2. А уж что надо делать со степенной функцией, мы с вами уже знаем (надеюсь). Но единичка под корнем рушит все наши мечты… Что же делать?
Надо бы как-то извернуться, чтобы и от корня избавиться, и суть примера не испортить. Всё-таки лучше, когда корня нет, правда? :) Выход только один - вводить замену. Но — какую?
Давайте соображать. Нам ведь надо избавиться от корня, верно? Вспоминаем, в результате каких действий у нас пропадает корень. Корень у нас пропадает, когда под корнем стоит точный квадрат. Надо бы наше подкоренное выражение х+1 как-то превратить в точный квадрат. Так, чтобы корень извлекался чисто! Потому что, если корень извлечётся чисто — не станет корня.)
Вот и заменим наше подкоренное выражение x+1 новой функцией t2. Тогда наш корень как раз и будет извлекаться чисто!
Итак, делаем вот такую замену: x+1 = t2.
Корень у нас квадратный, поэтому и наша новая вспомогательная функция t2 – тоже квадрат, да.)
Хорошо. Давайте теперь выражать все остальные части нашего примера через t. С использованием нашего нового равенства x+1 = t2.
Прежде всего, можно выразить сам икс: x = t2 — 1.
Вот наша вспомогательная функция φ(t) = t2 — 1, ликвидирующая так мешающий нам корень! Если бы под корнем стоял просто икс, то замена была бы такой:
х = φ(t) = t2.
А раз под корнем стоит х+1, то приходится дополнительно отнимать единичку. Всё логично.)
А теперь можно вычислить и dx:
dx = (t2)’dt = 2tdt
Так. А что же с самим корнем? А сам корень — это не что иное, как просто t! Прямо по смыслу нашей замены:
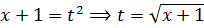
Отлично. Вставляем теперь всё в наш исходный интеграл и получаем:
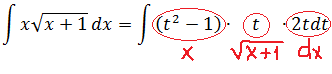
Ну, что тут можно сказать? Была под интегралом нехорошая функция с корнем, а после замены стал обычный многочлен — вполне себе благопристойная для интегрирования конструкция!) И дальнейшее интегрирование — сплошное удовольствие:
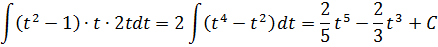
Осталось лишь вспомнить, что
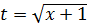
и вернуться обратно к иксу:
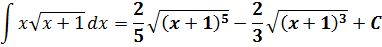
Всё. Это ответ.)
Для проверки можно продифференцировать наш результат, благо здесь это несложно:
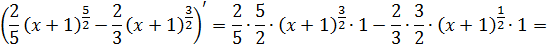
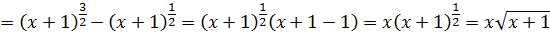
Гуд.)
Теперь рассмотрим парочку примеров с дробями.)
Пример 2
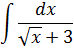
Опять анализируем нашу подынтегральную функцию. Если бы в знаменателе не было слагаемого-тройки, то наша функция была бы просто
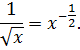
Табличная степенная функция, n = -1/2. Что делать — понятно.
Но именно наличие прибавленной тройки в знаменателе и не даёт нам возможности сразу воспользоваться таблицей. Более того, эта самая тройка вообще кардинально меняет нам весь подход к интегрированию! :) Что же делать?
Прежде всего, надо избавляться от корня. Дело уже знакомое. Заменяем подкоренное выражение (в нашем случае это х) на новую функцию t2:
x = t2
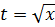
Считаем dx:
dx = (t2)’dt = 2tdt
Отлично. Теперь наш исходный интеграл по новой переменной t станет вот таким:
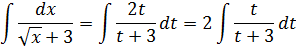
Корень снова исчез. Что и требовалось.) В прошлый раз после замены под интегралом получился многочлен, а здесь — простенькая рациональная дробь, уже безо всяких корней, что уже гораздо проще для интегрирования! Почему проще? А потому, что, забегая вперёд, скажу, что для рациональных дробей (любых!) существует свой универсальный (!) алгоритм интегрирования — метод неопределённых коэффициентов. Но… Мы его ещё не проходили, да.)
Однако, горевать не нужно, ибо в данном простеньком примере он нам совершенно не потребуется.) Как выкрутимся? Очень элегантно! Излюбленным приёмом математиков "добавить и отнять". :) Этот финт ушами мы с вами уже не раз проделывали, когда только начинали осваивать простецкое интегрирование по таблице. Вспоминайте материал предыдущих уроков!
В нашем случае, добавим и отнимем в числителе дроби тройку, выделив целую часть. Вот так:
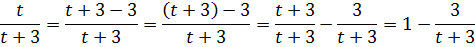
И тогда интеграл от нашей дроби распадается на разность двух совсем простеньких:
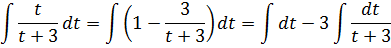
C первым интегралом от dt всё ясно, а второй интеграл в уме считается подведением знаменателя t+3 под знак дифференциала.
Вот и считаем:
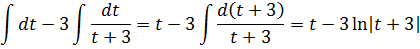
С учётом коэффициента-двойки перед интегралом:
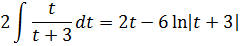
Всё! Заготовка для окончательного ответа получена. :) Осталось лишь вернуться обратно к старой переменной икс
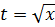
и прибавить константу С.
Получим ответ:
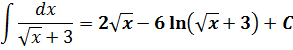
Модуль под логарифмом писать уже не нужно, ибо выражение под логарифмом положительно при любом неотрицательном икс, когда у нас определён сам корень.)
Проанализируем полученный результат. Если бы в знаменателе не стояло тройки, то наша первообразная была бы табличной и равнялась бы
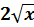
Что и выражается первым слагаемым нашего результата. Но именно наличие прибавленной тройки в знаменателе, как раз, и привело к появлению "довеска" в виде логарифма:
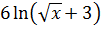
Вот так вот. :)
Не будем халтурить и продифференцируем ответ, проверим плоды наших трудов:
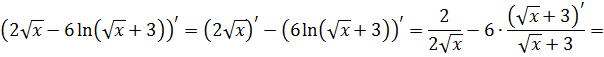
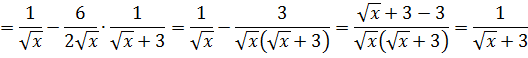
Супер!
Теперь, возможно, у некоторых читателей возник вопрос, почему я в процессе решения сразу заменяю именно само подкоренное выражение на t2, а не пишу, как обычно, по старинке:
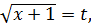
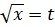
и так далее… Ведь именно корни здесь нам и не нравятся! Вот и заменили бы их сразу на t, согласно прошлому уроку, да и дело с концом…
Вопрос хороший.) Да, действительно, записи
x+1 = t2; x = t2
и
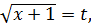
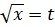
это, фактически, одно и то же. И такая традиционная запись для замены тоже имеет право на жизнь. :) Но! В подобных примерах с иррациональностями (т.е. корнями) первый вариант записи для замены (через подкоренные выражения) имеет колоссальное преимущество перед традиционным (t = "то, что не нравится"). Почему так — покажу подробно на следующем примере, который будет уже покруче. Запасайтесь попкорном. :)
Пример 3
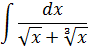
Во! В примере уже аж два корня! Причём разных - квадратный и кубический. Вопрос: что нам не нравится в примере? Квадратный корень? Согласен! Кубический? Тоже согласен! И хорошо было бы их оба как-то ликвидировать, да… Но как?
И теперь вполне естественный вопрос: что такое в примере надо заменить так, чтобы из примера пропали все корни? Вот тут некоторые могут и зависнуть.
Если, по старинке, пробовать заменять то, что не нравится, т.е. пробовать замены типа:
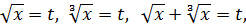
то ни в одном случае не получится полной ликвидации корней. Каждый раз будет обязательно где-то торчать либо квадратный, либо кубический корни. Попробуйте на черновике и убедитесь.)
А что, если попробовать заменить сам икс на что-то такое, чтобы все корни извлекались? Пора поразмышлять синим цветом:
«Нам надо попробовать подобрать такую замену x = φ(t), чтобы добиться полной ликвидации корней. Так как корень у нас пропадает при возведении в степень, кратную показателю корня, то наша искомая замена - некая степенная функция типа x = tn. Показатель n нам надо подобрать так, чтобы извлекались начисто как квадратный корень (2-й степени), так и кубический (3-й степени). Какое самое маленькое число делится нацело на 2 и на 3? Очевидно, 6. Стало быть, наша искомая замена:
x = t6
Вот оно чо, Михалыч! )))»
Итак, заменяем в нашем примере х на t6.
Тогда:
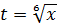
Вот так вот! Корень шестой степени! Именно такая замена уберёт нам все корни из интеграла. И попробуй, догадайся до такой замены традиционным способом! А вот способ "наоборот" x = t6 вырисовывается достаточно быстро.) Именно поэтому такое оформление замены, через икс как функцию от t, надо знать! В подобных примерах только такая замена и спасает.)
Ну вот. От корней благополучно избавились.) Теперь выражаем все остальные конструкции в примере через t:
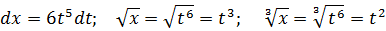
Оформляется сама замена вот так:
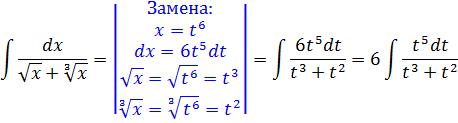
Отлично. Страшная иррациональная подынтегральная функция превратилась в рациональную дробь, с которой работать уже гораздо удобнее, чем с корнями.) Напрямую тут пока что ничего не проинтегрируешь: нужно сначала нашу дробь подготовить к интегрированию. Как? Обычными школьными преобразованиями.)
Во-первых, очевидно, можно сразу всё сократить на t2. Сокращаем:
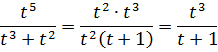
А теперь снова применяем наш излюбленный приём в дробях: добавляем и тут же вычитаем в числителе единичку и разбиваем нашу дробь на две. Формула суммы кубов нам в помощь.)
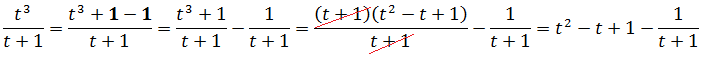
Готово дело. Теперь проинтегрировать многочлен t2-t+1 да дробь 1/(t+1) никаких проблем не составляет. Прямо в уме интегрируем:
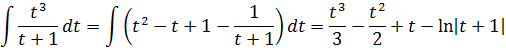
Тогда, умножая результат на 6 (шестёрка у нас вылезла в процессе замены) и прибавляя константу С, получим заготовку для нашего конечного ответа:
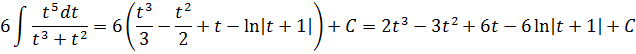
И, наконец, последний штрих — делаем обратную замену
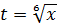
и записываем окончательный ответ:
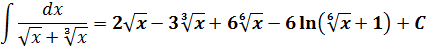
Есть.)
Желающие могут продифференцировать ответ. Проверьте! Вдруг, накосячил где-то? Тогда жду комментариев.)
Вот такие вот примеры! Всего три, но их детального разбора уже вполне достаточно, чтобы вы смогли успешно интегрировать довольно серьёзные иррациональные конструкции. Так что мы с вами уже потихонечку растём в интегрировании, накапливаем драгоценный опыт.) Подводя итог урока, дам несколько практических советов:
1) Если под интегралом стоит страшное выражение с корнем, а под корнем — линейная конструкция kx+b, то делаем замену kx+b = tn, где n — показатель корня.
2) Если под интегралом присутствуют корни разных степеней (m и n) из линейного выражения kx+b, то делаем замену kx+b = tmn, ликвидирующую все корни.
3) Если после замены под интегралом получилась рациональная дробь, в которой степень числителя больше степени знаменателя, то первым делом пробуем выделить целую часть — добавлением/вычитанием слагаемых, почленным делением и т.п. Очень часто дробь значительно упрощается и интеграл легко сводится к комбинации табличных.
А теперь — традиционная домашка. Да-да! Тренируемся и растём над собой.)
С помощью степенной замены найти неопределённые интегралы:
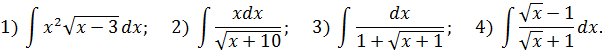
Получилось? Все примеры одной левой? Ну ладно, вот вам примеры покруче!
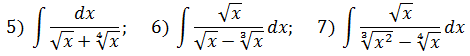
И эти на одном дыхании? Что ж, респект! Тогда ещё примерчик №8. На десерт.)
Во втором уроке по интегрированию, где мы только учились пользоваться таблицей, рассматривался пример:
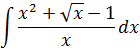
Как этот интеграл брался? Мы почленно делили на икс каждое слагаемое в числителе и интегрировали комбинацию простеньких степенных функций.
И получили вот такой результат:
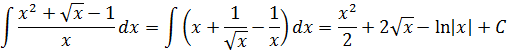
Вспомнили? Отлично!
В том примере я сделал небольшое лирическое отступление насчёт малюсенького видоизменения данной функции и к чему оно привело бы. Изменение заключалось в добавлении единички в знаменателе дроби.) То есть, наш интеграл теперь стал вот такой:
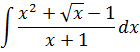
А теперь - возьмите его! Методом замены икса на t2, да.) Только так у нас есть возможность избавиться от корня.
Подскажу немного, что сначала очень полезно сделать с функцией, чтобы не надорваться и не наляпать ошибок. :)
Разложим нашу подынтегральную дробь на две и упростим:
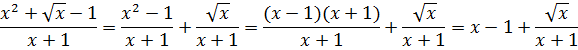
Надеюсь, что процесс интегрирования выражения x - 1 не вызовет затруднений? Ну, а оставшуюся дробь с корнем — уж будьте добры добить методом замены.)
И это получилось? Круто! Мои поздравления! :) Значит, интегрирование иррациональностей — не ваша проблема.
Не всё получилось? Ну да, в паре примеров выделять целую часть из дроби долго и нудно. Но всё решаемо. Формулы сокращённого умножения вам в помощь! И метод «добавить/вычесть». :) А если уж совсем худо — используйте деление многочленов уголком. Не помните, как делить многочлены уголком? Тяжко тогда придётся вам в интегрировании дробей… :)
Поскольку где-то результаты получаются достаточно громоздкими и проверочное дифференцирование уже достаточно трудоёмко, то, так уж и быть, в этот раз даю ответы (естественно, в беспорядке):
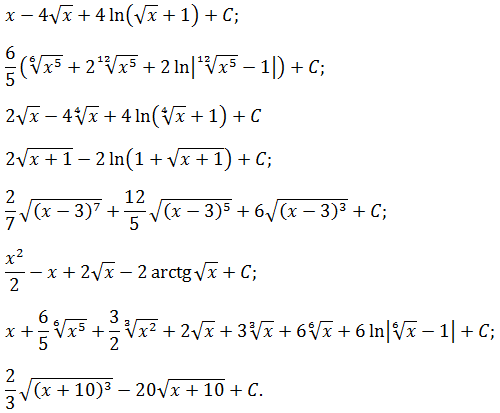
Успехов вам в интегрировании (и не только)! Продолжение следует. :)
