Операции над числовыми промежутками.
Операций над промежутками совсем немного. Всего две. Это пересечение и объединение. При решении серьёзных заданий с неравенствами эти две операции над промежутками необходимо проделывать постоянно. В самых разных сочетаниях. По своей сути это очень простые операции. Но, справедливости ради, эти самые операции являются вторым источником досадных ошибок при решении неравенств после тождественных преобразований. Разберёмся?
Пересекать и объединять числовые промежутки, проще всего при помощи числовой оси. Начнём с пересечения, оно хоть и проще в визуальном восприятии, но простора для ошибок даёт больше…
Как пересекать промежутки?
Сама по себе операция пересечения промежутков совсем простая. Тем не менее, именно пересечение промежутков — самая богатая на сюрпризы операция, которая столько людей ушибла! И очень больно ушибла. Но мы-то с вами — люди думающие и осторожные! С сюрпризами разберёмся, да и под ноги смотреть будем.) И не споткнёмся на ровном месте.
Итак, для начала запоминаем:
Пересечением двух числовых промежутков называется их общая часть.
И всё! Смутить могут только слова "общая часть". Всё просто. Общая часть — это те точки (или кусочки оси), которые одновременно входят в каждый из промежутков. Слова "общая часть" и "одновременно" здесь синонимы. Если раз и навсегда разобраться в этих нехитрых словах, то при ответе на любой вопрос о пересечении любых промежутков вы даже не заметите проблем! Намёк понятен?)
Возможно, вы до сих пор в сомнениях, но картинка с числовой осью, наш главный помощник, всё сразу же прояснит! Это только на конкретных примерах показать можно.
Начнём с совсем простенького, безо всяких подводных камней в виде выколотых точек. Допустим, нам надо пересечь два промежутка:
[-2; 6]
и
[4; +∞)
Первым делом рисуем числовую ось, отмечаем все граничные точки правильными кружочками. Они здесь — чёрные:
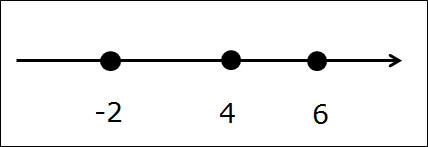
Вот так. Следующим шагом подштриховываем оба промежутка на одной оси. Чтобы не запутаться, для отличия пользуемся штриховкой с разных сторон оси в разных направлениях. Не нужно ювелирно штриховать по линеечке, мы не на черчении. Штрихуем грубо, брутально, но — разборчиво. Где-то штриховки будут встречаться одна под другой, образуя "ёлочку", но ничего не смущаемся, это — именно то, что нам и нужно! Получим такую картинку:
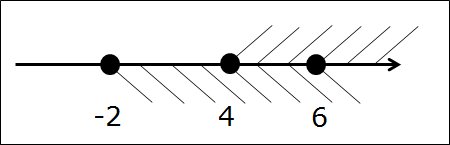
А теперь смотрим и соображаем: какой кусочек числовой оси подштрихован обоими видами штриховки одновременно? Верно! Кусочек между точками 4 и 6. Или — промежуток [4; 6]. Этот промежуток и будет пересечением промежутков [-2; 6] и [4; +∞). И все дела.)
Математически результат пересечения оформляют вот так:
[-2; 6] ⋂ [4; +∞) = [4; 6]
Значок "⋂" означает "пересечение".
Разбираем следующий пример. Пример совсем безобидный, но ступор у некоторых случается, да…)
Пересечём, например, промежутки:
[-2; +∞)
и
[4; 6]
Как видим, граничные точки (те, что будем рисовать на оси) остались прежними — это -2, 4 и 6. Кружочки также не поменялись, так и остались чёрными. Только сами промежутки — другие.
Рисуем. В этот раз я буду использовать второй способ рисования — дужки. Получим такую картинку:
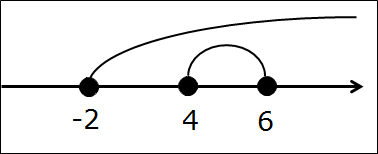
И опять соображаем: какой кусок оси содержит точки обоих промежутков одновременно?
Не догадались? Тогда снова штрихуем промежутки в разных направлениях, прямо под дужками. И смотрим, где штриховки накладываются:
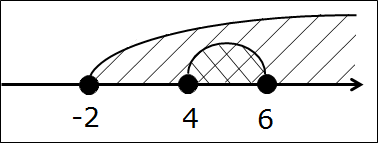
Ну и как, осенило? Да! Второй промежуток [4; 6] — и есть наше пересечение (т.е. общая часть)! Да, весь целиком. Дело всё в том, что второй промежуток, [4; 6], целиком содержится в первом [-2; +∞). Ничего страшного, так бывает.
В математической форме:
[-2; +∞) ⋂ [4; 6] = [4; 6]
Уловили идею? Ну-ка, быстренько закрепим успех!
Найдите пересечения следующих числовых промежутков:
(-∞; -3] ⋂ [-4; +∞) =
[1; 7] ⋂ [5; 10] =
[0; 8] ⋂ [1; 4] =
(-∞; 0] ⋂ [-1; 0] =
Ответы (в беспорядке):
[1; 4]
[-4; -3]
[-1; 0]
[5; 7]
Что, примитив? Ну да, проще некуда. А вот сейчас начинаются первые сюрпризы! Я же обещал…)
Сюрприз первый — пустое множество
Попробуем пересечь, скажем, такие два промежутка:
(-∞; 1] ⋂ [2; +∞)
Дело нехитрое. Рисуем ось, точки-кружочки, помечаем дужками каждый промежуток, штрихуем, всё чин-чинарём…
Получаем картинку:
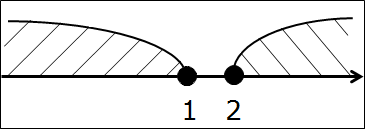
И? Где здесь общая часть? А нигде! Нету такого кусочка оси, который был бы закрашен разными штриховками одновременно. На нет и суда нет. В таких случаях говорят, что данные промежутки не пересекаются.
Математически эта фишка записывается вот как:
(-∞; 1] ⋂ [2; +∞) = Ø
Этот перечёркнутый кружочек означает "пустое множество". Множество, в котором нет ни одного элемента. Ни одного числа… Очень частое явление. Особенно — при решении систем неравенств.
Сюрприз второй — изолированная точка
Всё то же самое, что и в предыдущем примере, только двойку во втором промежутке заменю на единичку. Вот так:
(-∞; 1] ⋂ [1; +∞)
Делать нечего, опять рисуем ось. В этот раз рисуем одну единственную точку 1. Закрашенную.
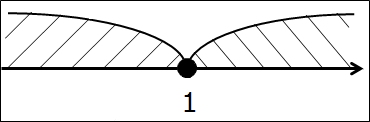
А здесь какие мысли насчёт пересечения? Да! Единственная общая часть — точка 1. Одна точка. Любая другая точка — правее ли единички, левее ли — попадает лишь в один из пересекаемых промежутков. Либо только в левый, либо только в правый. И только лишь единичка попадает в оба промежутка сразу.
В таких случаях результат пересечения (одна точка) оформляют так:
(-∞; 1] ⋂ [1; +∞) = {1}
Фигурные скобочки в такой записи означают множество. Числовое множество. Единичка внутри фигурных скобок — элемент этого множества. Один-единственный. Или — изолированная точка.
Не следует думать, что пустое множество и изолированная точка –такая уж экзотика при решении неравенств. Такие сюрпризы попадаются в системах неравенств, в методе интервалов, в нахождении области определения функции, в уравнениях/неравенствах с модулем и прочих серьёзных темах. В соответствующих уроках убедимся.)
Кто читает вдумчиво, тот заметил, что слово "множество" я употребил в этом уроке уже не один раз. И это неспроста. Дело в том, что числовые промежутки и операции над ними — это знакомство с ещё одним новым разделом математики, помимо неравенств. Раздел называется "Теория множеств" и работает именно с множествами объектов самой разной природы. Числовыми промежутками, в том числе. Но множества — отдельная большая тема. Не в этот раз…
Полдела сделано. Можно заниматься наскальной живописью. Что-то типа такого:
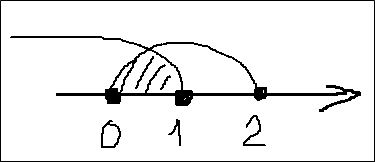
Несведущий человек отшатнётся в ужасе. А сведущий сразу твёрдой рукой напишет:
(-∞; 1] ⋂ [0; 2] = [0; 1].
Так обычно оформляют пересечение промежутков в большинстве школ. Рисуют ось, штрихуют промежутки, ищут общую часть, да и записывают ответ. Такой способ хорош только в самых простых случаях. Пока точки — чёрные.
Проблемы начинаются с появлением выколотых точек.
Как работать с выколотыми точками?
Как только в игру вступают выколотые (т.е. незакрашенные) точки, вся простота куда-то испаряется напрочь… Особенно, если одна и та же точка в разные промежутки входит по-разному. Где-то она выколота, где-то закрашена… И в каком виде рисовать её на одной оси? Закрашивать её или нет?! Вот и путается народ…
Более того, обратите внимание! Во всех примерах этого урока мы пересекаем лишь два промежутка. Для простоты и понимания сути. А в более продвинутых заданиях (системы неравенств, нахождение ОДЗ и прочие крутые штучки) приходится пересекать и три, и пять… И все с разными кружочками и скобочками… Как не запутаться?
Есть, есть один секретный способ не запутаться! Но о нём — в конце урока.
А пока фиксируем в памяти одну простую вещь:
Операция пересечения — штука жёсткая. Если точка НЕ входит хотя бы в ОДИН из пересекаемых промежутков, то она автоматически НЕ входит и в окончательный результат пересечения.
Поясняю. Если какая-то точка хотя бы в одном из промежутков является выколотой, то нас уже не волнует, что там у неё с остальными промежутками (вторым, третьим, пятым…) — входит она в них или нет: в окончательный ответ такая точка УЖЕ не войдёт. Типа, даже если вы положили в борщ картошку, морковку, свёклу, лук, но в конце посолили стиральным порошком, кушать такой борщ вы уже не будете, да…) Уловили?
Разберём ценные зелёные слова на практике. Был у нас в самом начале урока примерчик:
[-2; 6] ⋂ [4; +∞)
А теперь я немного видоизменю в нём один из промежутков. Сделаю во втором промежутке точку 4 выколотой. Т.е. скобочка перед четвёркой станет круглой. Вот такое пересечение теперь рассмотрим:
[-2; 6] ⋂ (4; +∞)
Рисуем, штрихуем, получаем картинку:
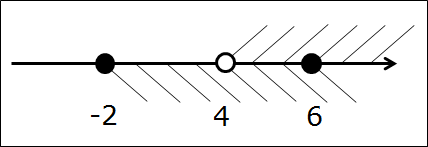
Ищем общую часть, записываем ответ:
[-2; 6] ⋂ (4; +∞) = (4; 6]
Стоп! Внимание!
Задаю вам ключевой вопрос: Почему четвёрка не вошла в окончательный ответ (4; 6], а шестёрка - вошла?
Кто в теме и врубился в слова "общая часть" и "одновременно", тот сразу всё понял. А кто не в теме, то… начинаем рассуждать. Примерно так:
"Так, берём первый промежуток (-2; 6]. Входит туда четвёрка? Разумеется! Раз уж она строго между -2 и 6. А во второй (4; +∞)? Э-э-э-э… нет! Скобочка там — круглая! Входит ли в таком случае четвёрка одновременно в оба промежутка? Нет! Во второй не вошла. Пересечение — штука жёсткая… Стало быть, и в результат пересечения четвёрка также не входит. Рисуем круглую скобочку: (4; …
А шестёрка? Тут без вопросов: в первый промежуток число 6 попадает на границу, но в закрашенном виде, а во второй (4; +∞) входит явно. Входит одновременно в оба? Да! Рисуем квадратную скобку: …6].
Итого: (4; 6]."
Вот так. Я же говорил, что ключевое слово здесь — одновременно!
Здесь-то ещё просто. А бывает куда злее! Когда неясно, как даже рисовать картинку-то… Например:
(-∞; 1) ⋂ [1; +∞)
Всё как обычно, рисуем прямую и отмечаем одну единственную граничную точку 1.
И… что-то не рисуется… В первом промежутке единичка с круглой скобкой, во втором — с квадратной. А ось — одна… Каким именно кружочком — пустым или закрашенным — рисовать единицу на оси? Непонятно…
Непонятно, если не понимать сути операции пересечения. А если понимать, то проблем — никаких. Наша граничная точка 1 в первый промежуток (-∞; 1) не входит. Выколота. Стало быть, при пересечении нам уже без разницы, закрашена ли единица во втором промежутке [1; +∞): в окончательный ответ она УЖЕ не войдёт!
Вывод: на оси точка 1 изображается выколотой. Т.е. незакрашенной.
Вот так:
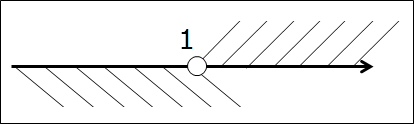
Штриховки нигде не накладываются, а единственная разделяющая точка 1 — выколота. Ответ очевиден — пустое множество:
(-∞; 1) ⋂ [1; +∞) = Ø
Обычно именно так и поступают со всеми подозрительными точками. Берут конкретную точку, поочерёдно подставляют её в каждый из промежутков, анализируют, входит/не входит, и если хоть куда-то не входит — вычёркивают отовсюду. Так рисуются все белые точки. Потом собирают все точки, которые входят одновременно во все промежутки. И рисуют чёрными… И только потом рисуют окончательную картинку… Кошмар? Согласен, кошмар. Когда ось только одна, а точек разной раскраски — много.
Поэтому сейчас мы отдохнём от писанины и тягостных раздумий. А вместо этого — порисуем. Рисовать будем много, но зато результат окупится с лихвой. А количество ошибок резко сократится.)
Обещанный секретный способ!
Пересекаем промежутки без ошибок! Метод параллельных осей.
Итак, снова пересекаем те же самые промежутки: [-2; 6] ⋂ (4; +∞).
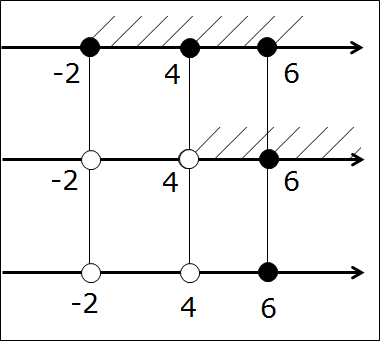
Сейчас берём в руки карандаш и рисуем… три параллельные оси! Всё правильно, именно три, я не обсчитался. На первых двух осях отдельно рисуем и штрихуем те промежутки, которые будем пересекать. Т.е. [-2; 6] и (4; +∞). На каждой из осей — свой. Соблюдаем одинаковый масштаб по всем трём осям! Это важно. Зачем нужна третья ось? Сейчас узнаем.) Получим такую картинку:
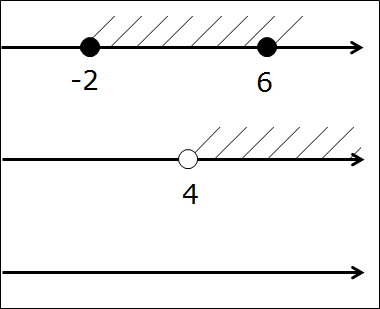
А вот теперь — самое интересное! Настал черёд третьей, пустой (пока) оси. Сейчас делаем вот что. Все граничные точки начинаем проецировать на третью ось. Как? Через все граничные точки всех промежутков проводим вертикальные прямые. Прямо насквозь. А на третьей оси — делаем засечки в виде соответствующих точек. Представьте себе, что первые две оси мы просвечиваем рентгеном, а на третьей оси у нас снимок в виде всех "засветившихся" точек.) А это -2, 4 и 6. Других точек нет.
Представили? Вот так:
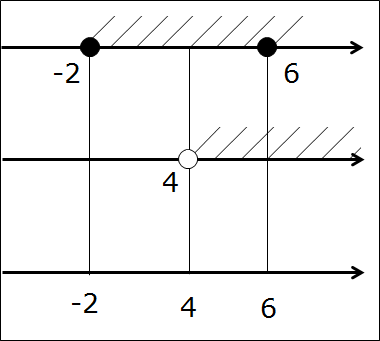
Следующим этапом фиксируем все точки соответствующими кружочками на первых двух осях. Принцип простой. Попала точка в промежуток (заштрихованную область) — значит, чёрная. Не попала — выколотая. Получаем ещё три кружочка — один белый (точка -2 на второй оси) и два чёрных (точка 4 на первой оси и точка 6 на второй). Вот так:
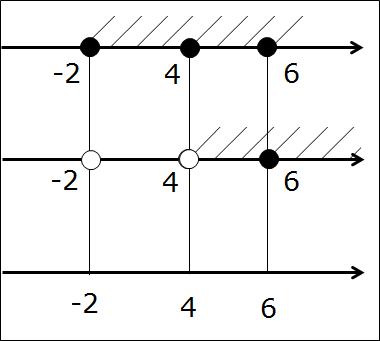
А нужны они нам — эти кружочки-то?! Ещё как! Самый ответственный, третий этап — рисуем нужные кружочки на третьей оси. Для этого рассуждаем так же, как и при прикидке в уме: если на первых двух осях обе точки чёрные, то и на третьей оси точка также чёрная. Если же хоть одна из двух точек выколота — на третьей оси точка также выколота!
Картинка станет вот такой:
Остались пустяки. Четвёртым этапом штрихуем на третьей прямой тот её кусочек, который заштрихован на первых двух прямых одновременно. Вот так:
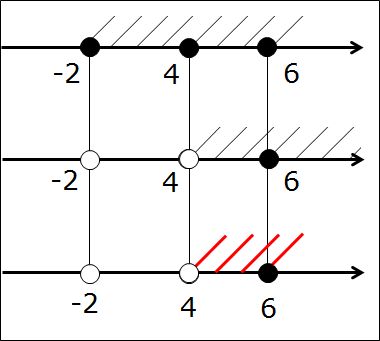
Ответ: (4; 6]
Решаем тот самый злой пример с единичкой и пустым множеством: (-∞; 1) ⋂ [1; +∞)
Рисуем картинку с тремя осями и сразу видим всю необходимую информацию:
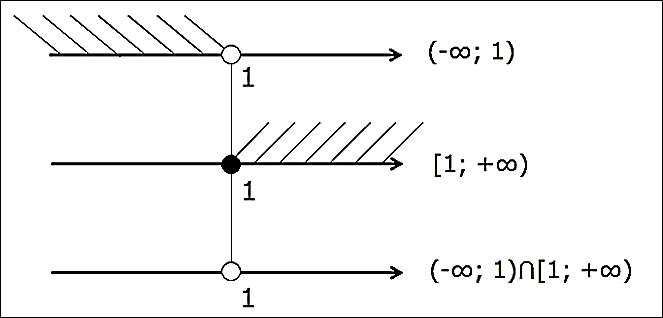
Безо всяких сомнений ясно, что единичка — выколота, а штриховать на третьей оси и вовсе нечего…
Ответ: Ø
Казалось бы, и зачем целый урок разжёвывать очевидные вещи, мог бы и в пару-тройку примеров уложиться. Но… Если бы вы знали, сколько учеников косячит при решении неравенств именно на этом этапе — какие точки включаются в ответ, а какие - нет! И не самых слабых учеников, между прочим.
Переходим к следующей важной операции — к объединению промежутков. В следующем уроке…
