Числовые и алгебраические выражения и их преобразования.
Как работать с математическими выражениями?
Допустим, перед вами пример. Хоть простой, хоть суперсложный (уравнение, неравенство, интеграл, производная и т.д….). Допустими, вы не Витя Перестукин и с математикой на "ты". Сможете, глядя на пример, сразу дать ответ?
В 99% случаев — нет. Если вы не гений математической мысли, конечно.)
Почему? А потому, что вам, так или иначе, придётся решать этот пример. Что значит "решать"? Это значит, последовательно, шаг за шагом, этот пример упрощать, добираясь до окончательного ответа. Или, по-другому, преобразовывать. Естественно, все эти фокусы (т.е. преобразования) надо проделывать по определённым правилам математики. Вот насколько успешно вы проведёте эти самые преобразования, настолько вы и сильны в математике.)
Так вот, имейте в виду: если вы не умеете делать правильные преобразования выражений, в математике вы не сможете сделать НИЧЕГО. Вообще ничего. Грустная перспектива? Вот и я так думаю.
Чтобы нас с вами не постигла столь печальная участь, имеет смысл разобраться в этой теме. Тем более тема достаточно простая. Разберёмся?:)
Что такое выражение в математике?
Выражение в математике (или — математическое выражение) — это, фактически, язык, на котором говорит вся математика. Да-да! Какую бы задачу мы с вами ни решали (хоть простую, хоть сложную), без математических выражений — никак. Любые формулы, дроби, уравнения, неравенства, синусы, логарифмы, функции, производные, интегралы и т.д. — это всё состоит из математических выражений. Намёк понятен?)
2+3 — это математическое выражение. a2 — b2 — это математическое выражение. И здоровенная дробь, и интеграл, и даже одно число или одна буковка — это всё математические выражения.
Например, уравнение:
3x+1 = 2x-5
состоит из двух математических выражений, соединённых знаком равенства "=" (равно).
Неравенство:
x2-4x+4≤0 – это тоже два математических выражения, соединённых знаком "≤" (меньше либо равно).
Короче говоря, термин "математическое выражение" применяется, чаще всего, чтобы не мычать, как корова и не кукарекать, как петух…
Спросят у вас, к примеру, что такое разность квадратов двух выражений. Первый вариант ответа: "Это ммммм… такая фиговина… Может, я лучше напишу разность? Вам какую?"
А человек в теме уверенно и с блеском в глазах ответит: "Разность квадратов двух выражений — это математическое выражение, представляющее собой произведение разности этих выражений и их суммы"!
Или: что такое квадратный корень? Квадратный корень — это математическое выражение, состоящее из подкоренного выражения и знака корня (радикала).
Согласитесь, второй вариант ответа выглядит куда более солидно и научно.)
Вот в таких вопросах фраза "математическое выражение" очень и очень удобна. Чтобы не объясняться на пальцах, как иностранные туристы в экзотической стране.
Гораздо сложнее — это конкретные математические выражения и работа с ними. Это совершенно другое дело.
Дело всё в том, что у каждого вида математических выражений имеется свой набор правил и приёмов, которому необходимо следовать при работе с ними.
У чисел — свой набор, у буквенных выражений — свой, у дробей — свой, у всяких там синусов, логарифмов, производных, интегралов — свои наборы действий. В каких-то наборах эти правила похожи или даже совпадают, а где-то — кардинально отличаются. Но пугаться этих жутких слов не надо. Эти страшные понятия мы с вами обязательно освоим в соответствующих разделах. А здесь мы с вами поработаем только с двумя видами математических выражений. А именно — с числовыми выражениями и с алгебраическими выражениями.
Что такое числовое выражение?
Что такое числовое выражение? Всё проще пареной репы.) Числовое выражение — это какое-то выражение с числами. Да-да, всего-навсего. Математическое выражение, составленное из цифр, знаков действий, скобок, знаков равенства/неравенства — это всё числовые выражения.
Например:
10-6 — числовое выражение,
(3-2,1)·0,5 — числовое выражение.
Или даже вот эти монстры:
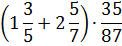
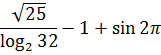
это всё числовые выражения.
Да, в последнем примере появились специальные математические символы — радикал, значок логарифма и значок синуса. Но в этом выражении тоже нет букв. Только числа! Это самое главное.
Короче говоря, любые числа, дроби, примеры на вычисление без иксов, игреков и прочих буковок — это всё числовые выражения. Намёк понятен?)
В чём главный признак числового выражения? В том, что в нём нет букв. Вообще никаких. Математические значки (если надо) — пожалуйста. А вот букв — нету. Это ключевой признак.)
Что же можно делать с числовыми выражениями? Числовые выражения, как правило, можно (и нужно) считать. Для этого, бывает, приходится менять знаки, раскрывать скобки (или наоборот, заключать в скобки), сокращать, выносить общий множитель, раскладывать на множители т.д. То есть, делать преобразования числовых выражений. Но о преобразованиях выражений — чуть позже. Терпение, друзья.)
А здесь мы с вами разберёмся с одним забавным случаем, когда с числовым выражением делать ничего не надо. Совсем! Эта приятная операция (ничего не делать)) производится, когда числовое выражение не имеет смысла.
Понятное дело, что если мы с вами напишем какую-то белиберду типа 4+)-(=), то делать ничего и не будем. Ибо непонятно, что с этим делать. Ну, разве посчитать количество скобочек.)
Однако, попадаются в математике и внешне вполне себе благопристойные выражения.
Например, такое:
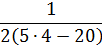
Однако это числовое выражение тоже не имеет смысла. Почему? А потому, что если выписать отдельно знаменатель дроби да посчитать, получается ноль. На который делить нельзя. Нет такой операции в математике!
Или вот такое:
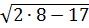
И это выражение тоже не имеет смысла! Догадались? А вы посчитайте, что под корнем получится.) Минус единичка там получится. А извлекать квадратный корень из отрицательных чисел в средней школе не учат (а вот в ВУЗе — пожалуйста). Это тоже запретное действие в (школьной) математике.
Конечно, чтобы сделать такое умозаключение, пришлось потрудиться и посчитать, что в знаменателе да под корнем получится. А в примерах может быть такого понаворочено, что… Тут уж ничего не поделаешь.)
Короче говоря, числовое выражение не имеет смысла тогда, когда в результате преобразований этого самого выражение получается запретное действие. Запретных действий в математике не так уж много: это деление на ноль, извлечение корня чётной степени из отрицательного числа, ограничения в логарифмах, в тригонометрии и в арках. Это обсуждается в соответствующих темах.
Итак, что такое числовое выражение — вникли (надеюсь).
Когда числовое выражение не имеет смысла — осознали.
Пора двигаться на следующий уровень.)
Что такое алгебраическое выражение?
Если в игру дополнительно вступают буквы, то выражение становится… Да! Оно становится алгебраическим выражением!
Например:
a+6, x+y, 2a/b, c2 + 9, x2+2x+1
В общем, вы поняли…
Понятие алгебраическое выражение — более широкое, чем числовое. Почему? Потому, что в понятие алгебраические выражения входят и все числовые тоже. То есть, любое числовое выражение — это и алгебраическое выражение. Только без букв. Типа всякий русский — россиянин, но не всякий россиянин — русский.)
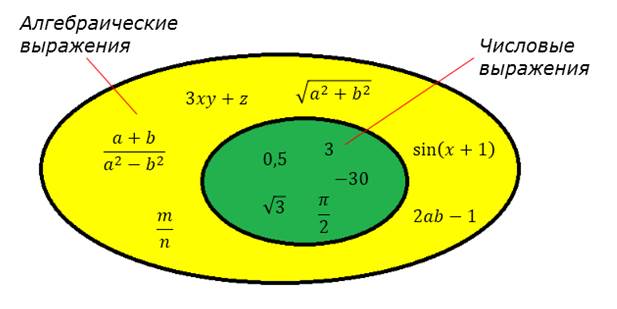
Такие выражения ещё называют выражениями с переменными. Или просто буквенными выражениями. Почему буквенное — ясно, надеюсь. Ну, раз буквы есть.) Фраза "выражение с переменными" тоже не требует особого умственного напряжения. Если, конечно, понимать, что под буквами могут скрываться различные числа. Всякие могут скрываться: и 5, и -30 — всё что угодно. То есть, букву в алгебраическом выражении можно заменять на разные числа. Какие хотим.
В выражении х+6, например, буква икс — переменная величина. Или коротко — переменная. В отличие от шестёрки, которая — величина постоянная. Или коротко — постоянная.
Что означает термин "алгебраическое выражение"? Он означает, что, в отличие от арифметики, (которая, как известно, работает только с числами), мы должны использовать законы и правила алгебры. Непонятно? Поясняю на несложном примере:
2·3 = 3·2
Что можно сделать? Посчитать и всего делов-то.) Слева шестёрка и справа тоже. А для каких-нибудь других чисел такое выполняется? Тоже можно посчитать и сравнить. Но чисел в математике — бесконечное количество. И что же? Каждый раз считать и сравнивать?!
А вот если мы шагнём из арифметики в алгебру и распишем данное равенство через алгебраические выражения:
ab = ba,
то мы сразу решим все вопросы! Для всех чисел махом! Мощная штука — алгебра.)
А когда алгебраическое выражение не имеет смысла? Что такое ОДЗ?
С числовыми выражениями всё ясно. Там на ноль делить нельзя да корни извлекать из отрицательных чисел, ну и некоторые другие логарифмические/тригонометрические фишки. А тут как узнаешь, на что делим или из чего извлекаем…
Очень просто! Точно так же!
Возьмём, к примеру, алгебраическое выражение:
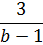
Имеет ли оно смысл? Бэ-то любое число… Любое-то любое… Но есть среди этого бесконечного набора чисел такое значение b, при котором это выражение точно не имеет смысла. Догадались? Да! Это единичка (b=1). Если в знаменателе дроби заменить переменную b (как по-школьному говорят "подставить") на единичку, то в знаменателе нолик получится. На который делить нельзя. Вот и получается, что наше выражение имеет смысл при любом b, кроме единички.
А остальные b подставлять можно? Конечно! Хоть 5 возьмите, хоть -100 — наше выражение иметь смысл будет. В таких случаях говорят, что выражение имеет смысл при любом b , кроме 1.
И вот этот самый весь остальной набор чисел, которые можно подставлять в данное выражение, и который не приводит к запретному действию, в математике называется областью допустимых значений (ОДЗ) выражения. В нашем примере областью допустимых значений (ОДЗ) служат все числа, кроме единички.
Другой пример:
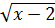
Видим квадратный корень. Сразу соображаем (из теории, т.е. основ), что корень квадратный извлекается только из положительных чисел и нуля. А вот из отрицательных — ни в какую!
Вот и обезопасим себя вот такой записью:
x-2≥0
x≥2
Таким образом, данный хитрое выражение имеет смысл лишь при иксах, больших (или равных) двойке. Число, скажем, 3, вполне себе прокатит, а вот ноль — никак нет: он меньше двойки. ОДЗ — штука жёсткая!
Уловили принцип? Внимательно смотрим на выражение с переменными, ищем опасные места и смотрим, при каких переменных получается запретная операция. И исключаем эти значения из ОДЗ.
А потом внимательно читаем задание. Чего хотят-то? Внимательное чтение никто не отменял, да… Если в задании спрашивают, при каких значениях переменной выражение имеет смысл, то ответом будут служить все значения, кроме запретных.
Или наоборот: при каких значениях переменных выражение не имеет смысла? Тогда найденные запретные значения и будут служить ответом к заданию. Почувствуйте разницу, что называется.)
А теперь вопрос к размышлению. А зачем нам смысл выражения? Есть он, нет его… Какая разница? Дело всё в том, что это понятие становится крайне важным в старших классах! Да и в ВУЗе тоже. Без этого важного понятия вы не сможете проделывать такие простые операции, как нахождение области определения функции, ОДЗ уравнений, неравенств. Что неизбежно будет приводить к полному провалу и непониманию всех этих серьёзных тем. Увы.)
Итак, самое главное из сегодняшнего урока:
1. Числовое выражение — это выражение с числами (т.е. без букв).
2. Если, помимо чисел, в выражении есть буквы, то оно называется алгебраическим выражением.
3. Как числовое, так и алгебраическое выражение, может иметь смысл, а может и не иметь. При встрече с алгебраическим выражением первым делом ищем его ОДЗ.
4. Все допустимые значения переменной (переменных), не приводящих к запретному действию, составляют Область Допустимых Значений (ОДЗ) алгебраического выражения. При необходимости ищем её!
Ну а в различных видах преобразований выражений мы с вами подробненько разберёмся и плотно поработаем в следующих уроках этого раздела.)
