Формулы сокращённого умножения необходимы во всех разделах математики. От элементарной до высшей. Они применяются практически везде — в упрощении выражений, решении уравнений и неравенств, сокращении дробей, вычислении пределов, решении интегралов — список можно продолжать ещё долго…
Следовательно, нужно основательно разобраться с этими формулами. Понять, откуда они берутся, зачем они нужны, как их применять на практике и, самое главное, как их запомнить. А запомнить всё-таки придётся, да…
Поехали?
Квадрат суммы, квадрат разности, разность квадратов, куб суммы, куб разности, сумма кубов, разность кубов — что за звери?
Итак, вот они, формулы сокращённого умножения:

Эти семь формул — полный джентльменский набор. Последние две формулы (сумма и разность кубов) записаны не так как в большинстве учебников, а наоборот — справа налево. Это не просто так.) Любая формула в математике работает в обоих направлениях — как туда, так и обратно. Именно такая запись наиболее наглядно показывает, откуда берутся формулы сокращённого умножения.
Они берутся из… умножения. Вот ведь удивил, да?) Что ж, смотрите сами. Берём, например, самую первую формулу по списку:
(a+b)2 = (a+b)(a+b) = a2+ab+ba+b2 = a2+2ab+b2
Вот и все дела. Самое обычное перемножение скобок и приведение подобных. Именно так и получаются все формулы сокращённого умножения. Сокращённое умножение — потому, что в самих формулах нет раскрытия скобок и приведения подобных. Эти промежуточные действия сокращены. Сразу дан готовый результат. Пользуйтесь на здоровье!
Эти формулы надо знать наизусть. Без знания первых трёх формул, с квадратами, даже не мечтайте о тройке! Без всех остальных (с кубами) — о четвёрке и выше. Нет-нет, бросаться зубрить весь этот список прямо сейчас мы не будем.) Об этом позже. Пока просто знакомимся.)
Зачем нужны формулы сокращённого умножения?
Полезная вещь первая — самая очевидная. Это быстрое (т.е. сокращённое) умножение многих алгебраических выражений без промежуточных выкладок. Меньше выкладок — меньше и ошибок. Но это не самая главная полезная вещь! А вот вторая.
Дело в том, что вся математика строится на преобразованиях выражений. Вся! От школьной до высшей. Сообразил, что, где и как преобразовать и упростить — решил пример. Не сообразил — увы, не решил. Есть, допустим, выражение (a-b)(a+b). Как его можно преобразовать? Да просто тупо перемножить скобки и привести подобные. Не вопрос.) А вот что делать с a2–b2? Чему это равняется? Попробуй, догадайся! Только знания и спасают, да…
Сравним два равенства:
(a-b)(a+b) = a2–b2
и
a2–b2 = (a-b)(a+b)
Для математики эти два равенства абсолютно одинаковы. А вот для нас с вами — не совсем. Возьмём первую запись, слева направо:
(a-b)(a+b) = a2–b2
Это самое обычное умножение скобок, не более того. Никаких принципиально новых возможностей. А теперь возьмём второй вариант того же равенства, справа налево:
a2–b2 = (a-b)(a+b)
А вот такая запись резко повышает уровень вашей математической культуры! Почему? Потому, что такая запись формулы, справа налево, — это разложение на множители! А разложение на множители — процедура поважнее простого умножения, да…) Сомневаетесь? Не надо. В соответствующей теме подробно расскажу.)
И такое разложение на множители имеет место быть во всех формулах сокращённого умножения! Почему? Давайте внимательно посмотрим на наш список. В левой части каждой формулы мы увидим перемножение скобок:
(a+b)2 = (a+b)(a+b) =…
(a-b)2 = (a-b)(a-b) = …
(a-b)(a+b) = …
(a+b)3 = (a+b)(a+b)(a+b) =…
и т.д.
Стало быть, левая часть каждой формулы разложена на множители, а вот правая часть — нет. Список, что приведён выше, — это, действительно, всего лишь сокращённое умножение. Но! Стоит только поменять местами левую и правую части каждой из формул, как тот же самый список становится формулами разложения на множители!
Для полного понимания перепишу этот список ещё разок, но справа налево. Вот так:

Такая обратная запись формул сокращённого умножения идеально подходит для разложения на множители многочленов, для сокращения алгебраических дробей и для решения самых разнообразных примеров. Но есть существенная проблема. Как их запомнить?
Запоминаем формулы сокращённого умножения! Секретные приёмы…
Начинаем с самого простого — запоминаем названия формул. Это совсем легко. Смотрим в таблицу и видим выражение (a+b)2. Или квадрат скобок. А в скобках что? Правильно, сумма! Стало быть, выражение (a+b)2 называется квадрат суммы. Аналогично, (a-b)2 называется квадрат разности. Элементарно, Ватсон!
С выражениями (a+b)3 и (a-b)3 всё то же самое — куб суммы и куб разности соответственно.
А как назвать a2–b2? "Одно выражение в квадрате минус другое выражение в квадрате?" Точно, но слишком уж длинно. Зато разность квадратов — и точно, и кратко!
Надеюсь, что названия сумма кубов и разность кубов у вас уже не вызовут недоумения?
А вот теперь начинается самое сложное — запоминание самих формул, со всеми этими выражениями. К сожалению, здесь тот самый случай, когда без механической памяти не обойтись. Это огорчает.
Однако здесь у нас с вами тайные знания! Эти знания помогут вам побыстрее сориентироваться во всех этих скобках, плюсах/минусах, квадратах/кубах, сведя механическую зубрёжку к минимуму. Читаем дальше и вникаем.
Итак, начинаем с квадрата суммы:

Просто медитировать, сверля формулу взглядом, будет недостаточно. Для лучшего запоминания настоятельно рекомендую выучить (да-да, именно выучить!) словесную формулировку:
Квадрат суммы двух выражений равен квадрату первого выражения ПЛЮС удвоенное произведение первого выражения на второе ПЛЮС квадрат второго выражения.
Эта мантра реально облегчает жизнь во многих разделах школьной математики! Да и в институте, при работе со всякими там пределами да интегралами, тоже. Ещё не раз вспомните эту формулировку добрым словом!)
Если вы запомнили квадрат суммы, то дальше будет проще. Можно включать логику и здравый смысл. Переходим к квадрату разности:

Сравните с квадратом суммы! Нашли отличие? Да! Перед удвоенным произведением появился минус. Ведь должен же он где-то появиться?! Перед a2 и b2 он появиться никак не может, ибо любое число в квадрате есть число положительное. Остаётся только серединка.) Для понимания рекомендую просто перемножить скобки сами на себя да привести подобные. И тогда у вас пропадут все вопросы.
В словесной расшифровке:
Квадрат разности двух выражений равен квадрату первого выражения МИНУС удвоенное произведение первого выражения на второе ПЛЮС квадрат второго выражения.
Разность квадратов:

Эта формула обычно и так легко запоминается. Единственное, можно случайно влепить в скобки два плюса или два минуса. Но тогда это уже будут квадрат суммы и квадрат разности. А это — совсем другие формулы…
Итак:
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.
Переходим к следующей группе формул — к сумме и разности кубов:

Приём для запоминания здесь следующий. В первых скобках (маленьких) знак совпадает со знаком в исходном выражении: плюс-плюс, минус-минус. А вот во вторых (больших) скобках — меняется на противоположный. Причём меняется не перед квадратами, а снова посерединке! Квадраты a2 и b2 — положительные!
Кстати, посмотрите внимательнее на большие скобки в каждой из формул и сравните с формулами квадрата суммы и квадрата разности!
Нашли отличия? Да! В кубах не хватает двойки посерёдке. Именно по этой причине выражения в больших скобках
a2+ab+b2
и
a2-ab+b2
часто называют неполным квадратом суммы/разности.
А теперь можно и шаблонные словесные формулировки из учебников привести:
Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.
Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.
Вот так. Слово "неполный" хорошо помогает не запутаться. Допустим, в тревожной боевой обстановке на контрольной или экзамене нахлынули сомнения — писать двойку в сумме/разности кубов или нет? Вот тут самое время вспомнить, что в кубах стоят неполные квадраты. А для полных квадратов есть свои формулы. Которые к кубам не имеют никакого отношения.
Остаётся последняя парочка — куб суммы и куб разности:

Эти две формулы встречаются в заданиях пореже предыдущих пяти, но знать их тоже не помешает, да. Претендуете на пятёрку? Тогда читаем дальше!
Итак, как запомнить куб суммы? Во-первых, все знаки в формуле — плюсы! Оно и естественно. Ведь мы же перемножаем только положительные выражения, так с какого перепугу минусам-то взяться? Первое и последнее слагаемые — чистые кубы первого и второго выражений. А вот по центру — утроенные произведения.
Обратите внимание, как в формуле идут переменные a и b! Переменная a идёт по убыванию степени — сначала a3, потом a2, потом просто a (т.е. a1), а в последнем слагаемом буква a и вовсе исчезает, превращаясь в единичку или a0. Для полной ясности ситуации последнее слагаемое b3 я перепишу вот так:
b3 = 1∙b3 = a0∙b3
А вот переменная b — наоборот, идёт по возрастанию степени. От нуля и до тройки включительно: в первом слагаемом переменной b нет (т.е. она сидит в виде единички, или b0), во втором b1, в третьем b2, в четвёртом b3.
Но и это ещё не всё! Смотрите-ка, какая интересная штука: сумма степеней a и b в каждом из слагаемых всегда равна трём! Например:
a3 = a3·b0 (3+0=3)
3a2b = 3a2b1 (2+1=3)
и так далее…
Такой порядок хорошо помогает не запутаться.)
Если вы уловили принцип запоминания куба суммы, то куб разности запомнится без проблем. Всё то же самое, только минусы надо правильно расставить. А это очень легко сообразить! Какая переменная у нас с минусом? Правильно, переменная b! Следовательно, в слагаемых, где b стоит в первой степени и в кубе — будет минус. Ибо любой минус в нечётной степени всегда даёт минус. А вот минус в квадрате (b2) даст плюс. И все дела.)
Разумеется, изложенные выше советы — это не жёсткие правила математики. Это просто практические приёмы, помогающие более быстрому и комфортному запоминанию. Чисто для себя. Куда уж лучше, чем механическая зубрёжка, правда?)
Но, как ни крути, самый надёжный способ запомнить эти формулы — решать побольше примеров. Тогда весь этот перечень запомнится очень быстро. Сам собой, можно сказать.
Ну что, потренируемся?)
Примеры на формулы сокращённого умножения.
Начнём с самого простого — с прямого применения формул. Для разминки.)
Преобразовать в многочлен:
(5x+4y)2
Сразу видим квадрат скобок. А в скобках — сумму. Значит, работаем по самой первой формуле, вот этой:
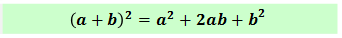
Вспоминаем словесную формулировку: "Квадрат первого выражения…". За первое выражение у нас идёт 5x. Квадрат будет 25х2. Вот и пишем:
(5x+4y)2 = 25х2….
Идём дальше: "Плюс удвоенное произведение первого выражения на второе…". Удвоенное — это умножение на двойку. Первое выражение — это 5x, второе — это 4y. Продолжаем:
(5x+4y)2 = 25х2+2∙5x∙4y….
"Плюс квадрат второго выражения." В роли второго выражения у нас 4y. Квадрат — это 16y2. Получим:
(5x+4y)2 = 25х2+2∙5x∙4y+16y2
Практически всё. Осталось "причесать" удвоенное произведение (перемножить 2∙5∙4) и получим окончательный ответ:
(5x+4y)2 = 25х2+40xy+16y2
Это было разминочное задание. А теперь примерчик посерьёзнее.
Разложить на множители:
4x2–20x+25
Что, внушает? Опять смотрим на наш список. Но не на тот, что в начале урока (для умножения), а на второй, для разложения на множители. Вот на этот:
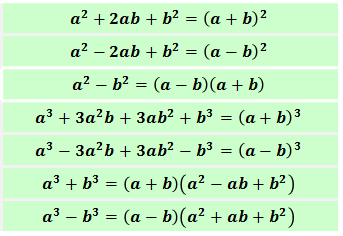
Тут, разумеется, нашего выражения нет. Ну и что? Здесь важно понимать, что под буквами a и b может скрываться всё что угодно — и числа, и другие буквы, и более сложные выражения. Поэтому смотрим на список и ищем похожую формулу. И зацепкой будут степени переменной.
В нашем выражении есть x2 и просто x. Ясное дело, отбрасываем все формулы с кубами — у нас их явно нет. Далее выкидываем из рассмотрения формулу разности квадратов: там нет переменных в первой степени, только квадраты. А у нас — есть.
Остаются первые две формулы — квадрат суммы или квадрат разности. Уже проще, не так ли? Осталось сообразить, что в формуле квадрата суммы — только плюсы. А в нашем выражении в серединке стоит минус. Стало быть, похожая формула — это квадрат разности.
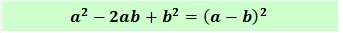
Но не факт, что квадрат разности сработает, совсем не факт… Наша задача — убедиться, что предложенное выражение 4x2–20x+25 точно соответствует квадрату разности. Только тогда у нас появится возможность записать и правую часть равенства (т.е. разложение на множители).
Для удобства я перепишу формулу и исходное выражение прямо одно под другим:
a2-2ab+b2 = (a-b)2
4x2–20x+25 = ….
Надо выяснить, что скрывается под буквами a и b в нашем выражении. Начинаем по порядочку — с самого первого слагаемого. Допустим, a2 — это 4x2. Тогда чему равно само а? Какое выражение в квадрате даёт 4x2? Очевидно, что 2х. Тогда a=2x. Есть! Первое выражение нашли.
А что может скрываться под b2. Ну, точно не 20х! Во-первых, икс уже в букве a сидит, а во-вторых, b2 должно быть с плюсом. А 20х у нас с минусом. Значит, под b2 скрывается число 25! Стало быть, b — это пятёрка!
Итого: a=2x, b=5
Всё? Можно записывать разложение? Пока нет.
Нужна последняя, контрольная проверка по выражению 20х. Надо убедиться, что наши 20х точно соответствуют удвоенному произведению 2ab.
Итак, затаив дыхание составляем удвоенное произведение первого и второго выражений:
2ab = 2∙2x∙5 = 20x
Ура! Совпало! Значит, наше выражение — это действительно квадрат разности 2х и 5. Вот теперь можно со спокойной душой записывать ответ:
4x2–20x+25 = (2х-5)2
Идея ясна? Сначала ищем в списке похожую формулу, а затем сверяем с ней выражение, предложенное в задании, на полное соответствие. Если повезло и всё совпало, то записываем ответ. Если не повезло, то, значит, раскладывать надо как-то иначе.
Это были самые простые примеры, для младшеньких. А теперь переместимся в старшие классы, с их синусами да логарифмами. Да-да, старшеньким формулы сокращённого умножения тоже бывают нужны!
Например, такое задание:
Упростить:
cos4x — 2cos2x∙sin2x + sin4x
Вся мощь тригонометрии слабо помогает в этом примере. Только алгебра седьмого класса и спасает, да…
Конечно, это выражение сильно смахивает на квадрат разности. Вот и пробуем применить эту формулу к нашему выражению! Что будет скрываться под буквами a и b? Конечно же, cos2x и sin2x. Удвоенное произведение, ясен перец, будет 2cos2x∙sin2x, как, собственно, в нашем выражении и записано. Смело сворачиваем нашего монстра в квадрат разности по формуле:
cos4x — 2cos2x∙sin2x + sin4x = (cos2x - sin2x)2
А вот теперь и тригонометрия в игру вступает! Что у нас в скобочках? У нас в скобочках косинус двойного угла!
cos2x - sin2x = cos2x
Вот вам и ответ:
cos4x — 2cos2x∙sin2x + sin4x = cos22x
Или такое задание:
Вычислить:
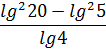
Пример не подарок, прямо скажем… Логарифмические формулы явно не катят, да и сами логарифмы ровно не считаются… Проверим на алгебру? Числитель явно намекает на применение формулы разности квадратов.
Вот этой: a2–b2 = (a-b)(a+b)
В роли a и b у нас логарифмы. Ну и что? Это формулу никак не портит, ибо законы алгебры работают во всей математике. Смело заменяем числитель дроби на произведение скобок и пишем:
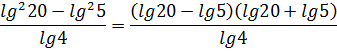
А вот теперь и логарифмические формулы заработали! В первых скобках (разность) получается lg4, который и сокращается благополучно со знаменателем. А во вторых скобках (сумма) будет lg100. Что по свойствам логарифмов есть 2.
Конечно, подобные примеры в этом уроке легко решаются. Но на практике, когда ученик глубоко погружён в синусы/косинусы да логарифмы, разложение на множители просто не приходит в голову…
Посему практический совет:
Проверяем замороченные примеры на алгебру седьмого класса! В частности, на формулы сокращённого умножения.
И напоследок…
О типичном ляпе, который сразу же показывает блистательное отсутствие хоть какого-то понимания. Ляп настолько часто встречается, что хочется заявить громко:
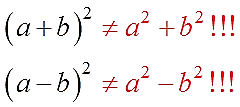
И запомните это крепко-накрепко!
Формулы — штука жёсткая! Раз требуют удвоенного произведения 2ab, помимо чистых квадратов, значит спорить бессмысленно. Напишете такое на контрольной — будьте готовы получить заслуженную двойку! Такого не прощают. Вот так.
Наглядный пример на добрую память с квадратом суммы. Всё-таки картинки иногда проливают свет на очень многие волнующие вопросы. Нарисуем в тетрадке квадрат со стороной a+b. Можно по клеточкам. Допустим, для конкретики, a — это 4 клетки, a b — это 2 клетки.
Вот так:
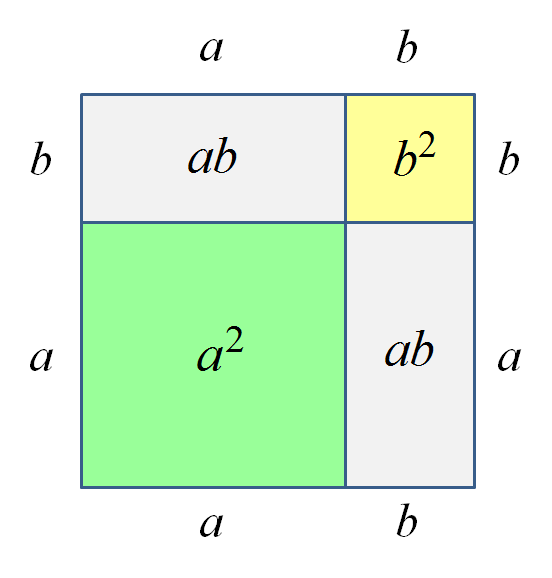
Очевидно, площадь всего квадрата будет равна квадрату его стороны, т.е. как раз (a+b)2. В числах, безо всяких формул, это будет (4+2)2 = 62 = 36.
А теперь, глядя на картинку, соображаем: из чего складывается эта площадь? Правильно! Из большого (зелёного) квадрата площадью a2, маленького (жёлтого) квадратика площадью b2 и двух прямоугольников по ab площадью каждый.
Вот и получается: (a+b)2 = a2+ab+ab+b2 = a2+2ab+b2
Или, в числах, для a=4 и b=2:
(a+b)2 = a2+2ab+b2= 42+2∙4∙2+22 = 16+16+4 = 36
Вот и все дела.)
Упражнение для интересующихся: аналогичным образом доказать геометрически (т.е. через квадраты и прямоугольники) две другие формулы сокращённого умножения с квадратами — квадрат разности и разность квадратов. Попробуйте! Интересно.)
Ну что, порешаем?)
1. Преобразовать в многочлен стандартного вида:
(5a+1)2=
(3y-4)2=
(a-y3)2=
(a2+b2)2=
(3b-1)(3b+1)=
(x+7)(7-x)=
(3x+2)3=
Ответы (в беспорядке):
9b2 — 1
9y2-24y+16
27x3+18x2+36x+8
a4+2a2b2+b4
25a2+10a+1
49-x2
a2-2ay3+y6
Ну как, размялись? Получилось? Тогда продолжаем:
Разложить на множители:
16x2+8x+1 =
36x2y4-60xy2+25=
y2-100=
81a2-64x2y6=
27m3+8=
64x3-y6=
Ответы (в беспорядке):
(y-10)(y+10)
(4x-y2)(16x2+4xy2+y4)
(4x+1)2
(9a-8xy3)(9a+8xy3)
(6xy2-5)2
(3m+2)(9m2-6m+4)
И это получилось? Блеск! Значит, формулы сокращённого умножения на самом минимально необходимом уровне вы освоили. Можно браться за задания посерьёзнее.
Что-то не срослось? Бывает… Возможно, проблема не в самих формулах, а в банальной арифметике — знаках, действиях со степенями. Повторите степени! Без отточенного навыка работы со степенями дальше идти нельзя. К сожалению…
А вообще, рецепт здесь простой — решать побольше заданий! Да-да! Задания этого урока — капля в море. Помогут, но не сильно. Маловато их… Берите любой учебник 7-го класса и решайте, решайте! До автоматизма. А сайт — ваш надёжный помощник! Тогда формулы сами собой и запомнятся. А труды окупятся. Проверено!)
