Этот урок является продолжением предыдущего урока "Метод интегрирования по частям — основы". Там мы познакомились с общей идеей самого метода и порешали примеры на произведение многочлена и показательной/тригонометрической функции. Напоминаю, что такие интегралы относились к первой группе нашей сводной таблички.
Вот этой:
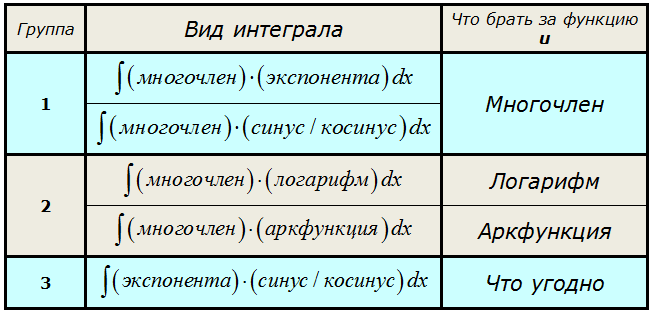
В этом уроке переходим ко второй группе интегралов, к произведению многочлена и логарифмической / обратной тригонометрической функции.
Итак.
Как интегрировать логарифмы, арки и прочие ужасы?
Например:

И тому подобные примеры.
Общее правило здесь следующее:
Если под интегралом присутствует логарифм или арк, то именно его выбираем в качестве функции u. Всё оставшееся принимаем за dv.
Общая схема выглядит так:
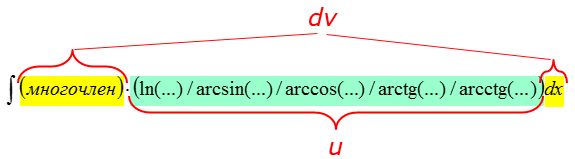
Почему именно такой выбор следует делать? А вот почему.
Напоминаю, что разделение разнотипных функций под интегралом и упрощение исходного примера через вспомогательные функции u и v (дифференцирование функции u и интегрирование множителя dv) — это ключевая идея метода интегрирования по частям.
Что происходило в интегралах первой группы (произведение многочлена на показательную/тригонометрическую функцию)? Там за функцию u всегда принимался многочлен. По той простой причине, что именно дифференцирование многочлена превращало исходный пример если не в белый и пушистый, то хотя бы делало его проще. А именно — за счёт понижения степени многочлена.
С логарифмами/арками в этом уроке та же фишка, что и с понижением степеней многочленов в прошлом: производные от логарифмов и арков — куда более простые конструкции, чем сами логарифмы/арки! Не верите? Вспоминаем таблицу производных:
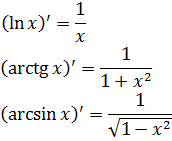
И так далее.
Как мы видим, после их дифференцирования получаются либо дробно-рациональные функции, либо (в худшем случае) выражения с радикалами (корни из квадратных трёхчленов). Т.е. если продифференцировать логарифм/арк — не будет ни логарифма, ни арка. Интеграл упростится! Именно в этом вся суть.)
Казалось бы, какая разница, что там сидит под интегралом — логарифм или дробь какая-то… Хрен редьки не слаще.
Ошибаетесь! Разница очень существенная. С точки зрения интегрирования алгебраические функции (т.е. многочлены, рациональные дроби, радикалы и их сочетания) куда проще всех остальных! Где-то можно вообще сработать по таблице, где-то элементарно преобразовать по школьной формуле, где-то что-то заменить, упростить и т.д… Далеко не всегда, разумеется, всё от конкретного выражения зависит. Но в целом для операции интегрирования такие функции (где только многочлены, степени, дроби и нету тригонометрии, логарифмов и показательных выражений) — самые удобные.
А вот логарифмы с арками для их интегрирования "с нуля" — довольно скверные товарищи. Базовые приёмы интегрирования (тождественные преобразования, подведение под знак дифференциала, замена переменной) против них бессильны. И таблица не спасает. Нету для логарифмов/арков готовых табличных формул… Нет, в природе, сами по себе, эти формулы есть, вообще-то. Но… слишком сложные. На конкретных примерах сами увидите.
Пора переходить к этим самым конкретным примерам. Разбираем первый пример по списку. Пока подробно, остальные — более кратко.
Найти неопределённый интеграл:
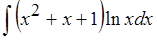
Под интегралом сидит произведение многочлена и логарифма. Не очень удачное сочетание, да…) Хотелось бы чего-то попроще, правда? Многочлен — сам по себе простая (для интегрирования) функция, а вот от логарифма не помешало бы избавиться… Но как? Замена и прочие типовые приёмы не работают. Остаётся единственный законный способ убрать логарифм — продифференцировать его. Работаем по формуле интегрирования по частям и разбиваем функцию на кусочки. Вспоминаем алгоритм!
Внимательно осматриваем подынтегральную функцию и определяем (по таблице), к какой группе относится данный интеграл. Разбиваем подынтегральное выражение на две части (u и dv), согласно правилу именно для данной группы.
У нас вторая группа. Разбиваем согласно правилу для второй группы: lnx — это u, а многочлен вкупе с dx, т.е. (x2+x+1)dx — это dv.
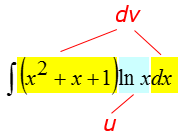
Так и пишем:
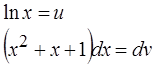
Для запуска формулы не хватает du и v. Не вопрос!
Дифференцируем u (т.е. логарифм), получаем du:
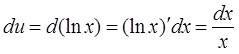
Интегрируем dv и получаем v:
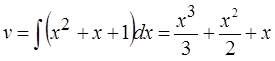
Вот и славно. Функция v — обыкновенный многочлен, а du — совсем простая конструкция dx/x. Не логарифм, чай.) Жизнь налаживается!
Подставляем исходные данные в формулу интегрирования по частям:
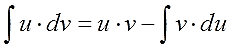
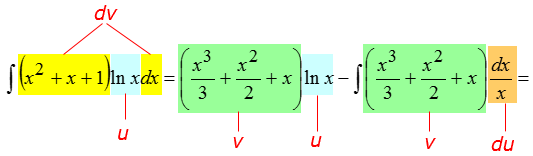
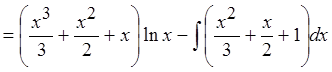
Вот теперь сразу всё видно. Мешающий нам логарифм после дифференцирования исчез из примера. Под новым интегралом получился многочлен, куда более простая для интегрирования конструкция! Решать пример стало одно удовольствие.) Интегрируем этот многочлен:
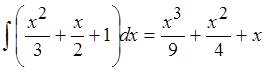
Проблемы? Тогда вам сюда. Напоминаю, что любые многочлены на данном уровне вы должны уметь интегрировать на автомате. С любыми степенями, знаками и коэффициентами. И без ошибок.
Осталось всего ничего. Вставляем полученный многочлен, результат промежуточного интегрирования, на своё место, раскрываем скобки, прибавляем константу С и окончательно записываем:
Ответ:
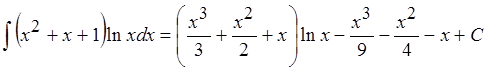
Вот и всё.) Желающие могут взять производную от ответа и получить исходную функцию (x2+x+1)lnx. Я продифференцировал. И вы попробуйте! Полезная самопроверка.)
Переходим к следующему примеру. Пример совсем простой, но в тупик некоторых ставит, да…)
Проинтегрировать функцию:
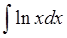
Как обычно, шагаем по алгоритму:
Разбиваем подынтегральное выражение на две части (u и dv), согласно правилу для второй группы.
Отличие от предыдущего примера в том, что в этот раз под интегралом сидит одинокий логарифм, а многочлен как таковой блистательно отсутствует. Это и смущает поначалу. Как разбивать на u и dv?
Не вопрос. Точно так же! Очевидно, что логарифм lnx — это u. А что же тогда dv? Да то что осталось, то и будет dv! Что, вам кажется, что ничего не осталось? Ничего подобного! Невыбранным у нас осталось dx.
Вот и пишем:
dv = dx
Да-да, именно так.)
Строго говоря, многочлен перед логарифмом присутствует и в этом примере. Просто многочлен этот равен… единичке.) Ведь подынтегральную функцию можно переписать и вот так:
lnx = 1·lnx
Имеем полное право. А многочлен с одним лишь членом (единичкой) — тоже многочлен, да.) Только без иксов. Так бывает.)
Я даже не поленюсь и припишу эту единичку множителем под самим интегралом. Тогда схема выбора u и dv будет следующей:
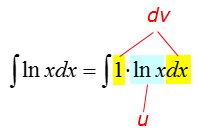
А дальше — по проторенной дорожке. Вместо старого интеграла ∫u·dv формируем новый интеграл ∫v·du, который будем брать вместо исходного. Для этого ищем v и du:
Интегрируем dv и получаем v:
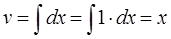
Дифференцируем u, получаем du:
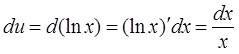
Подставляем исходные данные в формулу интегрирования по частям:
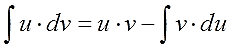
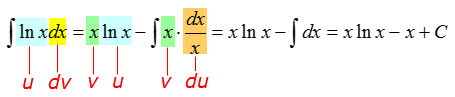
Ответ:
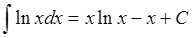
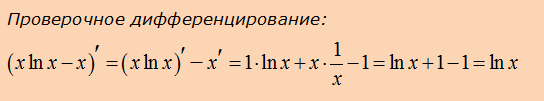
Вот и всё.) Как видите, с логарифмами нет ничего сложного. Убираем логарифм дифференцированием и сводим интеграл к степенной конструкции (чаще всего, многочлену).
Между прочим, на натуральном логарифме ln свет клином вовсе не сошёлся.) Вполне может попасться и что-то "школьное" типа lgx или log3x и т.п. Как поступаем с ненатуральными логарифмами? Очень просто! По формуле перехода к новому основанию превращаем их в натуральные! Вот так:
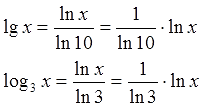
И т.п.
А дальше — как с привычными натуральными логарифмами. Да, кстати… Надеюсь, вы понимаете, что дроби 1/ln10, 1/ln3 и т.п. — это просто обычные константы? Вот и работаем с ними как с константами (выносим за знаки производной/интеграла и т.п.).
Разбираемся с арками.)
Например:
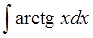
Примеры с арками лишь немногим сложнее примеров с логарифмами. По той причине, что производные арков — чуть более хитрые выражения, чем 1/х. Но суть та же самая — убрать арк при помощи дифференцирования и получить более простую функцию под интегралом. В нашем случае будем избавляться от арктангенса. Т.е. принимаем u=arctgx.
Сразу пишем:
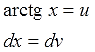
Находим v и du:
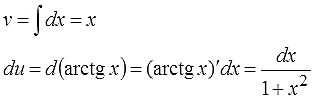
Подставляем исходные данные в формулу интегрирования по частям:
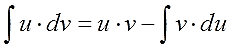
Надеюсь, художества в виде подробных подписей со стрелочками уже не требуются? Разберётесь поди?)
Расписываем по формуле:
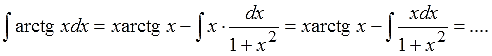
Вот всё и наладилось! Арктангенс благополучно исчез, и пример свёлся к интегрированию более простой функции — рациональной дроби x/(1+x2). А с такой дробью мы уже давно знаем, что делать! Интегрируем эту дробь методом подведения знаменателя под знак дифференциала.
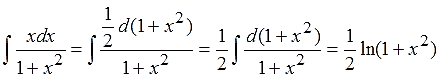
Опять проблемы? Ну, так интегрирование по частям не отменяет всех остальных правил интегрирования, да…) Подведение под знак d, замена переменной и т.п. Ходите по ссылочкам, там вся интересующая вас информация.
А мы вставляем результат на место, прибавляем пресловутую С и записываем:
Ответ:
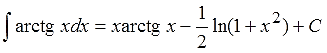
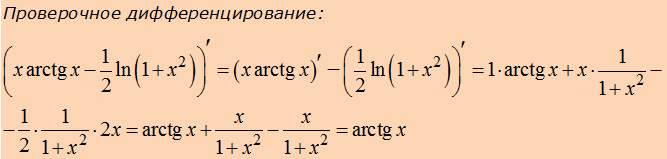
Ну как, понравилось? Ещё бы! Приятно ведь, когда арки исчезают, правда?) Тогда вот вам примерчик для самостоятельного решения. Поразвлекайтесь с арксинусом:
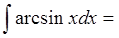
Ответ:
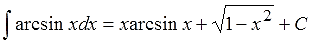
Получилось?) Проверили ответ дифференцированием? Отлично!
Обратите внимание! Несмотря на то, что логарифмы с арками относятся к элементарным "школьным" функциям, их первообразные (не путать с производными!) — далеко не простенькие табличные функции. А довольно-таки хитрые выражения! Судите сами:
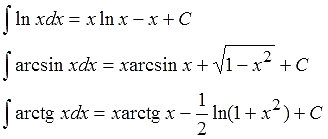
И т.д…
Будете зубрить? Правильно, не будете. И не надо.) Именно по этой причине функции lnx, arcsinx, …, arcctgx и отсутствуют в стандартной таблице интегралов. Эти интегралы — не табличные. Посему запоминать все эти длинные выражения с корнями и логарифмами, разумеется, не нужно. Но понимать, что логарифмы и арки интегрируются по частям — крайне важно.
Что ж, растём дальше. Продолжим развлекаться и добавим какой-нибудь икс в степени n (т.е. многочлен).
Типа такого монстра:
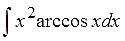
По сравнению с предыдущими примерами, икс в квадрате перед арккосинусом здорово осложняет жизнь, да… Но пугаться не стоит. Как обычно, с чувством, с толком, с расстановкой, работаем себе по алгоритму. Вместе со мной. Ну а я, комментируя промежуточные выкладки, помогу вам не утерять нить рассуждений и не запутаться. Итак, поехали!
Первый шаг до ужаса простой и привычный. Убираем арккосинус дифференцированием.
Вводим обозначения u и dv в соответствии с правилом:
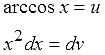
Находим v и du:
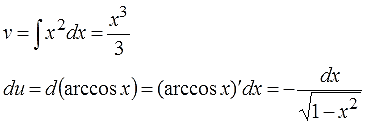
Надеюсь, формулу производной арккосинуса помнят все? Да. Это производная арксинуса, только взятая со знаком минус.
Аккуратно подставляем все данные в формулу интегрирования по частям:
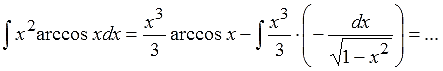
Приводим новый интеграл ∫vdu к приличному виду и берём его:
Итак, упрощаем новую подынтегральную функцию: уводим x3 в числитель дроби, а константу 1/3 вместе с минусом выносим за знак интеграла. Получится:
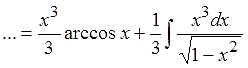
Ну всё, пора интегрировать. И снова подынтегральная функция свелась к более простому выражению, чем арккосинус. Сомневаетесь? Корень пугает? Зря. В нашем примере от него очень легко избавиться. Подведение функции под знак дифференциала и замена переменой — мощные штуки!
Вот и упрощаем дальше до упора. Упрощать будем в два шага. Первым шагом подводим под знак d выражение x2 и сразу же вводим замену t=x2.
Как подводим? Легко! Берём числитель x3 и нагло "отщипываем" один икс, т.е. раскладываем числитель на две степени — x2 и x. А икс есть не что иное, как производная квадрата, ибо 2x=(x2)’ ! Что вообще великолепно. Получится:
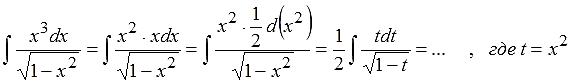
Отлично. Процесс идёт.) Буква t помогла нам убрать все квадраты. Но корень — нет. Тупик? Отнюдь! Переходим к шагу №2. Ликвидируем корень с помощью введения ещё одной замены. Степенной. Поскольку мешающий нам корень — квадратный, обозначаем всё подкоренное выражение как квадрат новой переменной. Например, z. Да, прошу обратить внимание, заменяем не просто t, а всё подкоренное выражение целиком!
Вот так:
1-t=z2,
откуда, выражая t и dt через z, получится:
t=1-z2 и dt=d(1-z2)=-2zdz
Разумеется, корень из всего выражения 1-t (в знаменателе) окажется равен просто z. Раз уж сама разность 1-t — это z2.
Заменяем:
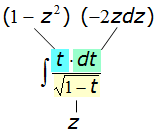
Тогда, после новой замены, буква z в знаменателе сократится, и под интегралом получится… получится… многочлен! Ура! Никаких корней, никаких дробей.)
Продолжаем выкладки, уже с новой буквой z:
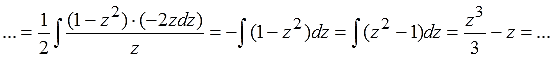
И все дела.)
Напоминаю, что последовательно заменять переменную интегрирования можно сколько угодно раз. До тех пор, пока подынтегральная функция не упростится настолько, что вам уже станет всё ясно. Разумеется, после получения конечного результата не забываем возвращаться обратно к старым переменным!
Вот и возвращаемся — от z к t, а от t — к иксу.
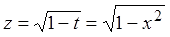
И переписываем результат в старых буквах:
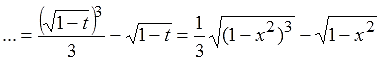
А вот сейчас самое главное — вспомнить, чего мы ищем-то… А то, в трудах тяжких, можно и позабыть чего-то, да.)
А ищем мы, напоминаю, новый интеграл от выражения vdu, т.е. ∫vdu.
Вот такой он получился:
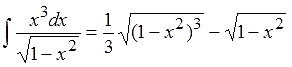
Почти готово. Остались пустяки — подставить полученное выражение в формулу интегрирования по частям (т.е. просто помножить на +1/3) да добавить заветную буковку С.
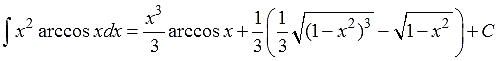
Упрощаем (для красоты), записываем окончательный ответ:
Ответ:
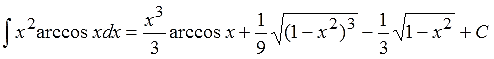
Однако… Нехилая работа понадобились. Хотя в общем-то тривиальная. Для опытных.)
Логарифм или арк стоит в степени — как быть?
Речь здесь пойдёт только о натуральных показателях n (2, 3, 4, и т.д.). Такие примеры — самые злые, да…) Но всё-таки иногда встречаются.
Например:
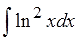
Под интегралом не просто логарифм, а в квадрате. Что делать? В подобных примерах необходимо последовательно понижать степень логарифма (арка). Разумеется, через дифференцирование. На единичку с каждым новым шагом. До тех пор, пока на n-ном шаге логарифм (арк) не исчезнет полностью. Собственно, злость этих примеров заключается в том, что такое последовательное понижение степени приводит к необходимости n-кратного интегрирования по частям. Самое главное здесь — внимательно следить за каждым шагом, дабы не запутаться в выкладках.
Вот и начнём. Т.к. исходная степень логарифма — вторая, то интегрировать будем в два шага. Первым делом убираем квадрат у логарифма (шаг №1).
Обозначаем:
u = ln2x
dv=dx
Дальше всё шаблонно, без фокусов.
Интегрируем dv и получаем v. Дифференцируем u, получаем du.
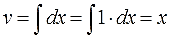
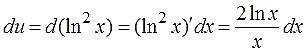
Надеюсь, всем понятно происхождение икса в знаменателе дроби и то, что ln2x — сложная функция?
Подставляем исходные данные в формулу интегрирования по частям:
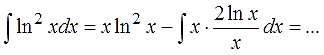
Приводим к приличному виду (сокращаем иксы, выносим двойку за знак интеграла):
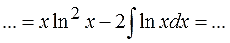
А вот теперь — самое главное! Мы видим, что после первого шага под новым интегралом у нас опять вылез логарифм. Но уже в первой степени вместо второй, что гораздо проще.
Теперь наша задача (шаг №2) — повторным дифференцированием окончательно добить этот логарифм. Ничего не поделать, придётся запускать формулу интегрирования по частям ещё раз, уже только для этого нового интеграла отдельно.
Вот и работаем. Выходим на второй круг.) Теперь за u у нас идёт логарифм lnx, за dv — разумеется, dx. И так далее. В общем, вы поняли.)
Одиночный логарифм мы с вами уже интегрировали выше. Получили вот такой результат:
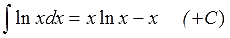
Разумеется, здесь я сразу воспользуюсь этим готовым результатом и дублировать одни и те же выкладки не буду.) Кому непонятно, рекомендую вернуться к примеру с логарифмом и перечитать.
Возвращаемся к шагу №1. Подставляем этот результат на место интеграла от логарифма и прибавляем константу:
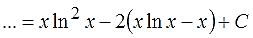
Почти всё. Приводим к приличному виду (раскрываем скобки) и записываем окончательный ответ.
Ответ:

Готово!
Запоминаем:
Если логарифм (арк) стоит в степени n, то интегрирование осуществляется ровно в n шагов. На каждом новом шаге понижаем дифференцированием степень логарифма (арка) на единицу и последовательно интегрируем по частям n раз.
Ну что, прониклись? Ещё бы!) Это ещё цветочки. Растём дальше и переходим к ягодкам. Разбираем ещё более злые примеры. В следующей теме.
